Difference between revisions of "Getting started with MATLAB or Python"
| Line 156: | Line 156: | ||
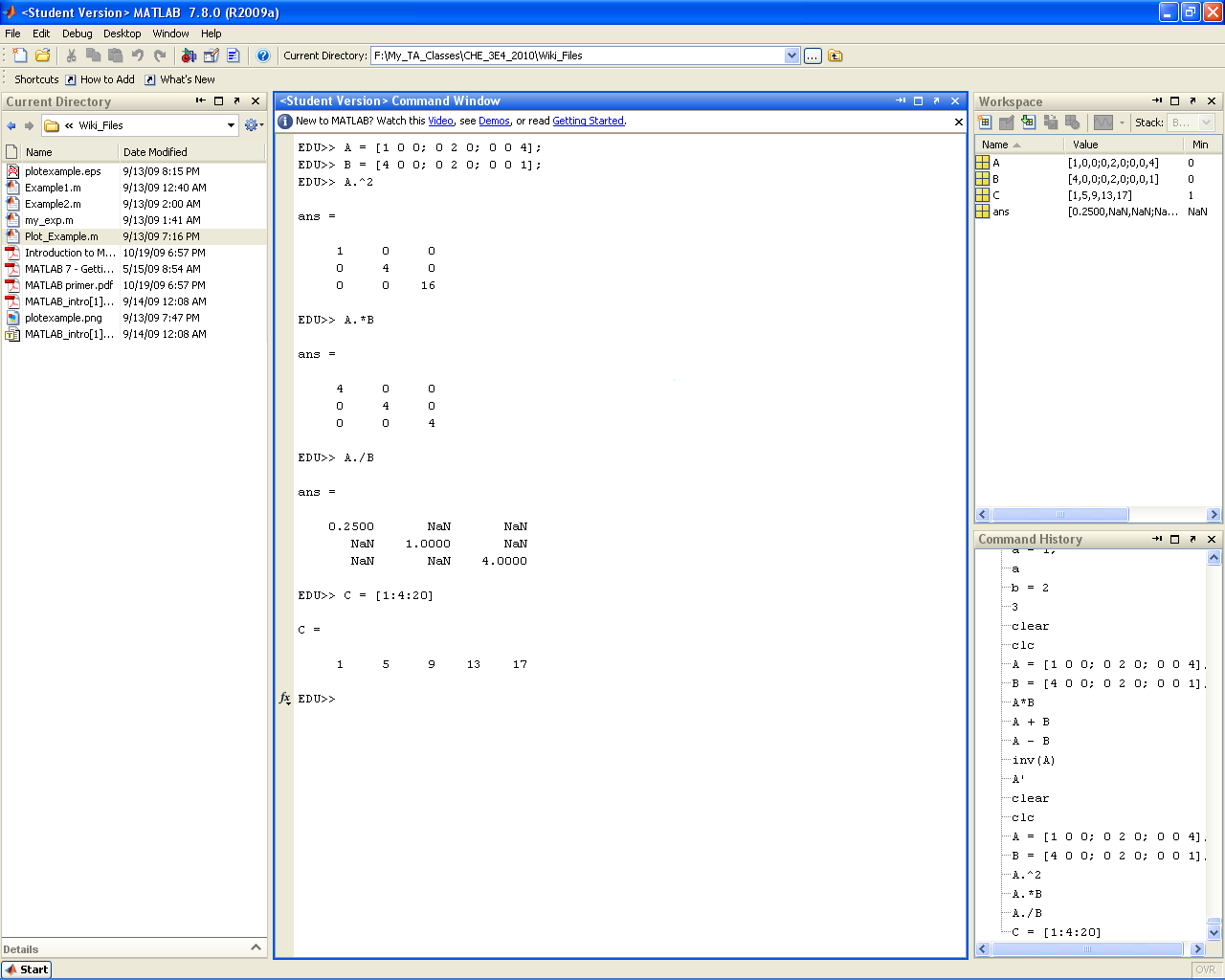
'''Note''': that we must use <tt>.^</tt> to calculate the exponent. If you just write <tt>^</tt> by itself, MATLAB will assume you want to calculate the matrix exponent, which is defined quite differently. In fact, any '''element-by-element''' calculation must use the "." notation to tell MATLAB ''not'' to use its default '''matrix''' calculations. | '''Note''': that we must use <tt>.^</tt> to calculate the exponent. If you just write <tt>^</tt> by itself, MATLAB will assume you want to calculate the matrix exponent, which is defined quite differently. In fact, any '''element-by-element''' calculation must use the "." notation to tell MATLAB ''not'' to use its default '''matrix''' calculations. | ||
For example, use <tt>.*</tt> for element-by-element matrix multiplication. | For example, use <tt>.*</tt> for element-by-element matrix multiplication. If you are bit rusty on this concept, we recommend you read page 4 and 5 of [[Media:MATLAB_primer.pdf | Dr. Mhaskar's Python primer]]. | ||
| width="50%" valign="top" | | | width="50%" valign="top" | | ||
Revision as of 18:56, 12 September 2010
Introduction
| MATLAB | Python |
|---|---|
|
MATLAB (MATrix LABoratory) is a high level computer language/ interactive software package developed and distributed by MathWorks™. Matlab was first developed in the 1970s by Cleve Molar. Cleve was later joined by John N. Little and Steve Bangert and the three went on to found MathWorks™. MATLAB excels at performing matrix operations and can handle large data sets (stored as matrices) very easily. MATLAB was originally designed as a user friendly interface for LINPACK and EISPACK and so was intended for linear algebra application. Since then MATLAB has greatly expanded it's core abilities to encompass a large array of graphic and numeric applications. These core abilities may in turn be expanded further through the addition of specialized "tool boxes". |
From Wikipedia: Python is a high-level programming language whose design philosophy emphasizes code readability. Python aims to combine "remarkable power with very clear syntax", and its standard library of built-in functions is large and comprehensive. We will use the NumPy and SciPy modules (the equivalent of a MATLAB toolbox), to provide scientific computing capabilities to Python. These modules, like MATLAB, allow you to handle large data arrays with little effort. They provide all the tools we require for this course. We will also use the matplotlib module, which provides Python with plotting capabilities similar to MATLAB. |
Access / Installation
| MATLAB | Python |
|---|---|
|
MATLAB is installed on all computers in the John Hodgins Engineering Student Technology Centre (JHE 233A / 234) as well as the Burke Science Building Labs (BSB 241 / 242 / 244 / 249). The most up to date release of MATLAB is version R2010b. While there are some backward compatibility issues when it comes to older versions of MATLAB, for the level of code that will be encountered in this class students should not encounter issues with portability of code. A MATLAB/SIMULINK student package (version R2010A, good for Windows, Mac, and Linux) is available at the University Book Store for $112.95 (for those students who would like a copy of MATLAB on their laptop or home PC). The student versions comes with the following features:
I personally have a student copy on my home PC. It's a good buy if you have the extra cash. |
Python is freely available. The latest stable version that we recommend for the course is version 2.6, because it is compatible with the external libraries that we will use. Installation instructions for Python are available on this website. |
Getting started
These descriptions are specific to Windows-users. Mac and Linux users will have a similar display.
| MATLAB | Python |
|---|---|
|
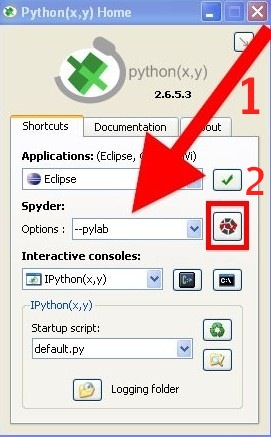
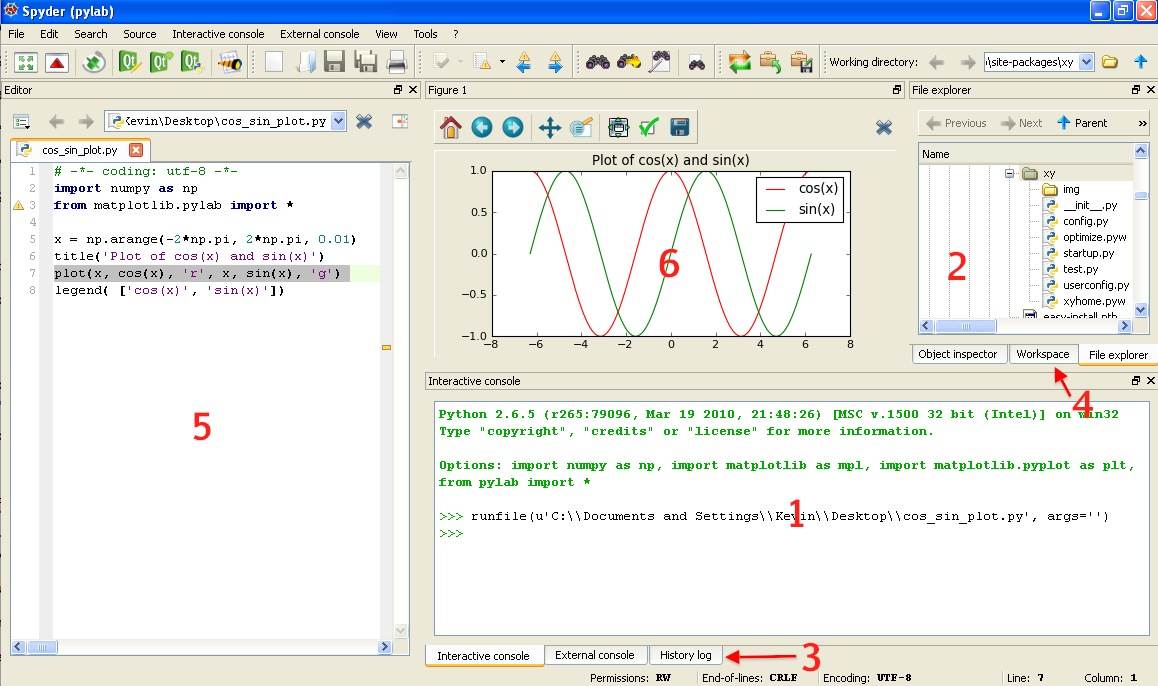
When starting Python(x,y) you will be presented with the following window. Spyder (Scientific PYthon Development EnviRonment) is the name of the development environment we will be using.
You can have one or multiple files open at any time.
|
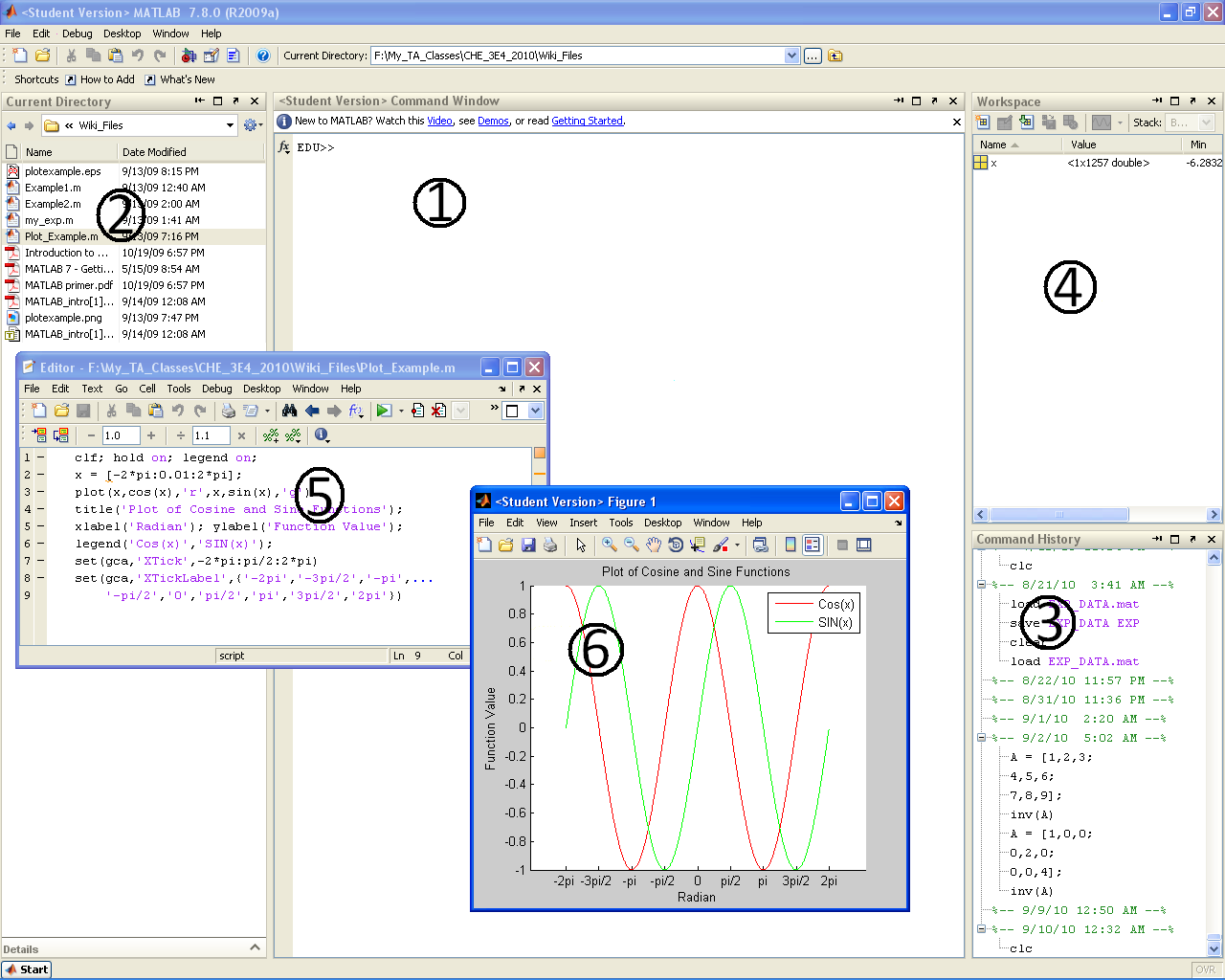
Your first script
In this script we will create a plot with 10 points (a vector), consisting of the numbers
| MATLAB | Python |
|---|---|
|
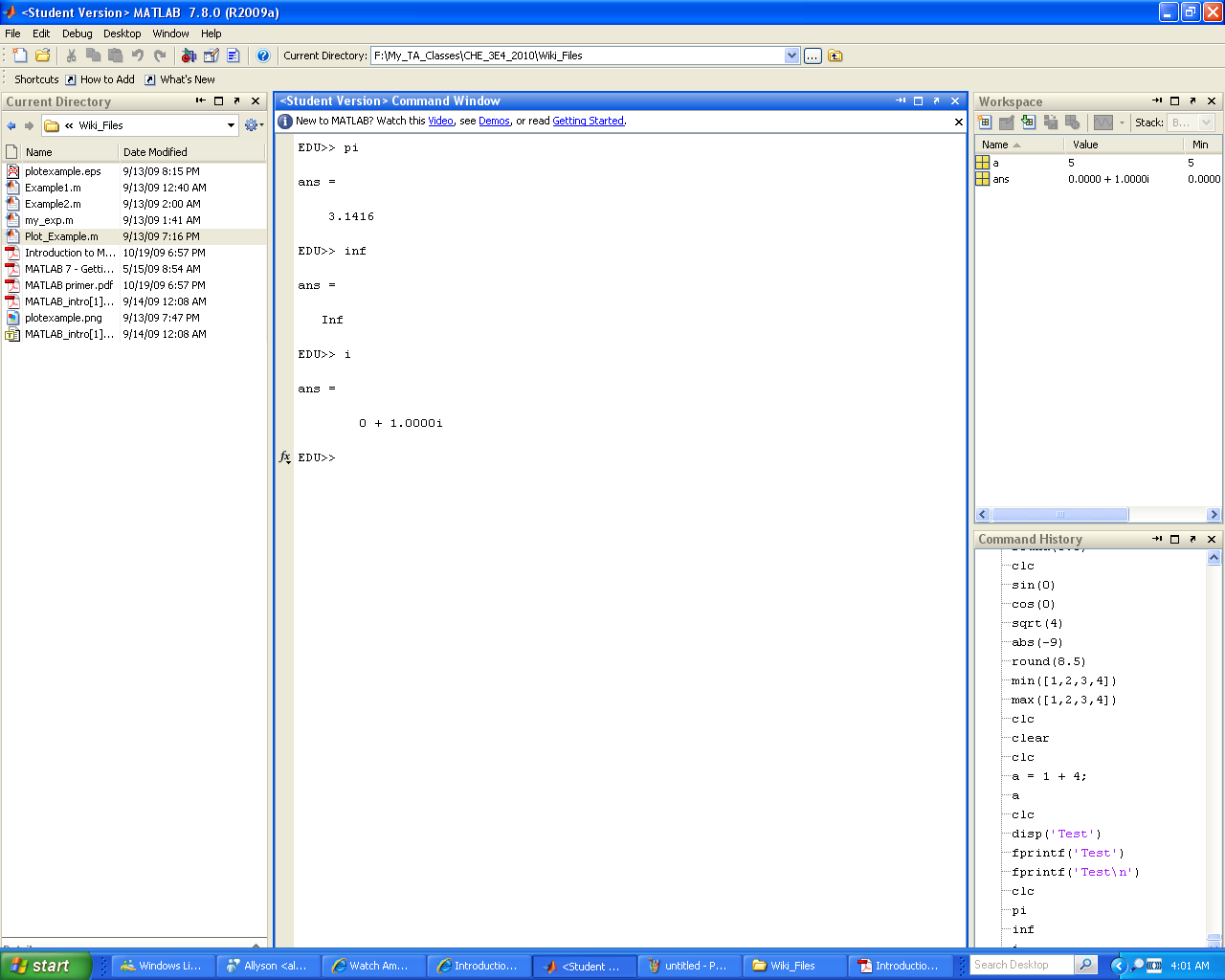
There are several ways we can create our vector >> x = [0 2 4 6 8 10 12 14 16 18];
>> x = [0, 2, 4, 6, 8, 10, 12, 14, 16, 18];
>> x = linspace(0, 18, 10); % easiest method
>> x
x =
0 2 4 6 8 10 12 14 16 18
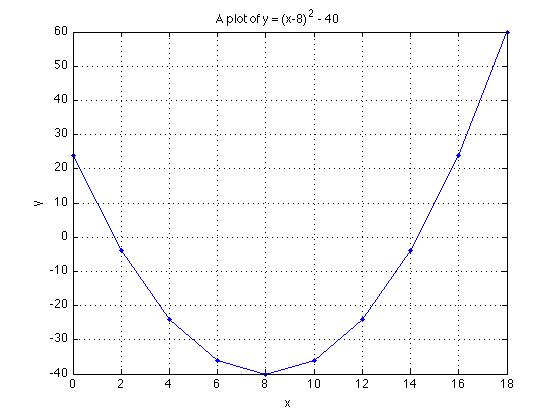
Now create the corresponding >> y = (x-8).^2 - 40;
>> y
y =
24 -4 -24 -36 -40 -36 -24 -4 24 60
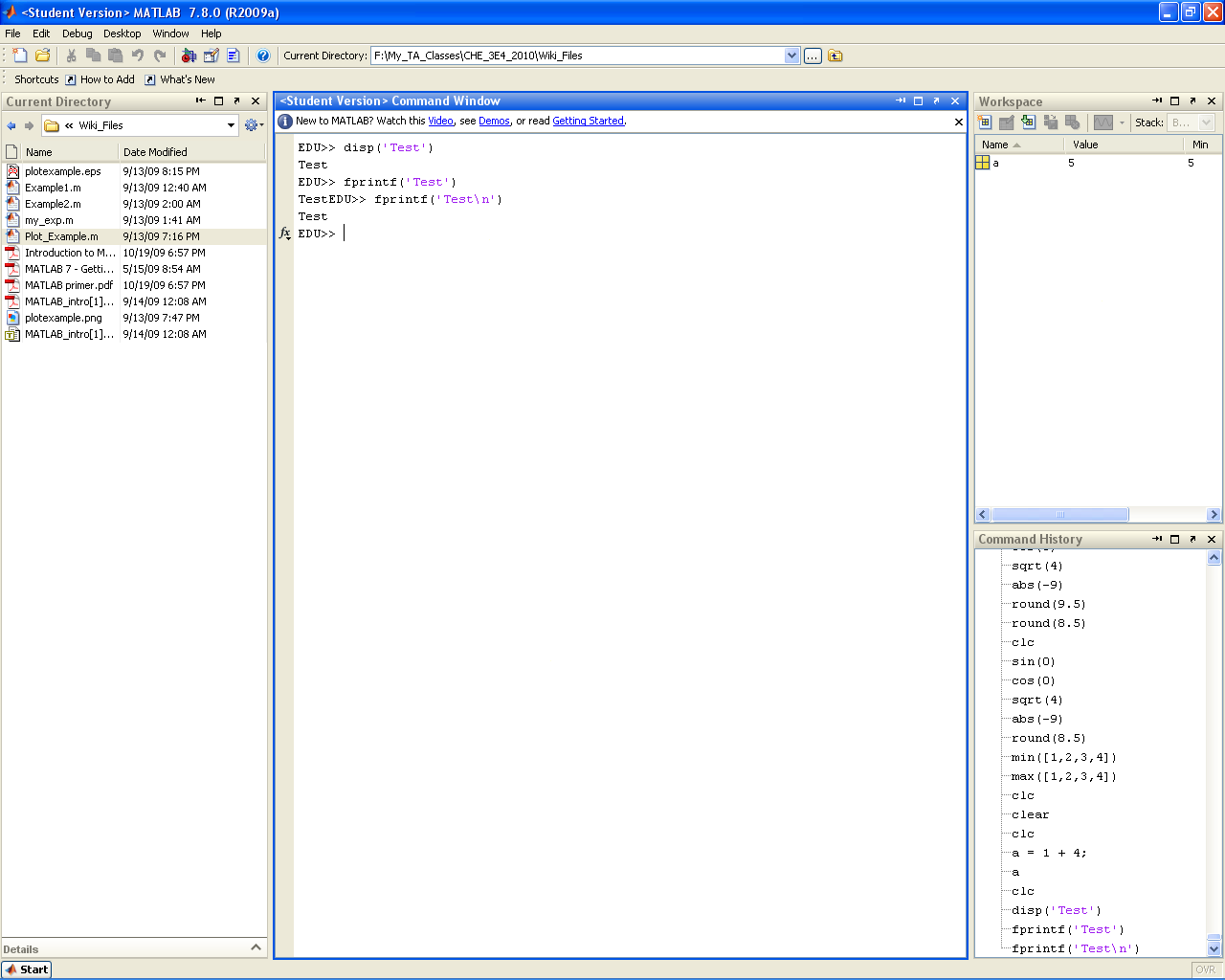
Note: that we must use .^ to calculate the exponent. If you just write ^ by itself, MATLAB will assume you want to calculate the matrix exponent, which is defined quite differently. In fact, any element-by-element calculation must use the "." notation to tell MATLAB not to use its default matrix calculations. For example, use .* for element-by-element matrix multiplication. If you are bit rusty on this concept, we recommend you read page 4 and 5 of Dr. Mhaskar's Python primer. |
There are several ways we can create our vector import numpy as np
from matlabplotlib.pylab import *
>>> x = np.array([0, 2, 4, 6, 8, 10, 12, 14, 16, 18])
>>> x = np.linspace(0, 18, 10) # easiest method
>>> x
array([ 0, 2, 4, 6, 8, 10, 12, 14, 16, 18])
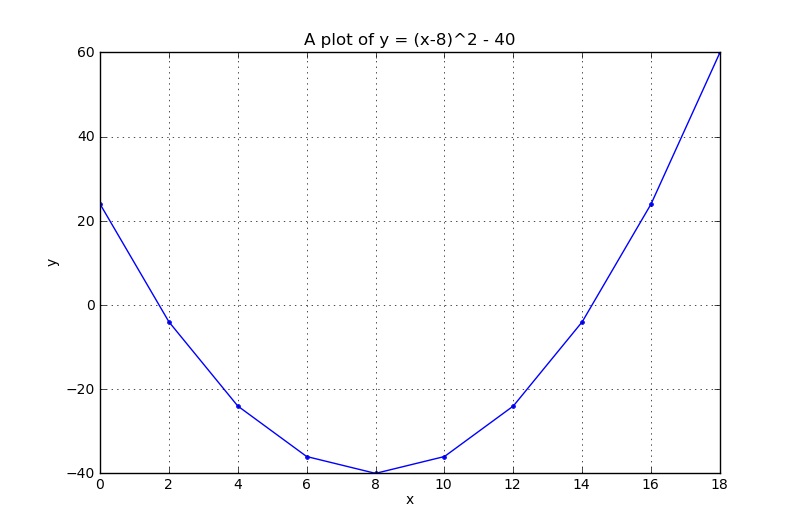
Now create the corresponding >>> y = (x-8) ** 2 - 40
>>> y
array([ 24., -4., -24., -36., -40., -36., -24., -4., 24., 60.])
We raise a variable to a power using the ** notation; the ^ operator means something else in Python. |
Key difference
- In MATLAB, everything is a matrix calculation, by default.
- In Python's NumPy library (numpy), everything is an element-by-element calculation, by default.
Finally, we are ready to plot these
| MATLAB | Python |
|---|---|
plot(x, y, '.-')
grid on
xlabel('x')
ylabel('y')
title('A plot of y = (x-8)^2 - 40')
|
plot(x, y, '.-')
grid('on') # <--- it is a function in Python, so add ()
xlabel('x')
ylabel('y')
title('A plot of y = (x-8)^2 - 40')
|
Introduction to the Command Line
|
|
Scripts and Functions
|
|
Code Structures
|
|
Plotting Data
|
|
Additional Resources
|
|