Software for integrating ODEs
Example
Consider the pair of differential equations (covered in a class on 11 February): <rst> <rst-options: 'toc' = False/> <rst-options: 'reset-figures' = False/> .. math::
\dfrac{dX}{dW} &= \dfrac{-r_A'}{F_{A0}} \\ \dfrac{dy}{dW} &= -\dfrac{\alpha}{2y}\left(1 + \varepsilon X\right)
Some terminology (recap from your pre-requisite math courses)
* The independent variable is \(W\) * The two dependent variables (variables being integrated with respect to the independent variable) are \(X\) and \(y\)
Since there are two dependent variables, we require initial conditions for each variable. In this case:
* :math:`X(0) = 0.0` * :math:`y(0) = 1.0`
We also need to specify initial **and final conditions** for the independent variable:
* :math:`W` initially is 0.0 at the reactor entrance * :math:`W` finally is 20.0 kg at the reactor exit
But there are a few other unknowns we must first specify:
* :math:`r_A' = -k' \dfrac{(1-X)y}{(1+\varepsilon*X)}` * :math:`q = \dfrac{(1 + \varepsilon X)}{y}` * :math:`F_{A0} = 0.1362\,\text{mol.s}^{-1}` * :math:`k' = 0.0074\,\text{mol.s}^{-1}\text{.(kg catalyst)}^{-1}` * :math:`\alpha = 0.0367\,\text{kg}^{-1}` * :math:`\varepsilon = -0.15` </rst>
Polymath
Download and install Polymath from the CD/DVD included with your course textbook (Windows only; sorry Mac and Linux versions are not available). Unfortunately this is only a 15 day version, which is pretty useless for this course, since you will require the code for at least the next 30 to 45 days. So rather use one of the other options below, if possible.
Enter the following Polymath code (as demonstrated in class on 11 February. Check the video out for a detailed explanation of the code.
# Differential equations
d(y) / d(W) = -alpha/(2*y) * (1+eps*X)
y(0) = 1.0
d(X) / d(W) = -rAdash / FA0
X(0) = 0
# Constants
FA0 = 0.1362 # [mol/s]
kdash = 0.0074 # [mol/(kg catalyst . s)]
alpha = 0.0367 # [1/kg]
eps = -0.15 # [-]
# Algebraic equations
rAdash = -kdash * (1-X)/(1+eps*X) * y
flow_ratio = (1 + eps*X)/y
# Initial and final values for independent variable:
W(0) = 0
W(f) = 28
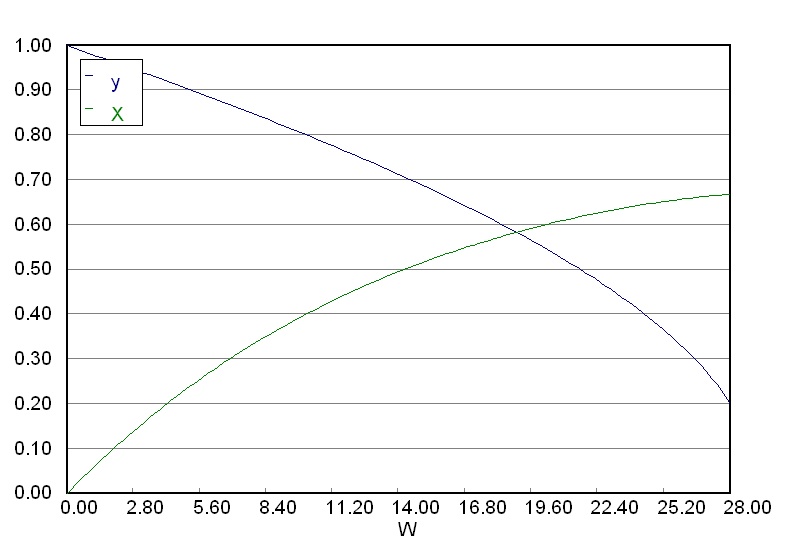
Ensure that you obtain a graphical output as shown here. This represents the profile of conversion, \(X\) and the pressure drop ratio \(y\) throughout the reactor.