Difference between revisions of "Mixed-Integer linear programming"
Kevin Dunn (talk | contribs) |
Kevin Dunn (talk | contribs) |
||
| (24 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
{{ | {{ClassSidebarYouTube | ||
| date = 25 March 2015 | | date = 25 March 2015 | ||
| dates_alt_text = | | dates_alt_text = | ||
| vimeoID1 = | | vimeoID1 = 8sIC8WFyEQ0 | ||
| vimeoID2 = | | vimeoID2 = NHiTIGi5I5o | ||
| vimeoID3 = | | vimeoID3 = RGVepaP7AXk | ||
| vimeoID4 = | | vimeoID4 = VJC-0rPN7aY | ||
| vimeoID5 = | | vimeoID5 = IREdFiZXq2c | ||
| vimeoID6 = | | vimeoID6 = | ||
| vimeoID7 = | | vimeoID7 = | ||
| Line 19: | Line 19: | ||
| assignment_instructions = | | assignment_instructions = | ||
| assignment_solutions = | | assignment_solutions = | ||
| video_download_link_MP4 = | | video_download_link_MP4 = http://learnche.mcmaster.ca/media/2015-4G3-Class-11B.mp4 | ||
| video_download_link_MP4_size = 787 M | | video_download_link_MP4_size = 787 M | ||
| video_notes1 = | | video_notes1 = | ||
| video_download_link2_MP4 = | | video_download_link2_MP4 = http://learnche.mcmaster.ca/media/2015-4G3-Class-12A.mp4 | ||
| video_download_link2_MP4_size = 905 M | | video_download_link2_MP4_size = 905 M | ||
| video_notes2 = | | video_notes2 = | ||
| video_download_link3_MP4 = | | video_download_link3_MP4 = http://learnche.mcmaster.ca/media/2015-4G3-Class-12B.mp4 | ||
| video_download_link3_MP4_size = M | | video_download_link3_MP4_size = 884 M | ||
| video_notes3 = | | video_notes3 = | ||
| video_download_link4_MP4 = | | video_download_link4_MP4 = http://learnche.mcmaster.ca/media/2015-4G3-Class-13A.mp4 | ||
| video_download_link4_MP4_size = M | | video_download_link4_MP4_size = 952 M | ||
| video_notes4 = | | video_notes4 = | ||
| video_download_link5_MP4 = | | video_download_link5_MP4 = http://learnche.mcmaster.ca/media/2015-4G3-Class-13B.mp4 | ||
| video_download_link5_MP4_size = M | | video_download_link5_MP4_size = 994 M | ||
| video_notes5 = | | video_notes5 = | ||
}} | }} | ||
| Line 45: | Line 45: | ||
! Topic | ! Topic | ||
! Slides/handouts for class | ! Slides/handouts for class | ||
! References and Notes | ! References and Notes | ||
|- | |- | ||
| Line 55: | Line 54: | ||
| align="left" colspan="1"| | | align="left" colspan="1"| | ||
[https://docs.google.com/document/d/12jmwaBfvSu0l8Wn3KC0JIJGBqjdloteNQJMgkW6aQyY Handout from class] | [https://docs.google.com/document/d/12jmwaBfvSu0l8Wn3KC0JIJGBqjdloteNQJMgkW6aQyY Handout from class] | ||
|align="left" colspan="1"| | |align="left" colspan="1"| | ||
See the GAMS codes below | See the GAMS codes below | ||
| Line 69: | Line 67: | ||
| align="left" colspan="1"| | | align="left" colspan="1"| | ||
[https://docs.google.com/document/d/1EhXsp-Whc-DfgxvSkAAqu3jRyOcBo-HubWvOqpQ1LQg Handout from class] | [https://docs.google.com/document/d/1EhXsp-Whc-DfgxvSkAAqu3jRyOcBo-HubWvOqpQ1LQg Handout from class] | ||
|align="left" colspan="1"| | |align="left" colspan="1"| | ||
See the GAMS codes below | See the GAMS codes below | ||
| Line 79: | Line 76: | ||
| align="left" colspan="1"| | | align="left" colspan="1"| | ||
[https://docs.google.com/document/d/1MxIsIPG1uTNvAUFvyaHFUln1ClpUgTADi2HgbFPdkeU/edit?usp=sharing Handout from class] | [https://docs.google.com/document/d/1MxIsIPG1uTNvAUFvyaHFUln1ClpUgTADi2HgbFPdkeU/edit?usp=sharing Handout from class] | ||
[[Media:Sequence-of-branch-and-bound-steps-4G3-2015.pdf |Sequence of the branch and bound steps]] | |||
|align="left" colspan="1"| | |align="left" colspan="1"| | ||
See code below to solve the original problem, and then the relaxed problem | See code below to solve the original problem, and then the relaxed problem. | ||
See another example problem below (with solution). | |||
|- | |- | ||
| 06 April | | 06 April | ||
| 13A | | 13A | ||
| align="left" colspan="1"| | | align="left" colspan="1"| | ||
Working towards understanding schedule problems in engineering | |||
* | * Gantt chart approach | ||
* | * What the search variables mean | ||
* | * What objective function choices exist | ||
* | * Setting up the integer (disjunctive) variables constraints | ||
| align="left" colspan="1"| | | align="left" colspan="1"| | ||
[https://docs.google.com/document/d/1lmBL1Bh251VYb7NmBD2ER-JPD2DSExGR87nu7AWs7oo/ Handout from class] | |||
|align="left" colspan="1"| | |align="left" colspan="1"| | ||
See code below for the simple scheduling problem (3 products on 1 unit). | |||
|- | |||
| 08 April | |||
| 13B | |||
| align="left" colspan="1"| | |||
Scheduling problems | |||
Course wrap-up | |||
| align="left" colspan="1"| | |||
[https://docs.google.com/document/d/1VZRQ_aaQjMiK_brME9y1dhHYtkhTI_2NLt4PQ51OyhM Handout from class] | |||
|align="left" colspan="1"| | |||
* The first 10 pages of [http://www.inf.ufpr.br/aurora/disciplinas/topicosia2/livros/search/integer.pdf this textbook chapter] give some great background to integer programs, and how they are solved. | |||
* See code below for the multi-unit multi-product (3 products on 4 units) scheduling problem. | |||
|} | |} | ||
| Line 186: | Line 197: | ||
solve projects using mip maximizing value; | solve projects using mip maximizing value; | ||
</syntaxhighlight> | </syntaxhighlight> | ||
===Binary problem relaxation === | ===Binary problem relaxation === | ||
| Line 330: | Line 280: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
|} | |} | ||
=== Example problem to practice === | |||
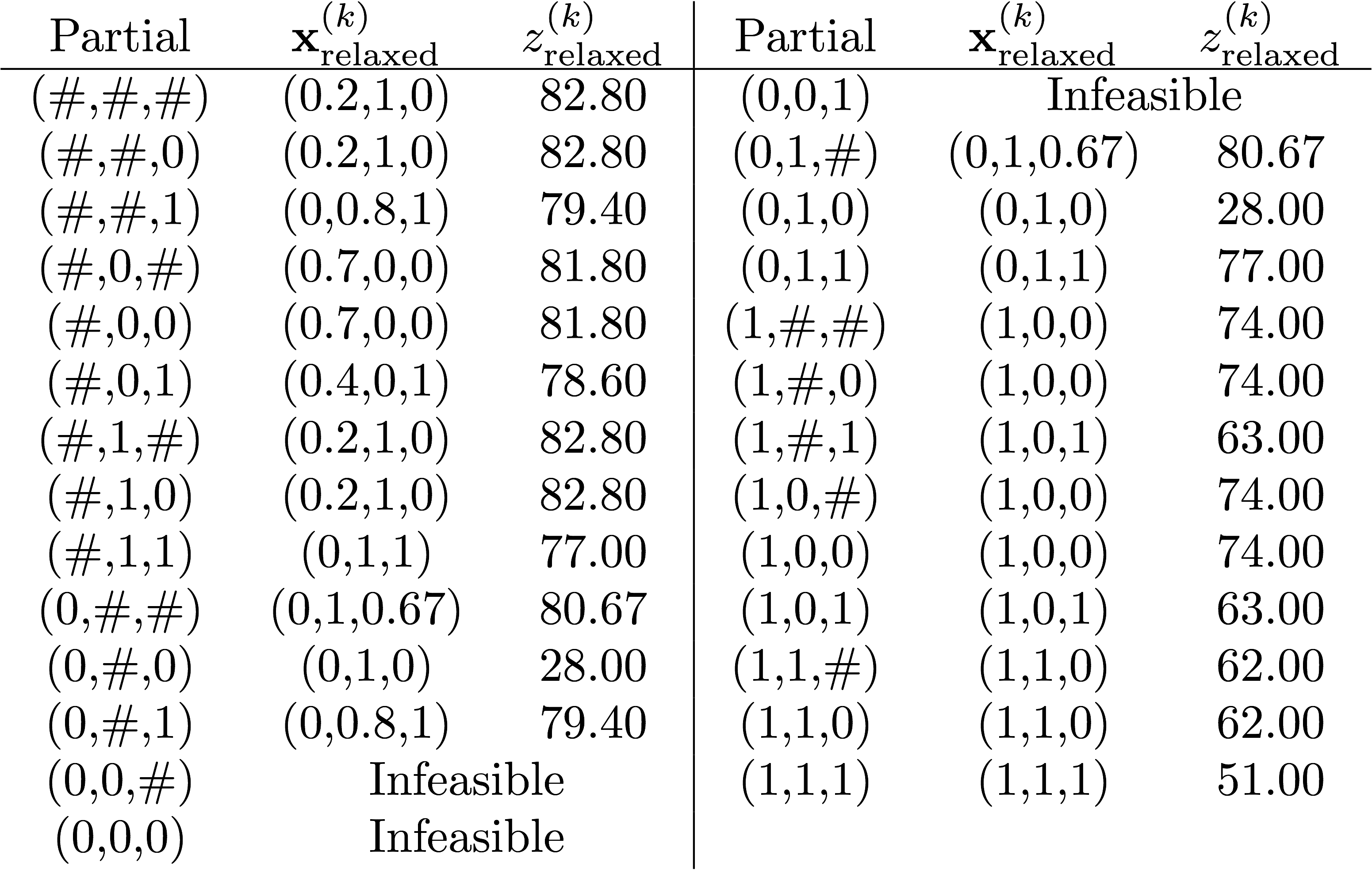
The objective is to '''''maximize''''' the objective function value, \(z\). The table or partial solutions is provided below. The only constraints are that all the 3 search variables must be binary (0 or 1). The "relaxed" refers to the relaxed problem solution. | |||
[[Image:4G3-2015-MIP-Practice-problem.png|750px]] | |||
Use the depth-first search method, and when branching, choose the branch with \(x_i = 0\) before the \(x_i=1\) branch. | |||
If you do this, your nodes will have the following solution order: | |||
Node 0 \((z=82.80)\) | |||
Node 1 \((z=80.67)\) | |||
Node 2 \((z=28.00)\) [incumbent] | |||
Node 3 \((z=79.4)\) | |||
Node 4 \((z=\text{Infeasible})\) | |||
Node 5 \((z=77.00)\) [incumbent; turns out this is the eventual optimum] | |||
Node 6 \((z=74.00)\) | |||
[The end: can you prove why?] | |||
<!-- | |||
\begin{center}\begin{tabular}{ccc|ccc} | |||
Partial & ${\bf x}_{\rm rel}^{(k)}$ & $z_{\rm rel}^{(k)}$ & Partial & ${\bf x}_{\rm rel}^{(k)}$ & $z_{\rm rel}^{(k)}$ \\ \hline | |||
(\#,\#,\#) & (0.2,1,0) & 82.80 & (0,0,1) & \multicolumn{2}{c}{Infeasible} \\ | |||
(\#,\#,0) & (0.2,1,0) & 82.80 & (0,1,\#) & (0,1,0.67) & 80.67 \\ | |||
(\#,\#,1) & (0,0.8,1) & 79.40 & (0,1,0) & (0,1,0) & 28.00 \\ | |||
(\#,0,\#) & (0.7,0,0) & 81.80 & (0,1,1) & (0,1,1) & 77.00 \\ | |||
(\#,0,0) & (0.7,0,0) & 81.80 & (1,\#,\#) & (1,0,0) & 74.00 \\ | |||
(\#,0,1) & (0.4,0,1) & 78.60 & (1,\#,0) & (1,0,0) & 74.00 \\ | |||
(\#,1,\#) & (0.2,1,0) & 82.80 & (1,\#,1) & (1,0,1) & 63.00 \\ | |||
(\#,1,0) & (0.2,1,0) & 82.80 & (1,0,\#) & (1,0,0) & 74.00 \\ | |||
(\#,1,1) & (0,1,1) & 77.00 & (1,0,0) & (1,0,0) & 74.00 \\ | |||
(0,\#,\#) & (0,1,0.67) & 80.67 & (1,0,1) & (1,0,1) & 63.00 \\ | |||
(0,\#,0) & (0,1,0) & 28.00 & (1,1,\#) & (1,1,0) & 62.00 \\ | |||
(0,\#,1) & (0,0.8,1) & 79.40 & (1,1,0) & (1,1,0) & 62.00 \\ | |||
(0,0,\#) & \multicolumn{2}{c|}{Infeasible} & (1,1,1) & (1,1,1) & 51.00 \\ | |||
(0,0,0) & \multicolumn{2}{c|}{Infeasible} & \\ | |||
\end{tabular}\end{center} | |||
--> | |||
=== Simple schedule: one unit, 3 products === | |||
This example was covered in [https://docs.google.com/document/d/1lmBL1Bh251VYb7NmBD2ER-JPD2DSExGR87nu7AWs7oo class 13A]: | |||
<syntaxhighlight lang="python"> | |||
set j "jobs" /1*3/; | |||
alias (j,jp); | |||
parameter p(j) "process time of j" | |||
/ 1 15, 2 6, 3 9/; | |||
scalar M "bigM"; | |||
M = sum(j, p(j)); | |||
free variable MeanComp "Mean completion time"; | |||
positive variables x(j) "Start time of job j"; | |||
binary variables y(j,jp) "Disjunctive variable for j and jp"; | |||
EQUATIONS | |||
MeanCeqn "Mean completion time", | |||
Disj1(j,jp) "Disjunctive part 1", | |||
Disj2(j,jp) "Disjunctive part 2"; | |||
MeanCeqn.. MeanComp =E= sum(j, x(j)+p(j) ) / card(j); | |||
Disj1(j,jp)$(ord(j) lt ord(jp)).. x(j) + p(j) =L= x(jp) + M*(1-y(j,jp)); | |||
Disj2(j,jp)$(ord(j) lt ord(jp)).. x(jp)+ p(jp) =L= x(j) + M*y(j,jp); | |||
MODEL simplesched /all/; | |||
SOLVE simplesched using MIP minimizing MeanComp; | |||
</syntaxhighlight> | |||
=== Scheduling 3 products on 4 units === | |||
This example was covered in [https://docs.google.com/document/d/1VZRQ_aaQjMiK_brME9y1dhHYtkhTI_2NLt4PQ51OyhM/edit class 13B]: | |||
<syntaxhighlight lang="python"> | |||
* Based on: https://comp.uark.edu/~rrardin/oorbook/software/gams/custommw.gms | |||
set j "Products" /A*C/, | |||
k "Units" /1*4/; | |||
alias (j,jp); | |||
alias (k,kp); | |||
set succ(j,k,kp) "Product j successor pairs" | |||
/A.1.2, A.2.3, A.3.4, | |||
B.3.4, | |||
C.3.2, C.2.4/; | |||
TABLE p(j,k) "Process time of product j on unit k" | |||
1 2 3 4 | |||
A 1 5 4.0 1.5 | |||
B 0 0 4.5 1.0 | |||
C 0 3 5.0 1.5; | |||
scalar M "bigM"; | |||
M = sum((j,k), p(j,k)); | |||
FREE variable | |||
AverageC "Average completion time"; | |||
POSITIVE variables x(j,k) "Start time of job (product) j on unit k: j.k"; | |||
BINARY variables y(j,jp,k) "Disjunctive variable for j and jp on k"; | |||
EQUATIONS | |||
avgComplete "Average completeness", | |||
pred(j,k,kp) "Precedence within jobs", | |||
disj1(j,jp,k) "Disjunctive part 1 for j and jp on k", | |||
disj2(j,jp,k) "Disjunctive part 2 for j and jp on k"; | |||
avgComplete.. AverageC =E= sum((j,k), x(j,k)+p(j,k) ); | |||
* These are the precedence constraints | |||
pred(j,k,kp)$succ(j,k,kp).. x(j,k) + p(j,k) =L= x(j,kp); | |||
disj1(j,jp,k)$(ord(j) lt ord(jp) and p(j,k) gt 0 and p(jp,k) gt 0).. | |||
x(j,k) + p(j,k) =L= x(jp,k) + M*(1-y(j,jp,k)); | |||
disj2(j,jp,k)$(ord(j) lt ord(jp) and p(j,k) gt 0 and p(jp,k) gt 0).. | |||
x(jp,k) + p(jp,k) =L= x(j,k) + M*y(j,jp,k); | |||
MODEL Jobshop /all/; | |||
option mip = mosek; | |||
SOLVE Jobshop USING MIP minimizing AverageC; | |||
</syntaxhighlight> | |||
Latest revision as of 11:55, 12 August 2018
| Class date(s): | 25 March 2015 | ||||
|
| |||||
|
| |||||
|
| |||||
|
| |||||
|
| |||||
Resources
Scroll down, if necessary, to see the resources.
| Date | Class number | Topic | Slides/handouts for class | References and Notes |
|---|---|---|---|---|
| 25 March | 11B |
|
See the GAMS codes below | |
| 30 March | 12A |
More problems that can be solved with integer variables
|
See the GAMS codes below | |
| 01 April | 12B |
The branch and bound procedure to solve integer problems |
See code below to solve the original problem, and then the relaxed problem. See another example problem below (with solution). | |
| 06 April | 13A |
Working towards understanding schedule problems in engineering
|
See code below for the simple scheduling problem (3 products on 1 unit). | |
| 08 April | 13B |
Scheduling problems Course wrap-up |
|
Solving a basic ILP
free variable income "total income";
positive variables x1, x2;
binary variable delta "use ingredient x3 or not at all";
EQUATIONS
obj "maximize income",
blend "blending constraint";
obj.. income =E= 18*x1 - 3*x2 - 9*(20*delta);
blend.. 2*x1 + x2 + 7*(20*delta) =L= 150;
x1.up = 25;
x2.up = 30;
model recipe /all/;
SOLVE recipe using MIP maximizing income;
Solving the knapsack problem
free variable value "total value";
sets j "item j" /1*5/;
binary variables x(j) "whether to include item in the knapsack";
parameter v(j) "value of object j"
/1 4,
2 2,
3 10,
4 1,
5 2/;
parameter w(j) "weight of object j"
/1 12,
2 1,
3 4,
4 1,
5 2/;
EQUATIONS
obj "maximize value",
weight "weight constraint";
obj.. value =e= sum(j, v(j)*x(j));
weight.. sum(j, w(j)*x(j)) =L= 15;
model knapsack /all/;
solve knapsack using mip maximizing value;
Solving the knapsack problem for selecting amount projects, with constraints
free variable value "total value";
sets j "item j" /1*5/;
binary variables x(j) "whether to include item in the project";
parameter v(j) "value of object j"
/1 50,
2 72,
3 25,
4 41,
5 17/;
parameter w(j) "cost of object j"
/1 8,
2 21,
3 15,
4 10,
5 7/;
EQUATIONS
obj "maximize value",
weight "weight constraint",
me1v2 "1 and 2 are mutually exclusive",
me1v3v5 "1, 3 and 5 are mutually exclusive",
d4v3 "4 depends on 3";
obj.. value =e= sum(j, v(j)*x(j));
weight.. sum(j, w(j)*x(j)) =L= 35;
me1v2.. x('1') + x('2') =L= 1;
me1v3v5.. x('1') + x('3') + x('5') =L= 1;
d4v3.. x('4') =L= x('3');
model projects /all/;
solve projects using mip maximizing value;
Binary problem relaxation
This is the problem we looked at in class for the generators.
Notice that the only differences are:
- the binary variables become positive variables, thepr
- the problem is solved as an LP not an MIP
- the constraints for .LO and .UP are added, where required, depending on the partial solution solved
| Original problem solved in class | Relaxed problem solved in class |
|---|---|
free variable cost "total cost";
sets j "item j" /1*4/;
binary variables x(j) "whether to use generator";
parameter c(j) "cost of using generator j"
/1 7,
2 12,
3 5,
4 14/;
parameter p(j) "power of generator j"
/1 300,
2 600,
3 500,
4 1600/;
EQUATIONS
obj "cost",
power_constraint;
obj.. cost =e= sum(j, c(j)*x(j));
power_constraint.. sum(j, p(j)*x(j)) =G= 700;
MODEL purchase /all/;
SOLVE purchase using MIP minimizing cost;
|
free variable cost "total cost";
sets j "item j" /1*4/;
positive variables x(j) "whether to use generator";
parameter c(j) "cost of using generator j"
/1 7,
2 12,
3 5,
4 14/;
parameter p(j) "power of generator j"
/1 300,
2 600,
3 500,
4 1600/;
EQUATIONS
obj "cost",
power_constraint;
obj.. cost =e= sum(j, c(j)*x(j));
power_constraint.. sum(j, p(j)*x(j)) =G= 700;
* Solve the problem for the partial solution: (#, 0, #, 1)
x.LO('1')=0;
x.UP('1')=1;
x.LO('2')=0;
x.UP('2')=0;
x.LO('3')=0;
x.UP('3')=1;
x.LO('4')=1;
x.UP('4')=1;
MODEL purchase /all/;
SOLVE purchase using LP minimizing cost;
|
Example problem to practice
The objective is to maximize the objective function value, \(z\). The table or partial solutions is provided below. The only constraints are that all the 3 search variables must be binary (0 or 1). The "relaxed" refers to the relaxed problem solution.
Use the depth-first search method, and when branching, choose the branch with \(x_i = 0\) before the \(x_i=1\) branch.
If you do this, your nodes will have the following solution order:
Node 0 \((z=82.80)\)
Node 1 \((z=80.67)\)
Node 2 \((z=28.00)\) [incumbent]
Node 3 \((z=79.4)\)
Node 4 \((z=\text{Infeasible})\)
Node 5 \((z=77.00)\) [incumbent; turns out this is the eventual optimum]
Node 6 \((z=74.00)\)
[The end: can you prove why?]
Simple schedule: one unit, 3 products
This example was covered in class 13A:
set j "jobs" /1*3/;
alias (j,jp);
parameter p(j) "process time of j"
/ 1 15, 2 6, 3 9/;
scalar M "bigM";
M = sum(j, p(j));
free variable MeanComp "Mean completion time";
positive variables x(j) "Start time of job j";
binary variables y(j,jp) "Disjunctive variable for j and jp";
EQUATIONS
MeanCeqn "Mean completion time",
Disj1(j,jp) "Disjunctive part 1",
Disj2(j,jp) "Disjunctive part 2";
MeanCeqn.. MeanComp =E= sum(j, x(j)+p(j) ) / card(j);
Disj1(j,jp)$(ord(j) lt ord(jp)).. x(j) + p(j) =L= x(jp) + M*(1-y(j,jp));
Disj2(j,jp)$(ord(j) lt ord(jp)).. x(jp)+ p(jp) =L= x(j) + M*y(j,jp);
MODEL simplesched /all/;
SOLVE simplesched using MIP minimizing MeanComp;
Scheduling 3 products on 4 units
This example was covered in class 13B:
* Based on: https://comp.uark.edu/~rrardin/oorbook/software/gams/custommw.gms
set j "Products" /A*C/,
k "Units" /1*4/;
alias (j,jp);
alias (k,kp);
set succ(j,k,kp) "Product j successor pairs"
/A.1.2, A.2.3, A.3.4,
B.3.4,
C.3.2, C.2.4/;
TABLE p(j,k) "Process time of product j on unit k"
1 2 3 4
A 1 5 4.0 1.5
B 0 0 4.5 1.0
C 0 3 5.0 1.5;
scalar M "bigM";
M = sum((j,k), p(j,k));
FREE variable
AverageC "Average completion time";
POSITIVE variables x(j,k) "Start time of job (product) j on unit k: j.k";
BINARY variables y(j,jp,k) "Disjunctive variable for j and jp on k";
EQUATIONS
avgComplete "Average completeness",
pred(j,k,kp) "Precedence within jobs",
disj1(j,jp,k) "Disjunctive part 1 for j and jp on k",
disj2(j,jp,k) "Disjunctive part 2 for j and jp on k";
avgComplete.. AverageC =E= sum((j,k), x(j,k)+p(j,k) );
* These are the precedence constraints
pred(j,k,kp)$succ(j,k,kp).. x(j,k) + p(j,k) =L= x(j,kp);
disj1(j,jp,k)$(ord(j) lt ord(jp) and p(j,k) gt 0 and p(jp,k) gt 0)..
x(j,k) + p(j,k) =L= x(jp,k) + M*(1-y(j,jp,k));
disj2(j,jp,k)$(ord(j) lt ord(jp) and p(j,k) gt 0 and p(jp,k) gt 0)..
x(jp,k) + p(jp,k) =L= x(j,k) + M*y(j,jp,k);
MODEL Jobshop /all/;
option mip = mosek;
SOLVE Jobshop USING MIP minimizing AverageC;