Difference between revisions of "Mixed-Integer linear programming"
Kevin Dunn (talk | contribs) |
Kevin Dunn (talk | contribs) |
||
| Line 19: | Line 19: | ||
| assignment_instructions = | | assignment_instructions = | ||
| assignment_solutions = | | assignment_solutions = | ||
| video_download_link_MP4 = https:// | | video_download_link_MP4 = https://drive.google.com/open?id=0B9qiArsxgE8YdTNCM3E1U19UQU0&authuser=0 | ||
| video_download_link_MP4_size = 787 M | | video_download_link_MP4_size = 787 M | ||
| video_notes1 = | | video_notes1 = | ||
| video_download_link2_MP4 = https:// | | video_download_link2_MP4 = https://drive.google.com/open?id=0B9qiArsxgE8YM0o1NW52X2dPblE&authuser=0 | ||
| video_download_link2_MP4_size = 905 M | | video_download_link2_MP4_size = 905 M | ||
| video_notes2 = | | video_notes2 = | ||
| video_download_link3_MP4 = https:// | | video_download_link3_MP4 = https://drive.google.com/open?id=0B9qiArsxgE8YRmNxbG11M2R3amc&authuser=0 | ||
| video_download_link3_MP4_size = 884 M | | video_download_link3_MP4_size = 884 M | ||
| video_notes3 = | | video_notes3 = | ||
| video_download_link4_MP4 = https:// | | video_download_link4_MP4 = https://drive.google.com/open?id=0B9qiArsxgE8YQXBtVlhvaUJDY3M&authuser=0 | ||
| video_download_link4_MP4_size = 952 M | | video_download_link4_MP4_size = 952 M | ||
| video_notes4 = | | video_notes4 = | ||
| video_download_link5_MP4 = https:// | | video_download_link5_MP4 = https://drive.google.com/open?id=0B9qiArsxgE8YTE9QaFdOTmw3bVU&authuser=0 | ||
| video_download_link5_MP4_size = 994 M | | video_download_link5_MP4_size = 994 M | ||
| video_notes5 = | | video_notes5 = | ||
| Line 55: | Line 55: | ||
| align="left" colspan="1"| | | align="left" colspan="1"| | ||
[https://docs.google.com/document/d/12jmwaBfvSu0l8Wn3KC0JIJGBqjdloteNQJMgkW6aQyY Handout from class] | [https://docs.google.com/document/d/12jmwaBfvSu0l8Wn3KC0JIJGBqjdloteNQJMgkW6aQyY Handout from class] | ||
| [https:// | | [https://drive.google.com/open?id=0B9qiArsxgE8YdTNCM3E1U19UQU0&authuser=0 Video] | ||
|align="left" colspan="1"| | |align="left" colspan="1"| | ||
See the GAMS codes below | See the GAMS codes below | ||
| Line 69: | Line 69: | ||
| align="left" colspan="1"| | | align="left" colspan="1"| | ||
[https://docs.google.com/document/d/1EhXsp-Whc-DfgxvSkAAqu3jRyOcBo-HubWvOqpQ1LQg Handout from class] | [https://docs.google.com/document/d/1EhXsp-Whc-DfgxvSkAAqu3jRyOcBo-HubWvOqpQ1LQg Handout from class] | ||
| [https:// | | [https://drive.google.com/open?id=0B9qiArsxgE8YM0o1NW52X2dPblE&authuser=0 Video] | ||
|align="left" colspan="1"| | |align="left" colspan="1"| | ||
See the GAMS codes below | See the GAMS codes below | ||
| Line 81: | Line 81: | ||
[[Media:Sequence-of-branch-and-bound-steps-4G3-2015.pdf |Sequence of the branch and bound steps]] | [[Media:Sequence-of-branch-and-bound-steps-4G3-2015.pdf |Sequence of the branch and bound steps]] | ||
| [https:// | | [https://drive.google.com/open?id=0B9qiArsxgE8YRmNxbG11M2R3amc&authuser=0 Video] | ||
|align="left" colspan="1"| | |align="left" colspan="1"| | ||
See code below to solve the original problem, and then the relaxed problem. | See code below to solve the original problem, and then the relaxed problem. | ||
| Line 97: | Line 97: | ||
| align="left" colspan="1"| | | align="left" colspan="1"| | ||
[https://docs.google.com/document/d/1lmBL1Bh251VYb7NmBD2ER-JPD2DSExGR87nu7AWs7oo/ Handout from class] | [https://docs.google.com/document/d/1lmBL1Bh251VYb7NmBD2ER-JPD2DSExGR87nu7AWs7oo/ Handout from class] | ||
| [https:// | | [https://drive.google.com/open?id=0B9qiArsxgE8YQXBtVlhvaUJDY3M&authuser=0 Video] | ||
|align="left" colspan="1"| | |align="left" colspan="1"| | ||
See code below for the simple scheduling problem (3 products on 1 unit). | See code below for the simple scheduling problem (3 products on 1 unit). | ||
| Line 109: | Line 109: | ||
| align="left" colspan="1"| | | align="left" colspan="1"| | ||
[https://docs.google.com/document/d/1VZRQ_aaQjMiK_brME9y1dhHYtkhTI_2NLt4PQ51OyhM Handout from class] | [https://docs.google.com/document/d/1VZRQ_aaQjMiK_brME9y1dhHYtkhTI_2NLt4PQ51OyhM Handout from class] | ||
| [https:// | | [https://drive.google.com/open?id=0B9qiArsxgE8YTE9QaFdOTmw3bVU&authuser=0 Video] | ||
|align="left" colspan="1"| | |align="left" colspan="1"| | ||
* The first 10 pages of [http://www.inf.ufpr.br/aurora/disciplinas/topicosia2/livros/search/integer.pdf this textbook chapter] give some great background to integer programs, and how they are solved. | * The first 10 pages of [http://www.inf.ufpr.br/aurora/disciplinas/topicosia2/livros/search/integer.pdf this textbook chapter] give some great background to integer programs, and how they are solved. | ||
Revision as of 14:20, 13 April 2015
| Class date(s): | 25 March 2015 | ||||
| |||||
| |||||
| |||||
| |||||
| |||||
Resources
Scroll down, if necessary, to see the resources.
| Date | Class number | Topic | Slides/handouts for class | Video file | References and Notes |
|---|---|---|---|---|---|
| 25 March | 11B |
|
Video |
See the GAMS codes below | |
| 30 March | 12A |
More problems that can be solved with integer variables
|
Video |
See the GAMS codes below | |
| 01 April | 12B |
The branch and bound procedure to solve integer problems |
Video |
See code below to solve the original problem, and then the relaxed problem. See another example problem below (with solution). | |
| 06 April | 13A |
Working towards understanding schedule problems in engineering
|
Video |
See code below for the simple scheduling problem (3 products on 1 unit). | |
| 08 April | 13B |
Scheduling problems Course wrap-up |
Video |
|
Solving a basic ILP
free variable income "total income";
positive variables x1, x2;
binary variable delta "use ingredient x3 or not at all";
EQUATIONS
obj "maximize income",
blend "blending constraint";
obj.. income =E= 18*x1 - 3*x2 - 9*(20*delta);
blend.. 2*x1 + x2 + 7*(20*delta) =L= 150;
x1.up = 25;
x2.up = 30;
model recipe /all/;
SOLVE recipe using MIP maximizing income;
Solving the knapsack problem
free variable value "total value";
sets j "item j" /1*5/;
binary variables x(j) "whether to include item in the knapsack";
parameter v(j) "value of object j"
/1 4,
2 2,
3 10,
4 1,
5 2/;
parameter w(j) "weight of object j"
/1 12,
2 1,
3 4,
4 1,
5 2/;
EQUATIONS
obj "maximize value",
weight "weight constraint";
obj.. value =e= sum(j, v(j)*x(j));
weight.. sum(j, w(j)*x(j)) =L= 15;
model knapsack /all/;
solve knapsack using mip maximizing value;
Solving the knapsack problem for selecting amount projects, with constraints
free variable value "total value";
sets j "item j" /1*5/;
binary variables x(j) "whether to include item in the project";
parameter v(j) "value of object j"
/1 50,
2 72,
3 25,
4 41,
5 17/;
parameter w(j) "cost of object j"
/1 8,
2 21,
3 15,
4 10,
5 7/;
EQUATIONS
obj "maximize value",
weight "weight constraint",
me1v2 "1 and 2 are mutually exclusive",
me1v3v5 "1, 3 and 5 are mutually exclusive",
d4v3 "4 depends on 3";
obj.. value =e= sum(j, v(j)*x(j));
weight.. sum(j, w(j)*x(j)) =L= 35;
me1v2.. x('1') + x('2') =L= 1;
me1v3v5.. x('1') + x('3') + x('5') =L= 1;
d4v3.. x('4') =L= x('3');
model projects /all/;
solve projects using mip maximizing value;
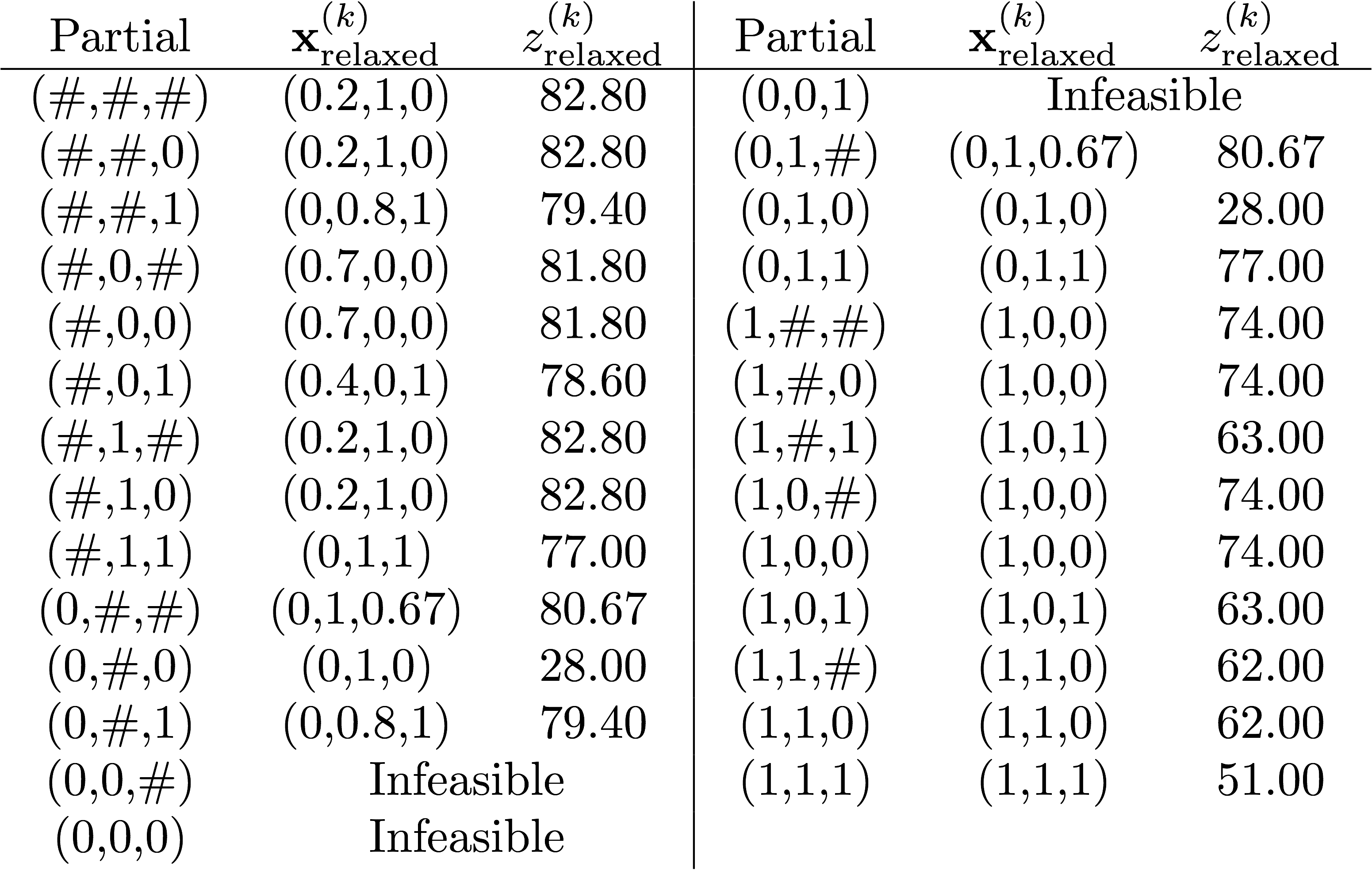
Binary problem relaxation
This is the problem we looked at in class for the generators.
Notice that the only differences are:
- the binary variables become positive variables, thepr
- the problem is solved as an LP not an MIP
- the constraints for .LO and .UP are added, where required, depending on the partial solution solved
| Original problem solved in class | Relaxed problem solved in class |
|---|---|
free variable cost "total cost";
sets j "item j" /1*4/;
binary variables x(j) "whether to use generator";
parameter c(j) "cost of using generator j"
/1 7,
2 12,
3 5,
4 14/;
parameter p(j) "power of generator j"
/1 300,
2 600,
3 500,
4 1600/;
EQUATIONS
obj "cost",
power_constraint;
obj.. cost =e= sum(j, c(j)*x(j));
power_constraint.. sum(j, p(j)*x(j)) =G= 700;
MODEL purchase /all/;
SOLVE purchase using MIP minimizing cost;
|
free variable cost "total cost";
sets j "item j" /1*4/;
positive variables x(j) "whether to use generator";
parameter c(j) "cost of using generator j"
/1 7,
2 12,
3 5,
4 14/;
parameter p(j) "power of generator j"
/1 300,
2 600,
3 500,
4 1600/;
EQUATIONS
obj "cost",
power_constraint;
obj.. cost =e= sum(j, c(j)*x(j));
power_constraint.. sum(j, p(j)*x(j)) =G= 700;
* Solve the problem for the partial solution: (#, 0, #, 1)
x.LO('1')=0;
x.UP('1')=1;
x.LO('2')=0;
x.UP('2')=0;
x.LO('3')=0;
x.UP('3')=1;
x.LO('4')=1;
x.UP('4')=1;
MODEL purchase /all/;
SOLVE purchase using LP minimizing cost;
|
Example problem to practice
The objective is to maximize the objective function value,
Use the depth-first search method, and when branching, choose the branch with
If you do this, your nodes will have the following solution order:
Node 0
Node 1
Node 2
Node 3
Node 4
Node 5
Node 6
[The end: can you prove why?]
Simple schedule: one unit, 3 products
This example was covered in class 13A:
set j "jobs" /1*3/;
alias (j,jp);
parameter p(j) "process time of j"
/ 1 15, 2 6, 3 9/;
scalar M "bigM";
M = sum(j, p(j));
free variable MeanComp "Mean completion time";
positive variables x(j) "Start time of job j";
binary variables y(j,jp) "Disjunctive variable for j and jp";
EQUATIONS
MeanCeqn "Mean completion time",
Disj1(j,jp) "Disjunctive part 1",
Disj2(j,jp) "Disjunctive part 2";
MeanCeqn.. MeanComp =E= sum(j, x(j)+p(j) ) / card(j);
Disj1(j,jp)$(ord(j) lt ord(jp)).. x(j) + p(j) =L= x(jp) + M*(1-y(j,jp));
Disj2(j,jp)$(ord(j) lt ord(jp)).. x(jp)+ p(jp) =L= x(j) + M*y(j,jp);
MODEL simplesched /all/;
SOLVE simplesched using MIP minimizing MeanComp;
Scheduling 3 products on 4 units
This example was covered in class 13B:
* Based on: https://comp.uark.edu/~rrardin/oorbook/software/gams/custommw.gms
set j "Products" /A*C/,
k "Units" /1*4/;
alias (j,jp);
alias (k,kp);
set succ(j,k,kp) "Product j successor pairs"
/A.1.2, A.2.3, A.3.4,
B.3.4,
C.3.2, C.2.4/;
TABLE p(j,k) "Process time of product j on unit k"
1 2 3 4
A 1 5 4.0 1.5
B 0 0 4.5 1.0
C 0 3 5.0 1.5;
scalar M "bigM";
M = sum((j,k), p(j,k));
FREE variable
AverageC "Average completion time";
POSITIVE variables x(j,k) "Start time of job (product) j on unit k: j.k";
BINARY variables y(j,jp,k) "Disjunctive variable for j and jp on k";
EQUATIONS
avgComplete "Average completeness",
pred(j,k,kp) "Precedence within jobs",
disj1(j,jp,k) "Disjunctive part 1 for j and jp on k",
disj2(j,jp,k) "Disjunctive part 2 for j and jp on k";
avgComplete.. AverageC =E= sum((j,k), x(j,k)+p(j,k) );
* These are the precedence constraints
pred(j,k,kp)$succ(j,k,kp).. x(j,k) + p(j,k) =L= x(j,kp);
disj1(j,jp,k)$(ord(j) lt ord(jp) and p(j,k) gt 0 and p(jp,k) gt 0)..
x(j,k) + p(j,k) =L= x(jp,k) + M*(1-y(j,jp,k));
disj2(j,jp,k)$(ord(j) lt ord(jp) and p(j,k) gt 0 and p(jp,k) gt 0)..
x(jp,k) + p(jp,k) =L= x(j,k) + M*y(j,jp,k);
MODEL Jobshop /all/;
option mip = mosek;
SOLVE Jobshop USING MIP minimizing AverageC;