Software tutorial/Least squares modelling (linear regression)
One of the best packages for fitting least squares models, in addition to all sorts of other statistical manipulation of data is the R language. The following pages from the 4C3 (Statistics for Engineering) website will help you:
However, here is a tutorial on how you can use MATLAB or Python to fit a least squares model.
- MATLAB: use the regress.m and regstats.m functions - if you have the Statistics Toolbox, otherwise use the code below
- Python: use the numpy.linalg.lstsq function
Single-variable regression
| MATLAB | Python |
|---|---|
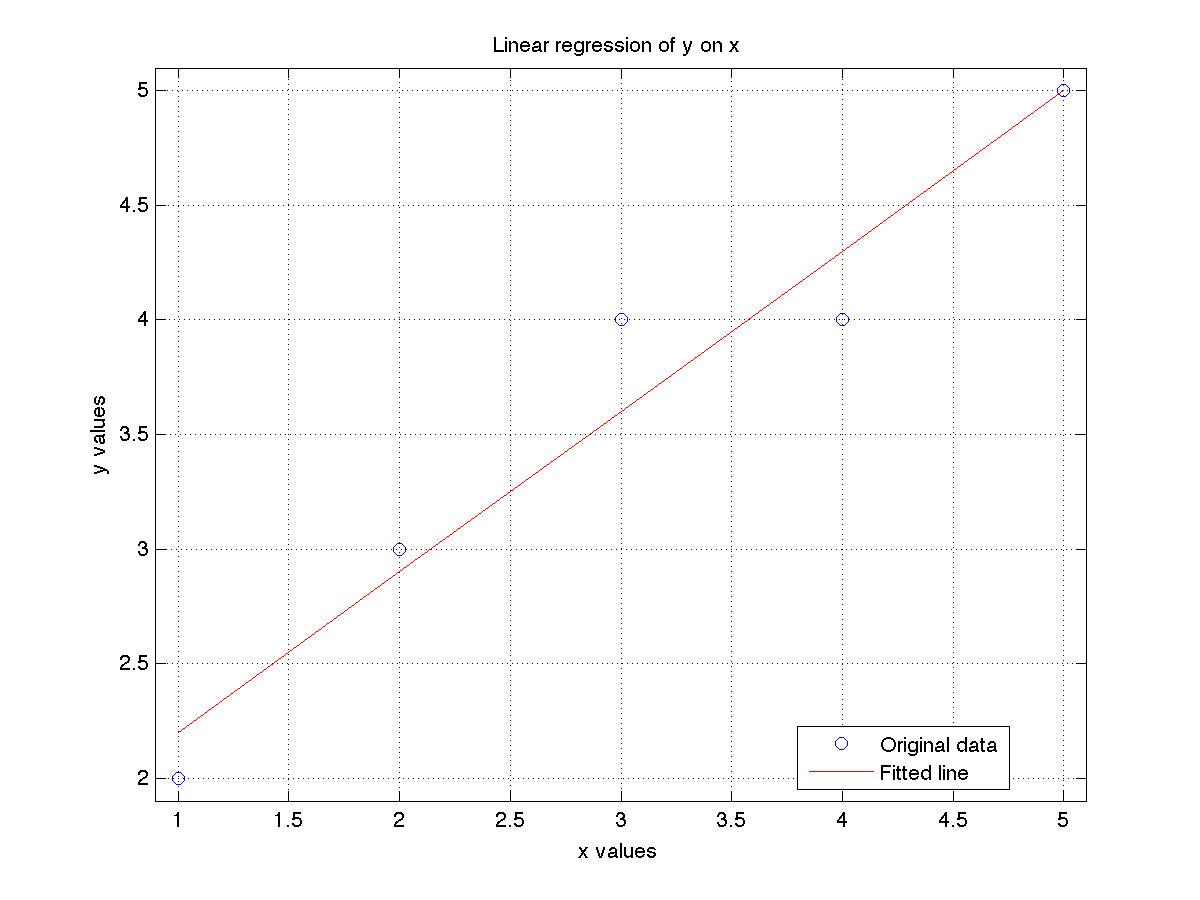
x = [1, 2, 3, 4, 5];
y = [2, 3, 4, 4, 5];
y = y(:);
n = numel(x); % the number of observations
X = [ones(n,1) x(:)];
a = inv(X'*X)*X'*y; % Contains a_0=a(1) and a_1=a(2)
a = regress(y, X); % only if you have the Statistics Toolbox
% Plot the data along with the fitted line:
plot(x, y, 'o')
hold('on')
grid('on')
plot(x, X*a, 'r')
xlabel('x values')
ylabel('y values')
title('Linear regression of y on x')
xlim([0.9, 5.1])
ylim([1.9, 5.1])
legend({'Original data', 'Fitted line'}, 'Location', 'Best')
% Additional calculations
resids = y - X*a; % resids = e = y - Xa
RSS = resids' * resids; % residual sum of squares
TSS = sum((y - mean(y)).^2); % total sum of squares
R2 = 1 - RSS/TSS;
std_error = sqrt(RSS/(n-numel(a)));
std_y = sqrt(TSS/(n-1)); % just the same as std(y)
R2_adj = 1 - (std_error/std_y)^2;
|
import numpy as np
from matplotlib.pyplot import *
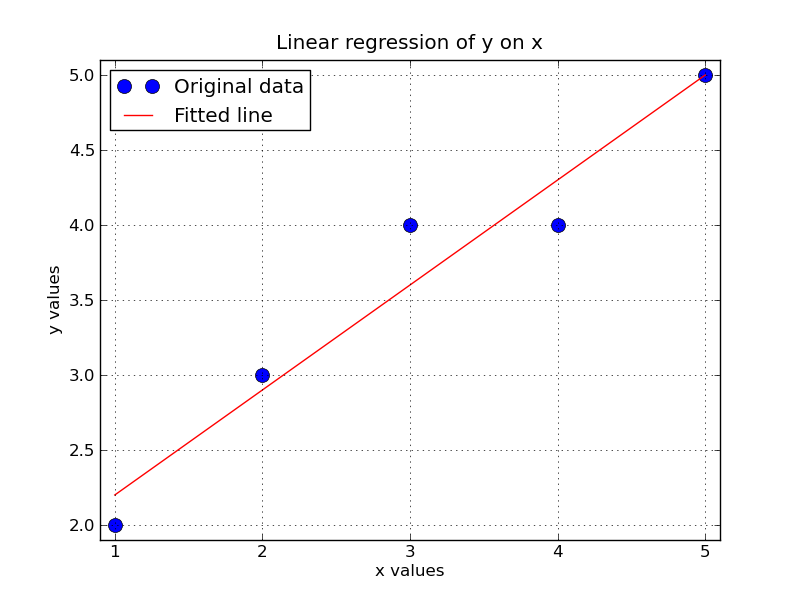
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 4, 4, 5])
n = np.max(x.shape) # the number of observations
X = np.vstack([np.ones(n), x]).T
# More complex, and less accurate in some cases:
y = y.reshape((n,1))
XTX_inv = np.linalg.inv(np.dot(X.T, X))
a = np.dot(np.dot(XTX_inv, X.T), y)
# Simpler, and more accurate way:
a = np.linalg.lstsq(X, y)[0]
# Plot the data along with the fitted line:
plot(x, y, 'o', label='Original data', markersize=10)
plot(x, np.dot(X,a), 'r', label='Fitted line')
xlabel('x values')
ylabel('y values')
title('Linear regression of y on x')
grid('on')
xlim([0.9, 5.1])
ylim([1.9, 5.1])
legend(loc=0)
# Additional calculations
resids = y - np.dot(X,a) # e = y - Xa;
RSS = sum(resids**2) # residual sum of squares
TSS = sum((y - np.mean(y))**2) # total sum of squares
R2 = 1 - RSS/TSS
std_error = np.sqrt(RSS/(n-len(a)))
std_y = np.sqrt(TSS/(n-1))
R2_adj = 1 - (std_error/std_y)**2
|
Matlab provides the function regstats that can be used as follows:
>> regstats(y, x)
to show additional regression statistics. However, all the outputs from a linear model that we require for this course are computed in the code shown above. Python does not have a similar function (to my knowledge).
Regression when the intercept is zero
The above code can also be used in the case when \(a_0\) is known to be zero in the least squares model: \( y=a_0 + a_1 x\). Simply adjust the X matrix in the above code to be a single column by omitting the column of ones.
Multiple linear regression
The case for multiple linear regression is identical to that shown above. The only difference is that you have to expand the X matrix with extra columns. The least squares coefficients in vector a are returned in the same order as the columns in matrix X.
Your coefficients from the linear model can also be calculated from: \[\bf a = \left(X^{T}X\right)^{-1} X^{T}y \] though the MATLAB and Python functions will not compute them this way (they use either a QR or SV decomposition algorithm).