Difference between revisions of "Software tutorial/Least squares modelling (linear regression)"
Jump to navigation
Jump to search
m |
m |
||
| Line 8: | Line 8: | ||
* MATLAB: use the <tt>regress.m</tt> and <tt>regstats.m</tt> function | * MATLAB: use the <tt>regress.m</tt> and <tt>regstats.m</tt> function | ||
* Python: use the [http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.lstsq.html <tt>numpy.linalg.lstsq</tt>] function | * Python: use the [http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.lstsq.html <tt>numpy.linalg.lstsq</tt>] function | ||
{| class="wikitable" | {| class="wikitable" | ||
| Line 47: | Line 46: | ||
R2_adj = 1 - (std_error/std_y)^2 | R2_adj = 1 - (std_error/std_y)^2 | ||
</syntaxhighlight> | </syntaxhighlight> | ||
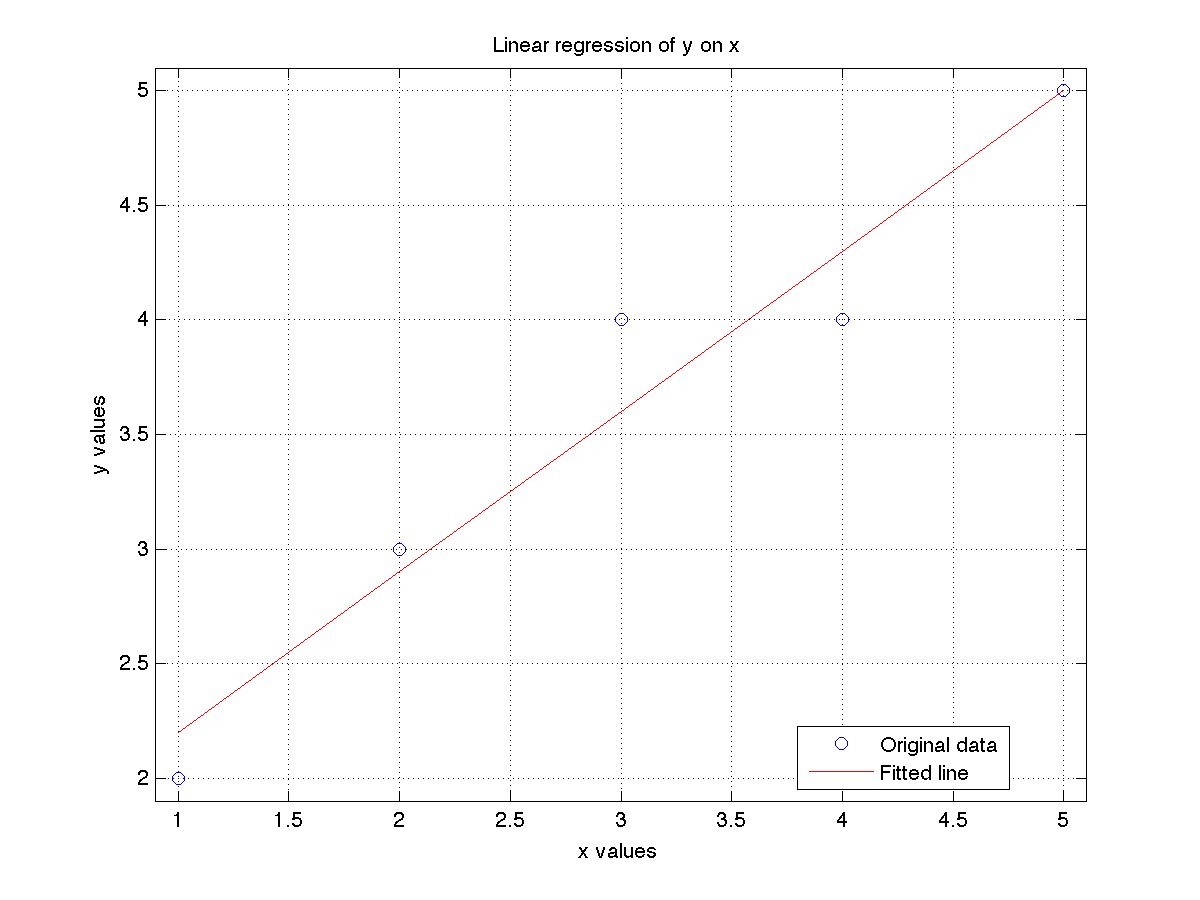
[[Image:Least-squares-MATLAB.png | 550px]] | |||
| width="50%" valign="top" | | | width="50%" valign="top" | | ||
<syntaxhighlight lang="python"> | |||
import numpy as np | |||
from matplotlib.pyplot import * | |||
x = np.array([1, 2, 3, 4, 5]) | |||
y = np.array([2, 3, 4, 4, 5]) | |||
n = len(x) | |||
X = np.vstack([x, np.ones(n)]).T | |||
a = np.linalg.lstsq(X, y)[0] | |||
# Plot the data along with the fitted line: | |||
plot(x, y, 'o', label='Original data', markersize=10) | |||
plot(x, np.dot(X,a), 'r', label='Fitted line') | |||
xlabel('x values') | |||
ylabel('y values') | |||
title('Linear regression of y on x') | |||
grid('on') | |||
xlim([0.9, 5.1]) | |||
ylim([1.9, 5.1]) | |||
legend(loc=0) | |||
# Additional calculations | |||
resids = y - np.dot(X,a) # e = y - Xa; | |||
RSS = sum(resids**2) # residual sum of squares | |||
TSS = sum((y - np.mean(y))**2) # total sum of squares | |||
R2 = 1 - RSS/TSS | |||
std_error = np.sqrt(RSS/(n-len(a))) | |||
std_y = np.sqrt(TSS/(n-1)) # just the same as std(y) | |||
R2_adj = 1 - (std_error/std_y)**2 | |||
</syntaxhighlight> | |||
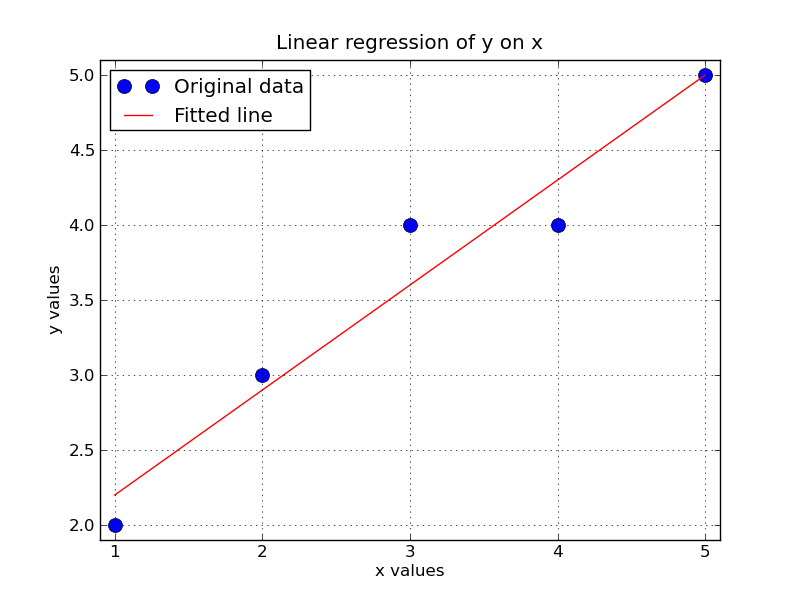
[[Image:Least-squares-Python.png | 550px]] | |||
|} | |} | ||
Revision as of 20:14, 1 December 2010
One of the best packages for fitting least squares models, in addition to all sorts of other statistical manipulation of data is the R language. The following pages from the 4C3 (Statistics for Engineering) website will help you:
However, here is a tutorial on how you can use MATLAB or Python to fit a least squares model.
- MATLAB: use the regress.m and regstats.m function
- Python: use the numpy.linalg.lstsq function
| MATLAB | Python |
|---|---|
x = [1, 2, 3, 4, 5];
y = [2, 3, 4, 4, 5];
y = y(:);
n = numel(x);
X = [ones(n,1) x(:)];
a = regress(y, X) % Contains a_0=a(1) and a_1=a(2)
plot(x, y, 'o')
hold('on')
grid('on')
plot(x, X*a, 'r')
xlabel('x values')
ylabel('y values')
title('Linear regression of y on x')
xlim([0.9, 5.1])
ylim([1.9, 5.1])
legend({'Original data', 'Fitted line'}, 'Location', 'Best')
% Additional calculations
resids = y - X*a; % resids = e = y - Xa
RSS = resids' * resids; % residual sum of squares
TSS = sum((y - mean(y)).^2); % total sum of squares
R2 = 1 - RSS/TSS;
std_error = sqrt(RSS/(n-numel(a)));
std_y = sqrt(TSS/(n-1)); % just the same as std(y)
R2_adj = 1 - (std_error/std_y)^2
|
import numpy as np
from matplotlib.pyplot import *
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 4, 4, 5])
n = len(x)
X = np.vstack([x, np.ones(n)]).T
a = np.linalg.lstsq(X, y)[0]
# Plot the data along with the fitted line:
plot(x, y, 'o', label='Original data', markersize=10)
plot(x, np.dot(X,a), 'r', label='Fitted line')
xlabel('x values')
ylabel('y values')
title('Linear regression of y on x')
grid('on')
xlim([0.9, 5.1])
ylim([1.9, 5.1])
legend(loc=0)
# Additional calculations
resids = y - np.dot(X,a) # e = y - Xa;
RSS = sum(resids**2) # residual sum of squares
TSS = sum((y - np.mean(y))**2) # total sum of squares
R2 = 1 - RSS/TSS
std_error = np.sqrt(RSS/(n-len(a)))
std_y = np.sqrt(TSS/(n-1)) # just the same as std(y)
R2_adj = 1 - (std_error/std_y)**2
|