Software tutorial/Least squares modelling (linear regression)
One of the best packages for fitting least squares models, in addition to all sorts of other statistical manipulation of data is the R language. The following pages from the 4C3 (Statistics for Engineering) website will help you:
However, here is a tutorial on how you can use MATLAB or Python to fit a least squares model.
- MATLAB: use the regress.m and regstats.m function
- Python: use the numpy.linalg.lstsq function
Single-variable regression
| MATLAB | Python |
|---|---|
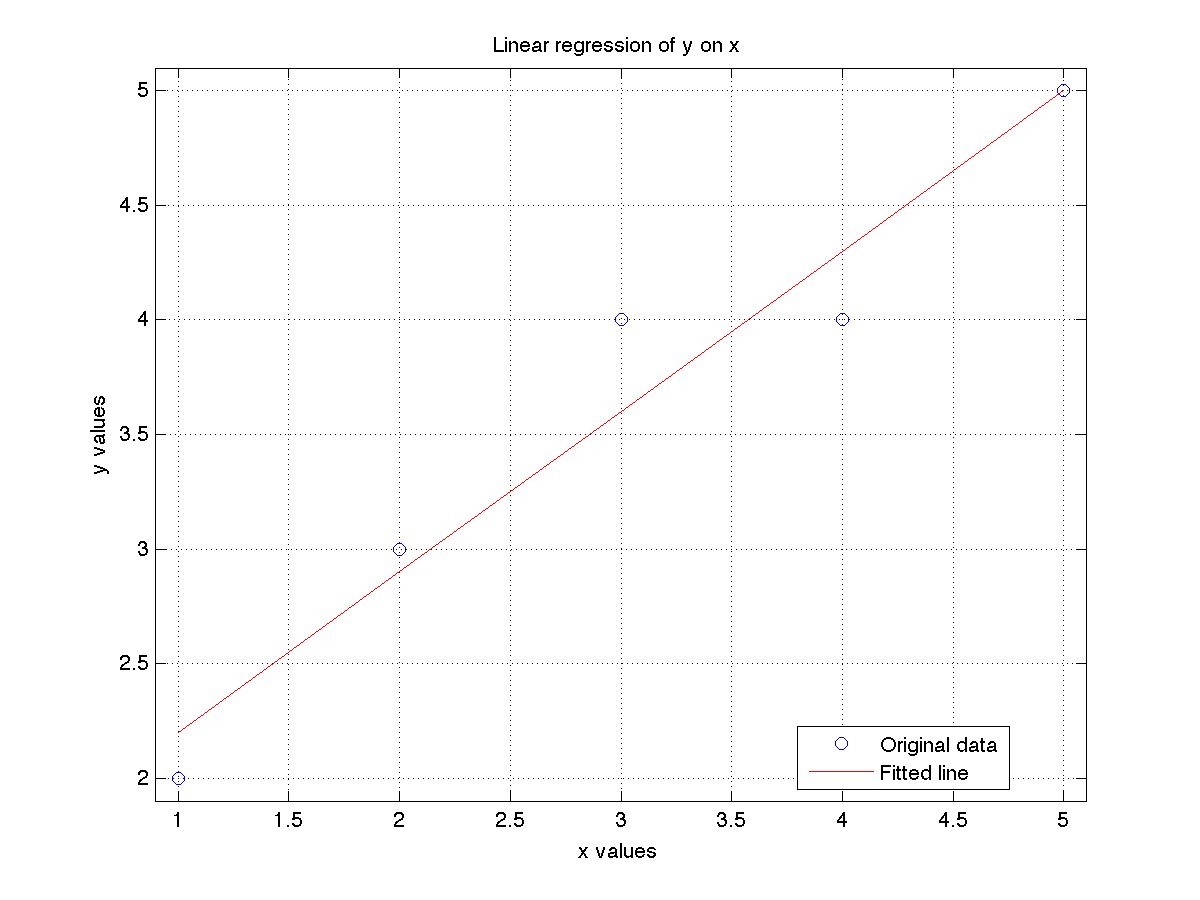
x = [1, 2, 3, 4, 5];
y = [2, 3, 4, 4, 5];
y = y(:);
n = numel(x);
X = [ones(n,1) x(:)];
a = regress(y, X) % Contains a_0=a(1) and a_1=a(2)
plot(x, y, 'o')
hold('on')
grid('on')
plot(x, X*a, 'r')
xlabel('x values')
ylabel('y values')
title('Linear regression of y on x')
xlim([0.9, 5.1])
ylim([1.9, 5.1])
legend({'Original data', 'Fitted line'}, 'Location', 'Best')
% Additional calculations
resids = y - X*a; % resids = e = y - Xa
RSS = resids' * resids; % residual sum of squares
TSS = sum((y - mean(y)).^2); % total sum of squares
R2 = 1 - RSS/TSS;
std_error = sqrt(RSS/(n-numel(a)));
std_y = sqrt(TSS/(n-1)); % just the same as std(y)
R2_adj = 1 - (std_error/std_y)^2
|
import numpy as np
from matplotlib.pyplot import *
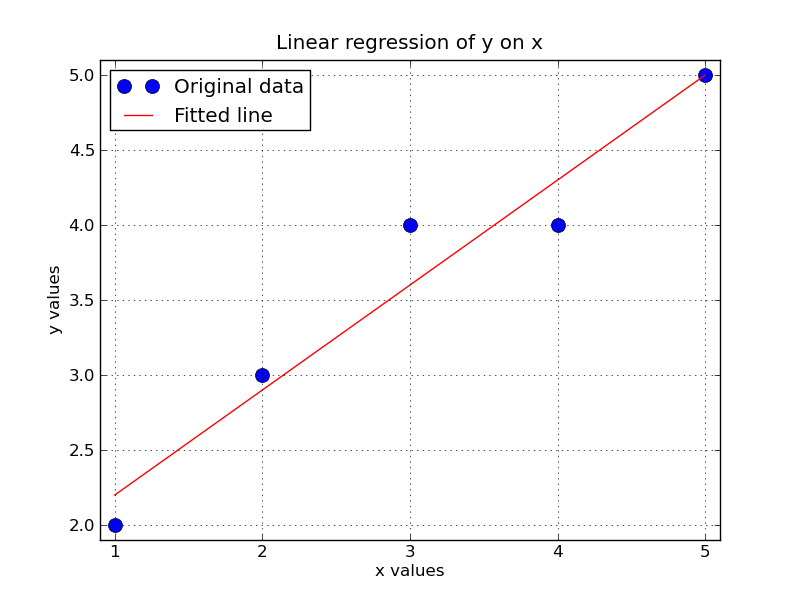
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 4, 4, 5])
n = len(x)
X = np.vstack([x, np.ones(n)]).T
a = np.linalg.lstsq(X, y)[0]
# Plot the data along with the fitted line:
plot(x, y, 'o', label='Original data', markersize=10)
plot(x, np.dot(X,a), 'r', label='Fitted line')
xlabel('x values')
ylabel('y values')
title('Linear regression of y on x')
grid('on')
xlim([0.9, 5.1])
ylim([1.9, 5.1])
legend(loc=0)
# Additional calculations
resids = y - np.dot(X,a) # e = y - Xa;
RSS = sum(resids**2) # residual sum of squares
TSS = sum((y - np.mean(y))**2) # total sum of squares
R2 = 1 - RSS/TSS
std_error = np.sqrt(RSS/(n-len(a)))
std_y = np.sqrt(TSS/(n-1)) # just the same as std(y)
R2_adj = 1 - (std_error/std_y)**2
|
Matlab provides the function regstats that can be used as follows:
>> regstats(y, x)
to show additional regression statistics. However, all the outputs from a linear model that we require for this course are computed in the code shown above. Python does not have a similar function (to my knowledge).
Multiple linear regression
The case for multiple linear regression is identical to that shown above. The only difference is that you have to expand the X matrix with extra columns. The least squares coefficients in vector a are returned in the same order as the columns in matrix X.