Difference between revisions of "Software tutorial/Integration of ODEs"
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{Navigation|Book=Software tutorial|previous=Creating and saving plots|current=Tutorial index|next=Least squares modelling (linear regression)}} | |||
__TOC__ | |||
= Background = | = Background = | ||
| Line 228: | Line 230: | ||
= Example with coupled ODEs = | = Example with coupled ODEs = | ||
We will now expand our example to a system of two coupled ODEs. Still in the same reactor we are now considering the rate constant to be a function of temperature: \(k = 0.15 e^{- | We will now expand our example to a system of two coupled ODEs. Still in the same reactor we are now considering the rate constant to be a function of temperature: \(k = 0.15 e^{- E_a/(RT)}\) L/(mol.min), with \(E_a = 5000\) J/(mol) and R = \(8.314 \) J/mol.K, and \(T(t)\) is the time-varying tank temperature, measured in Kelvin. Furthermore, the reaction is known to release heat, with \(\Delta H_r = -590\) J/mol. The time-dependent mass and energy balance for this system is now: | ||
\[ \begin{align*}\frac{dC_{\sf A}(t)}{dt} &= \frac{F(t)}{V} \bigg( C_{{\sf A},\text{in}} - C_{\sf A} \bigg) - 0.15 e^{- | \[ \begin{align*}\frac{dC_{\sf A}(t)}{dt} &= \frac{F(t)}{V} \bigg( C_{{\sf A},\text{in}} - C_{\sf A} \bigg) - 0.15 e^{- E_a/(RT)} C_{\sf A}^2 \\ \frac{dT(t)}{dt} &= \frac{F(t)\rho C_p(T)}{V \rho C_p(T)}\bigg(T_\text{in} - T(t) \bigg) - \frac{0.15 e^{- E_a/(RT)} C_{\sf A}^2 V (\Delta H_r)}{V \rho C_p}\end{align*}\] | ||
where \(C_{{\sf A},\text{in}} = 2.5\) mol/L, \(T_\text{in} = 288\) K; we will initially assume constant volume of \(V = 100\) L and constant inlet flow of \(F(t) = 20.1 \) L/min. Also, \(C_p(T) = 4.184 - 0.002 | where \(C_{{\sf A},\text{in}} = 2.5\) mol/L, \(T_\text{in} = 288\) K; we will initially assume constant volume of \(V = 100\) L and constant inlet flow of \(F(t) = 20.1 \) L/min. Also, \(C_p(T) = 4.184 - 0.002(T-273) \) J/(kg.K), the molar heat capacity of the liquid phase system, a weak function of the system temperature. The density of the liquid phase is \(\rho=1.05\) kg/L. We need two initial conditions as well: | ||
* \( C_{\sf A}(t=0) = | * \( C_{\sf A}(t=0) = 0.5\) mol/L | ||
* \(T(t=0) = 295 K \) | * \(T(t=0) = 295 K \) | ||
| Line 281: | Line 283: | ||
dydt(2) = F/V*(T_in - T) - (Hr*k*CA^2)/(rho*Cp); | dydt(2) = F/V*(T_in - T) - (Hr*k*CA^2)/(rho*Cp); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
In a separate file (any name), for example: ode_driver.m, which will "drive" the ODE solver: | In a separate file (any name), for example: '''<tt>ode_driver.m</tt>''', which will "drive" the ODE solver: | ||
<syntaxhighlight lang="matlab"> | <syntaxhighlight lang="matlab"> | ||
% Integrate the ODE | % Integrate the ODE | ||
| Line 295: | Line 297: | ||
% Integrate the ODE(s): | % Integrate the ODE(s): | ||
[t, y] = | [t, y] = ode45(@tank_coupled, [t_start, t_final], ... | ||
[CA_t_zero, T_t_zero]); | |||
% Plot the results: | % Plot the results: | ||
| Line 416: | Line 419: | ||
|} | |} | ||
* | ;'''Important notes''' | ||
* | |||
** | :* Each trajectory (ODE) must have an initial condition. | ||
** algebraic | :* The function that specifies the ODE must return a ''column'' vector with \(n\) entries, one for each ODE. | ||
* | :* Algebraic equations may be included in the ODE function. For example: | ||
:** \(C_p = 4.184 - 0.002(T-273)\) is an algebraic function | |||
:** If the inlet flow varied over time according to \(F(t) = 20.1 + 2\sin(t)\) then this algebraic equation could be added. | |||
:* Numerical integration allows for discontinuities. For example, a step input at \(t=50\) minutes in the inlet flow can be coded as | |||
:: | |||
<syntaxhighlight lang="matlab"> | |||
if t < 50 | |||
F = 20.1 | |||
else | |||
F = 25.1 | |||
end | |||
</syntaxhighlight> | |||
{{Navigation|Book=Software tutorial|previous=Creating and saving plots|current=Tutorial index|next=Least squares modelling (linear regression)}} | |||
Latest revision as of 20:49, 2 December 2010
Background
In our course we have learned several ways of integrating a single equation \(\displaystyle \frac{dy(t)}{dt} = f(t, y) \) with a given initial condition \(y(t=0)=y_0\); and we have shown that a system of \(n\) first order ODE's can be integrated: \[ \displaystyle \frac{d{\bf y}(t)}{dt} = {\bf f}(t, {\bf y}) \]given a set of \(n\) initial conditions \({\bf y}(t=0) = {\bf y}_0\), i.e. \( {\bf y}_0\) is an \(n \times 1\) vector. The course notes covered Euler's method, Heun's method and Runge-Kutta methods.
However, we only coded Euler's method (because it was simple!), but not the others. These other methods have been (reliably) coded in software packages and sophisticated error correction tools built into their algorithms. You should always use these toolbox functions to integrate your differential equation models. In this section we will show how to use MATLAB and Python's built-in functions to integrate:
- a single differential equation
- a system of differential and algebraic equations.
We will only look at initial value problems (IVPs) in this tutorial.
MATLAB
MATLAB's has several ODE solvers available. You can read up more about the implementation details in this technical document.
Python
Like MATLAB, several integrators are available in Python. The integrator I will use in this tutorial is one of the most recent additions to SciPy - the VODE integrator developed at Lawrence Livermore National Laboratories in 1988. It is a good general-purpose solver for both stiff and non-stiff systems.
NOTE: we will use the superior vode Python integrator - it requires a little more code than the other built-in Python integrator, based on lsodea.
Example problem
The example we will work with is a common modelling reaction: a liquid-based stirred tank reactor, with (initially) constant physical properties, a second order chemical reaction where species A is converted to B according to \({\sf A} \rightarrow {\sf B} \), with reaction rate \(r = k C_{\sf A}^2\). One can find the time-dependent mass balance for this system to be:
\[ \frac{dC_{\sf A}(t)}{dt} = \frac{F(t)}{V} \bigg( C_{{\sf A},\text{in}} - C_{\sf A} \bigg) - k C_{\sf A}^2 \]
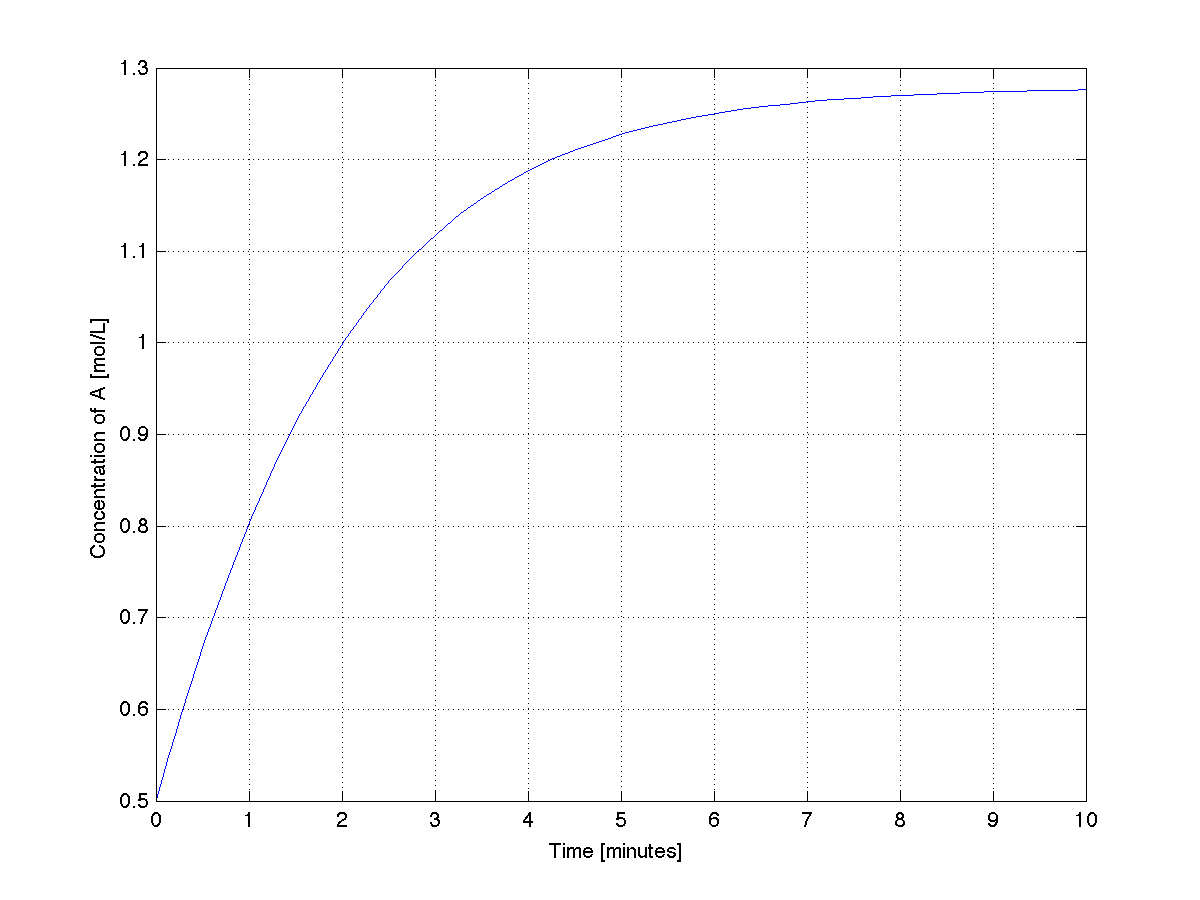
where \(C_{{\sf A},\text{in}} = 5.5\) mol/L, we will initially assume constant volume of \(V = 100\) L and constant inlet flow of \(F(t) = 20.1 \) L/min. The reaction rate constant is 0.15 \(\frac{\text{L}}{\text{mol}.\text{min}}\). We must specify an initial condition for every differential equation: we will let \( C_{\sf A}(t=0) = 0.5\) mol/L.
In the code below we will integrate the ODE from \(t_\text{start} = 0.0\) minutes up to \(t_\text{final} = 10.0\) minutes and plot the time-varying trajectory of concentration in the tank.
The reason for the longer Python code is because we have to constructe the vectors that store the time variable and the corresponding concentration output (as a function of that time variable). The MATLAB code builds this vector for us. MATLAB's vectors are very well suited to plotting, but there is a feature that may not be 100% useful:
| MATLAB | Python |
|---|---|
|
Let's take a look at the MATLAB output: >> t(1:10)
ans =
0
0.0689
0.1378
0.2067
0.2757
0.5257
0.7757
1.0257
1.2757
1.5257
>> y(1:10)
ans =
0.5000
0.5248
0.5490
0.5726
0.5956
0.6742
0.7452
0.8090
0.8662
0.9171
MATLAB places the points at unequal step sizes of time. This is what their documentation has to say:
|
Let's take a look at the Python output: >>> t[0:10]
array([[ 0. ],
[ 0.1],
[ 0.2],
[ 0.3],
[ 0.4],
[ 0.5],
[ 0.6],
[ 0.7],
[ 0.8],
[ 0.9]])
>>> CA[0:10]
array([[ 0.5 ],
[ 0.53581076],
[ 0.57035065],
[ 0.60362937],
[ 0.63566104],
[ 0.66646269],
[ 0.69605419],
[ 0.7244578 ],
[ 0.75169755],
[ 0.77779875]]
The evenly spaced periods of time were by design - see the Python code above. After reading the MATLAB description alongside, you might think the Python integration is inaccurate. This is not true: the Python code we have used here will take multiple steps, of variable size, within each of the delta_t time steps we specified, but the code will only report the values at the boundaries of each delta_t, not the intermediate values. |
Example with coupled ODEs
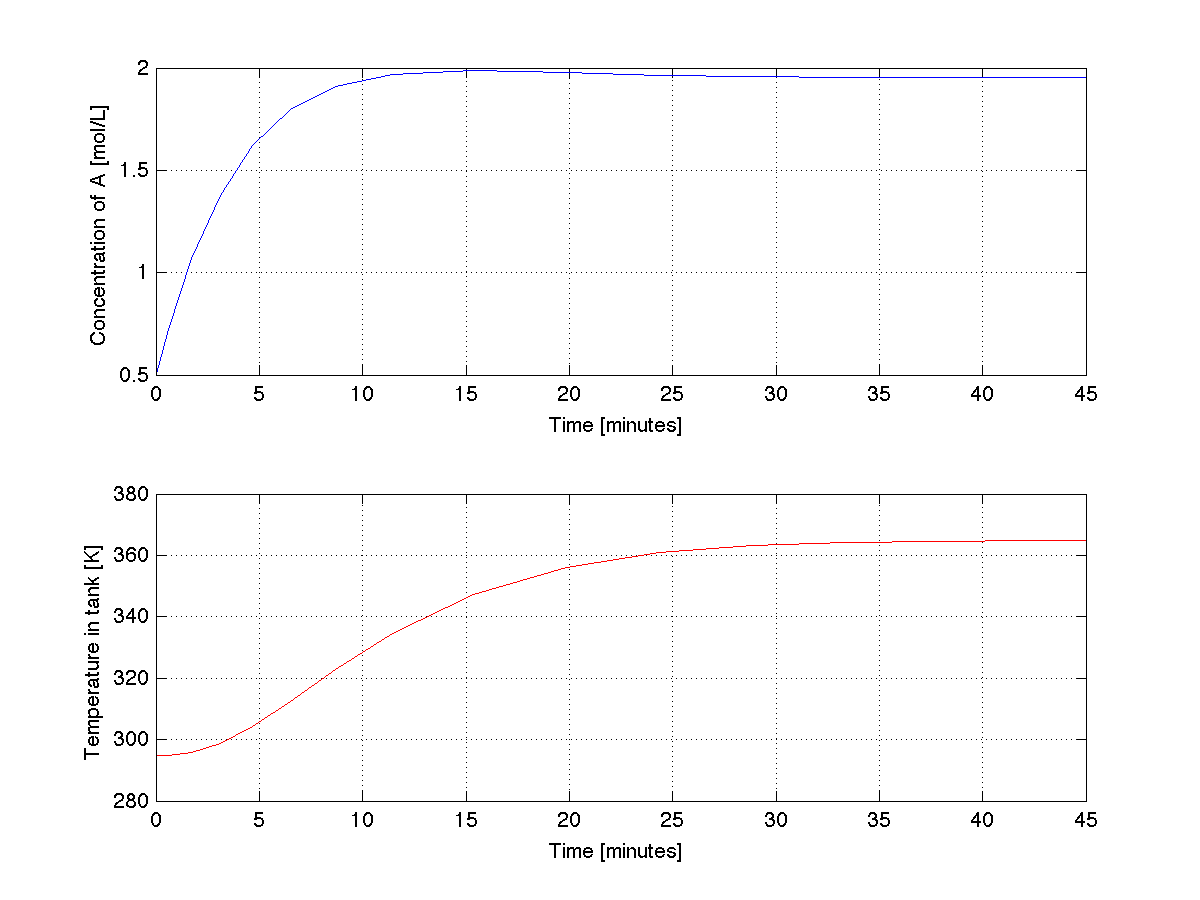
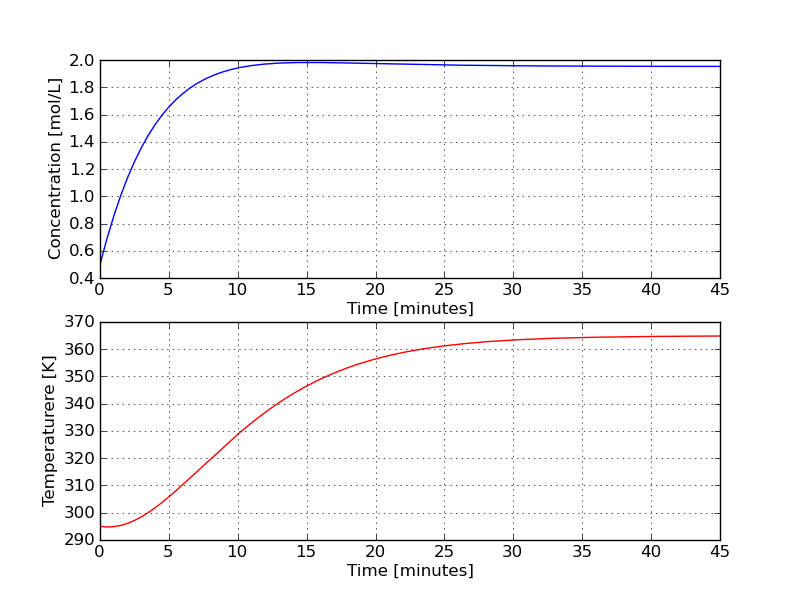
We will now expand our example to a system of two coupled ODEs. Still in the same reactor we are now considering the rate constant to be a function of temperature: \(k = 0.15 e^{- E_a/(RT)}\) L/(mol.min), with \(E_a = 5000\) J/(mol) and R = \(8.314 \) J/mol.K, and \(T(t)\) is the time-varying tank temperature, measured in Kelvin. Furthermore, the reaction is known to release heat, with \(\Delta H_r = -590\) J/mol. The time-dependent mass and energy balance for this system is now:
\[ \begin{align*}\frac{dC_{\sf A}(t)}{dt} &= \frac{F(t)}{V} \bigg( C_{{\sf A},\text{in}} - C_{\sf A} \bigg) - 0.15 e^{- E_a/(RT)} C_{\sf A}^2 \\ \frac{dT(t)}{dt} &= \frac{F(t)\rho C_p(T)}{V \rho C_p(T)}\bigg(T_\text{in} - T(t) \bigg) - \frac{0.15 e^{- E_a/(RT)} C_{\sf A}^2 V (\Delta H_r)}{V \rho C_p}\end{align*}\]
where \(C_{{\sf A},\text{in}} = 2.5\) mol/L, \(T_\text{in} = 288\) K; we will initially assume constant volume of \(V = 100\) L and constant inlet flow of \(F(t) = 20.1 \) L/min. Also, \(C_p(T) = 4.184 - 0.002(T-273) \) J/(kg.K), the molar heat capacity of the liquid phase system, a weak function of the system temperature. The density of the liquid phase is \(\rho=1.05\) kg/L. We need two initial conditions as well:
- \( C_{\sf A}(t=0) = 0.5\) mol/L
- \(T(t=0) = 295 K \)
In the code below we will integrate the ODE from \(t_\text{start} = 0.0\) minutes up to \(t_\text{final} = 45.0\) minutes and plot the time-varying trajectory of concentration in the tank.
- Important notes
- Each trajectory (ODE) must have an initial condition.
- The function that specifies the ODE must return a column vector with \(n\) entries, one for each ODE.
- Algebraic equations may be included in the ODE function. For example:
- \(C_p = 4.184 - 0.002(T-273)\) is an algebraic function
- If the inlet flow varied over time according to \(F(t) = 20.1 + 2\sin(t)\) then this algebraic equation could be added.
- Numerical integration allows for discontinuities. For example, a step input at \(t=50\) minutes in the inlet flow can be coded as
if t < 50
F = 20.1
else
F = 25.1
end