Difference between revisions of "Software tutorial/Integration of ODEs"
m |
|||
| (43 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
In our course we have learned several ways of integrating a single equation \(\frac{dy(t)}{dt} = f(t, y) \) with a given initial condition \(y(t=0)=y_0\). | {{Navigation|Book=Software tutorial|previous=Creating and saving plots|current=Tutorial index|next=Least squares modelling (linear regression)}} | ||
__TOC__ | |||
= Background = | |||
In our course we have learned several ways of integrating a single equation \(\displaystyle \frac{dy(t)}{dt} = f(t, y) \) with a given initial condition \(y(t=0)=y_0\); and we have shown that a system of \(n\) first order ODE's can be integrated: \[ \displaystyle \frac{d{\bf y}(t)}{dt} = {\bf f}(t, {\bf y}) \]given a set of \(n\) initial conditions \({\bf y}(t=0) = {\bf y}_0\), i.e. \( {\bf y}_0\) is an \(n \times 1\) vector. The [[Ordinary_differential_equations | course notes covered]] Euler's method, Heun's method and Runge-Kutta methods. | |||
However, we only coded Euler's method (because it was simple!), but not the others. These other methods have been (reliably) coded in software packages and sophisticated error correction tools built into their algorithms. You should always use these toolbox functions to integrate your differential equation models. In this section we will show how to use MATLAB and Python's built-in functions to integrate: | |||
* a single differential equation | |||
* a system of differential and algebraic equations. | |||
We will only look at initial value problems (IVPs) in this tutorial. | |||
== MATLAB == | |||
MATLAB's has [http://www.mathworks.com/help/techdoc/ref/ode45.html several ODE solvers available]. You can read up more about the implementation details in [http://www.mathworks.com/help/pdf_doc/otherdocs/ode_suite.pdf this technical document]. | |||
== Python == | |||
Like MATLAB, several integrators are available in Python. The integrator I will use in this tutorial is one of the most recent additions to SciPy - the [https://computation.llnl.gov/casc/nsde/pubs/207532.pdf VODE integrator] developed at Lawrence Livermore National Laboratories in 1988. It is a good general-purpose solver for both stiff and non-stiff systems. | |||
'''NOTE''': we will use the superior <tt>vode</tt> Python integrator - it requires a little more code than the other built-in Python integrator, based on <tt>lsodea</tt>. | |||
= Example problem = | |||
The example we will work with is a common modelling reaction: a liquid-based stirred tank reactor, with (initially) constant physical properties, a second order chemical reaction where species A is converted to B according to \({\sf A} \rightarrow {\sf B} \), with reaction rate \(r = k C_{\sf A}^2\). One can find the time-dependent mass balance for this system to be: | |||
\[ \frac{dC_{\sf A}(t)}{dt} = \frac{F(t)}{V} \bigg( C_{{\sf A},\text{in}} - C_{\sf A} \bigg) - k C_{\sf A}^2 \] | |||
where \(C_{{\sf A},\text{in}} = 5.5\) mol/L, we will initially assume constant volume of \(V = 100\) L and constant inlet flow of \(F(t) = 20.1 \) L/min. The reaction rate constant is 0.15 \(\frac{\text{L}}{\text{mol}.\text{min}}\). We must specify an initial condition for every differential equation: we will let \( C_{\sf A}(t=0) = 0.5\) mol/L. | |||
In the code below we will integrate the ODE from \(t_\text{start} = 0.0\) minutes up to \(t_\text{final} = 10.0\) minutes and plot the time-varying trajectory of concentration in the tank. | |||
{| class="wikitable" | |||
|- | |||
! MATLAB | |||
! Python | |||
|- | |||
| width="50%" valign="top" | | |||
In a file called '''<tt>tank.m</tt>''': | |||
<syntaxhighlight lang="matlab"> | |||
function dydt = tank(t, y) | |||
% Dynamic balance for a CSTR | |||
% | |||
% C_A = y(1) = the concentration of A in the tank, mol/L | |||
% | |||
% Returns dy/dt = F/V*(C_{A,in} - C_A) - k*C_A^2 | |||
F = 20.1; % L/min | |||
CA_in = 2.5; % mol/L | |||
V = 100; % L | |||
k = 0.150; % L/(min.mol) | |||
% Assign some variables for convenience of notation | |||
CA = y(1); | |||
% The output from the ODE function must be a COLUMN vector, | |||
% with n rows | |||
n = numel(y); % How many ODE's in this system? | |||
dydt = zeros(n,1); | |||
dydt(1) = F/V*(CA_in - CA) - k*CA^2; | |||
</syntaxhighlight> | |||
In a separate file (any name), for example: '''<tt>ode_driver.m</tt>''', which will "drive" the ODE solver: | |||
<syntaxhighlight lang="matlab"> | |||
% Integrate the ODE | |||
% ----------------- | |||
% Set the time range: | |||
t_start = 0; | |||
t_final = 10.0; | |||
% Set the initial condition(s): | |||
CA_t_zero = 0.5; | |||
% Integrate the ODE(s): | |||
[t, y] = ode45(@tank, [t_start, t_final], [CA_t_zero]); | |||
% Plot the results: | |||
clf; | |||
plot(t, y) | |||
grid('on') | |||
xlabel('Time [minutes]') | |||
ylabel('Concentration of A [mol/L]') | |||
</syntaxhighlight> | |||
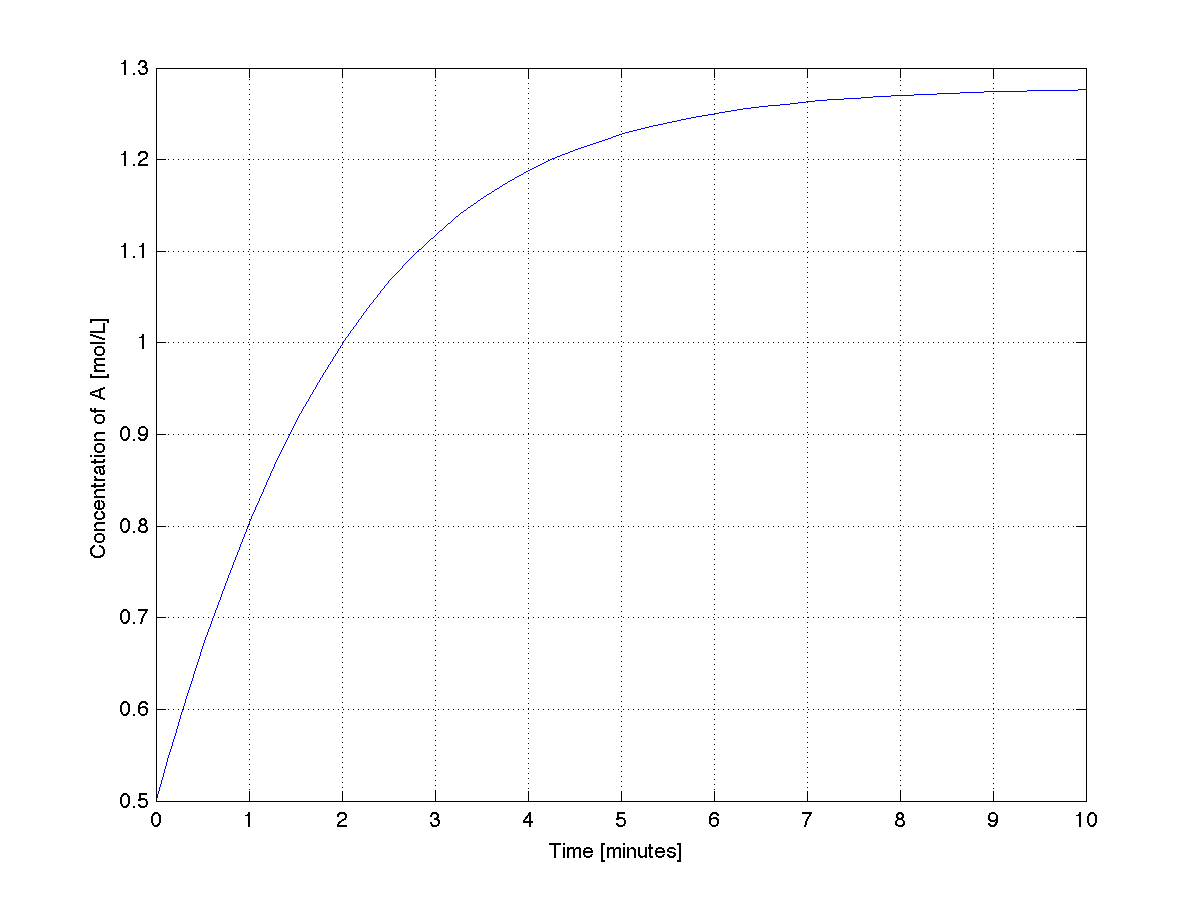
A plot from this code shows the system stabilizing after about 9 minutes. | |||
[[Image:Single-ode-MATLAB.png | 550px]] | |||
| width="50%" valign="top" | | |||
<syntaxhighlight lang="python"> | |||
import numpy as np | |||
from scipy import integrate | |||
from matplotlib.pylab import * | |||
def tank(t, y): | |||
""" | |||
Dynamic balance for a CSTR | |||
C_A = y[0] = the concentration of A in the tank, mol/L | |||
Returns dy/dt = F/V*(C_{A,in} - C_A) - k*C_A^2 | |||
""" | |||
F = 20.1 # L/min | |||
CA_in = 2.5 # mol/L | |||
V = 100 # L | |||
k = 0.15 # L/(mol.min) | |||
# Assign some variables for convenience of notation | |||
CA = y[0] | |||
# Output from ODE function must be a COLUMN vector, with n rows | |||
n = len(y) # 1: implies its a single ODE | |||
dydt = np.zeros((n,1)) | |||
dydt[0] = F/V*(CA_in - CA) - k*CA**2 | |||
return dydt | |||
# The ``driver`` that will integrate the ODE(s): | |||
if __name__ == '__main__': | |||
# Start by specifying the integrator: | |||
# use ``vode`` with "backward differentiation formula" | |||
r = integrate.ode(tank).set_integrator('vode', method='bdf') | |||
# Set the time range | |||
t_start = 0.0 | |||
t_final = 10.0 | |||
delta_t = 0.1 | |||
# Number of time steps: 1 extra for initial condition | |||
num_steps = np.floor((t_final - t_start)/delta_t) + 1 | |||
# Set initial condition(s): for integrating variable and time! | |||
CA_t_zero = 0.5 | |||
r.set_initial_value([CA_t_zero], t_start) | |||
# Additional Python step: create vectors to store trajectories | |||
t = np.zeros((num_steps, 1)) | |||
CA = np.zeros((num_steps, 1)) | |||
t[0] = t_start | |||
CA[0] = CA_t_zero | |||
# Integrate the ODE(s) across each delta_t timestep | |||
k = 1 | |||
while r.successful() and k < num_steps: | |||
r.integrate(r.t + delta_t) | |||
# Store the results to plot later | |||
t[k] = r.t | |||
CA[k] = r.y[0] | |||
k += 1 | |||
# All done! Plot the trajectories: | |||
plot(t, CA) | |||
grid('on') | |||
xlabel('Time [minutes]') | |||
ylabel('Concentration [mol/L]') | |||
</syntaxhighlight> | |||
[[Image:Single-ode-Python.png|550px]] | |||
|} | |||
The reason for the longer Python code is because we have to constructe the vectors that store the time variable and the corresponding concentration output (as a function of that time variable). The MATLAB code builds this vector for us. MATLAB's vectors are very well suited to plotting, but there is a feature that may not be 100% useful: | |||
{| class="wikitable" | |||
|- | |||
! MATLAB | |||
! Python | |||
|- | |||
| width="50%" valign="top" | | |||
Let's take a look at the MATLAB output: | |||
<syntaxhighlight lang="matlab"> | |||
>> t(1:10) | |||
ans = | |||
0 | |||
0.0689 | |||
0.1378 | |||
0.2067 | |||
0.2757 | |||
0.5257 | |||
0.7757 | |||
1.0257 | |||
1.2757 | |||
1.5257 | |||
>> y(1:10) | |||
ans = | |||
0.5000 | |||
0.5248 | |||
0.5490 | |||
0.5726 | |||
0.5956 | |||
0.6742 | |||
0.7452 | |||
0.8090 | |||
0.8662 | |||
0.9171 | |||
</syntaxhighlight> | |||
MATLAB places the points at unequal step sizes of time. This is what their documentation has to say: | |||
:The MATLAB ODE solvers utilize these methods by taking a step, estimating the error at this step, checking to see if the value is greater than or less than the tolerance, and altering the step size accordingly. These integration methods do not lend themselves to a fixed step size. Using an algorithm that uses a fixed step size is dangerous since you can miss points where your signal frequency is greater than the solver frequency. Using a variable step ensures that a large step size is used for low frequencies and a small step size is used for high frequencies. The ODE solvers within MATLAB are optimized for a variable step, run faster with a variable step size, and clearly the results are more accurate. | |||
| width="50%" valign="top" | | |||
Let's take a look at the Python output: | |||
<syntaxhighlight lang="python"> | |||
>>> t[0:10] | |||
array([[ 0. ], | |||
[ 0.1], | |||
[ 0.2], | |||
[ 0.3], | |||
[ 0.4], | |||
[ 0.5], | |||
[ 0.6], | |||
[ 0.7], | |||
[ 0.8], | |||
[ 0.9]]) | |||
>>> CA[0:10] | |||
array([[ 0.5 ], | |||
[ 0.53581076], | |||
[ 0.57035065], | |||
[ 0.60362937], | |||
[ 0.63566104], | |||
[ 0.66646269], | |||
[ 0.69605419], | |||
[ 0.7244578 ], | |||
[ 0.75169755], | |||
[ 0.77779875]] | |||
</syntaxhighlight> | |||
The evenly spaced periods of time were by design - see the Python code above. After reading the MATLAB description alongside, you might think the Python integration is inaccurate. This is not true: the Python code we have used here will take multiple steps, of variable size, within each of the <tt>delta_t</tt> time steps we specified, but the code will only report the values at the boundaries of each <tt>delta_t</tt>, not the intermediate values. | |||
|} | |||
= Example with coupled ODEs = | |||
We will now expand our example to a system of two coupled ODEs. Still in the same reactor we are now considering the rate constant to be a function of temperature: \(k = 0.15 e^{- E_a/(RT)}\) L/(mol.min), with \(E_a = 5000\) J/(mol) and R = \(8.314 \) J/mol.K, and \(T(t)\) is the time-varying tank temperature, measured in Kelvin. Furthermore, the reaction is known to release heat, with \(\Delta H_r = -590\) J/mol. The time-dependent mass and energy balance for this system is now: | |||
\[ \begin{align*}\frac{dC_{\sf A}(t)}{dt} &= \frac{F(t)}{V} \bigg( C_{{\sf A},\text{in}} - C_{\sf A} \bigg) - 0.15 e^{- E_a/(RT)} C_{\sf A}^2 \\ \frac{dT(t)}{dt} &= \frac{F(t)\rho C_p(T)}{V \rho C_p(T)}\bigg(T_\text{in} - T(t) \bigg) - \frac{0.15 e^{- E_a/(RT)} C_{\sf A}^2 V (\Delta H_r)}{V \rho C_p}\end{align*}\] | |||
where \(C_{{\sf A},\text{in}} = 2.5\) mol/L, \(T_\text{in} = 288\) K; we will initially assume constant volume of \(V = 100\) L and constant inlet flow of \(F(t) = 20.1 \) L/min. Also, \(C_p(T) = 4.184 - 0.002(T-273) \) J/(kg.K), the molar heat capacity of the liquid phase system, a weak function of the system temperature. The density of the liquid phase is \(\rho=1.05\) kg/L. We need two initial conditions as well: | |||
* \( C_{\sf A}(t=0) = 0.5\) mol/L | |||
* \(T(t=0) = 295 K \) | |||
In the code below we will integrate the ODE from \(t_\text{start} = 0.0\) minutes up to \(t_\text{final} = 45.0\) minutes and plot the time-varying trajectory of concentration in the tank. | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 11: | Line 246: | ||
|- | |- | ||
| width="50%" valign="top" | | | width="50%" valign="top" | | ||
The following code appears in an m-file called: '''<tt>tank_coupled.m</tt>''' | |||
<syntaxhighlight lang="matlab"> | |||
function dydt = tank_coupled(t, y) | |||
% Dynamic balance for a CSTR | |||
% C_A = y(1) = the concentration of A in the tank, [mol/L] | |||
% T = y(2) = the tank temperature, [K] | |||
% | |||
% Returns dy/dt = [F/V*(C_{A,in} - C_A) - k*C_A^2 ] | |||
% [F/V*(T_in - T) - k*C_A^2*HR/(rho*Cp) ] | |||
% | |||
F = 20.1; % L/min | |||
CA_in = 2.5; % mol/L | |||
V = 100.0; % L | |||
k0 = 0.15; % L/(mol.min) | |||
Ea = 5000; % J/mol | |||
R = 8.314; % J/(mol.K) | |||
Hr = -590; % J/mol | |||
T_in = 288; % K | |||
rho = 1.050; % kg/L | |||
% Assign some variables for convenience of notation | |||
CA = y(1); | |||
T = y(2); | |||
% Algebraic equations | |||
k = k0 * exp(-Ea/(R*T)); % L/(mol.min) | |||
Cp = 4.184 - 0.002*(T-273); % J/(kg.K) | |||
% The output from the ODE function must be a COLUMN vector, | |||
% with n rows | |||
n = numel(y); % How many ODE's in this system? 2 | |||
dydt = zeros(n,1); | |||
dydt(1) = F/V*(CA_in - CA) - k*CA^2; | |||
dydt(2) = F/V*(T_in - T) - (Hr*k*CA^2)/(rho*Cp); | |||
</syntaxhighlight> | |||
In a separate file (any name), for example: '''<tt>ode_driver.m</tt>''', which will "drive" the ODE solver: | |||
<syntaxhighlight lang="matlab"> | |||
% Integrate the ODE | |||
% ----------------- | |||
% Set the time range: | |||
t_start = 0; | |||
t_final = 45.0; | |||
% Set the initial condition(s): | |||
CA_t_zero = 0.5; | |||
T_t_zero = 295; | |||
% Integrate the ODE(s): | |||
[t, y] = ode45(@tank_coupled, [t_start, t_final], ... | |||
[CA_t_zero, T_t_zero]); | |||
% Plot the results: | |||
clf; | |||
subplot(2, 1, 1) | |||
plot(t, y(:,1)) | |||
xlabel('Time [minutes]') | |||
ylabel('Concentration of A [mol/L]') | |||
grid('on') | |||
subplot(2, 1, 2) | |||
plot(t, y(:,2), 'r') | |||
xlabel('Time [minutes]') | |||
ylabel('Temperature in tank [K]') | |||
grid('on') | |||
print('-dpng', 'coupled-ode-MATLAB.png') | |||
</syntaxhighlight> | |||
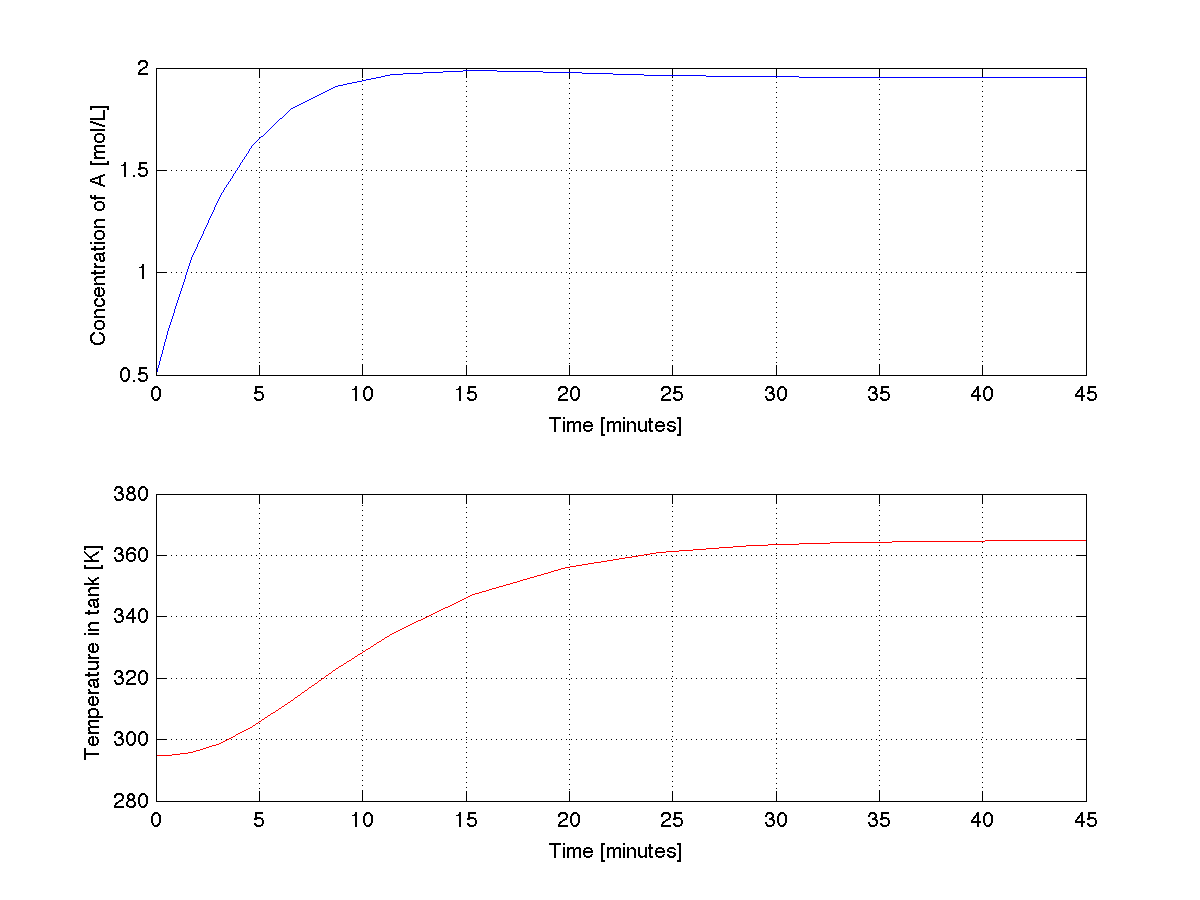
The trajectories produced by the above code are shown below. Do they make engineering sense? | |||
[[Image:Coupled-ode-MATLAB.png | 550px]] | |||
| width="50%" valign="top" | | | width="50%" valign="top" | | ||
<syntaxhighlight lang="python"> | |||
import numpy as np | |||
from scipy import integrate | |||
from matplotlib.pylab import * | |||
def tank(t, y): | |||
""" | |||
Dynamic balance for a CSTR | |||
C_A = y[0] = the concentration of A in the tank, [mol/L] | |||
T = y[1] = the tank temperature, [K] | |||
Returns dy/dt = [F/V*(C_{A,in} - C_A) - k*C_A^2 ] | |||
[F/V*(T_in - T) - k*C_A^2*HR/(rho*Cp) ] | |||
""" | |||
F = 20.1 # L/min | |||
CA_in = 2.5 # mol/L | |||
V = 100.0 # L | |||
k0 = 0.15 # L/(mol.min) | |||
Ea = 5000 # J/mol | |||
R = 8.314 # J/(mol.K) | |||
Hr = -590 # J/mol | |||
T_in = 288 # K | |||
rho = 1.050 # kg/L | |||
# Assign some variables for convenience of notation | |||
CA = y[0] | |||
T = y[1] | |||
# Algebraic equations | |||
k = k0 * np.exp(-Ea/(R*T)) # L/(mol.min) | |||
Cp = 4.184 - 0.002*(T-273) # J/(kg.K) | |||
# Output from ODE function must be a COLUMN vector, with n rows | |||
n = len(y) # 2: implies we have two ODEs | |||
dydt = np.zeros((n,1)) | |||
dydt[0] = F/V*(CA_in - CA) - k*CA**2 | |||
dydt[1] = F/V*(T_in - T) - (Hr*k*CA**2)/(rho*Cp) | |||
return dydt | |||
# The ``driver`` that will integrate the ODE(s): | |||
if __name__ == '__main__': | |||
# Start by specifying the integrator: | |||
# use ``vode`` with "backward differentiation formula" | |||
r = integrate.ode(tank).set_integrator('vode', method='bdf') | |||
# Set the time range | |||
t_start = 0.0 | |||
t_final = 45.0 | |||
delta_t = 0.1 | |||
# Number of time steps: 1 extra for initial condition | |||
num_steps = np.floor((t_final - t_start)/delta_t) + 1 | |||
# Set initial condition(s): for integrating variable and time! | |||
CA_t_zero = 0.5 | |||
T_t_zero = 295.0 | |||
r.set_initial_value([CA_t_zero, T_t_zero], t_start) | |||
# Additional Python step: create vectors to store trajectories | |||
t = np.zeros((num_steps, 1)) | |||
CA = np.zeros((num_steps, 1)) | |||
temp = np.zeros((num_steps, 1)) | |||
t[0] = t_start | |||
CA[0] = CA_t_zero | |||
temp[0] = T_t_zero | |||
# Integrate the ODE(s) across each delta_t timestep | |||
k = 1 | |||
while r.successful() and k < num_steps: | |||
r.integrate(r.t + delta_t) | |||
# Store the results to plot later | |||
t[k] = r.t | |||
CA[k] = r.y[0] | |||
temp[k] = r.y[1] | |||
k += 1 | |||
# All done! Plot the trajectories in two separate plots: | |||
fig = figure() | |||
ax1 = subplot(211) | |||
ax1.plot(t, CA) | |||
ax1.set_xlim(t_start, t_final) | |||
ax1.set_xlabel('Time [minutes]') | |||
ax1.set_ylabel('Concentration [mol/L]') | |||
ax1.grid('on') | |||
ax2 = plt.subplot(212) | |||
ax2.plot(t, temp, 'r') | |||
ax2.set_xlim(t_start, t_final) | |||
ax2.set_xlabel('Time [minutes]') | |||
ax2.set_ylabel('Temperaturere [K]') | |||
ax2.grid('on') | |||
fig.savefig('coupled-ode-Python.png') | |||
</syntaxhighlight> | |||
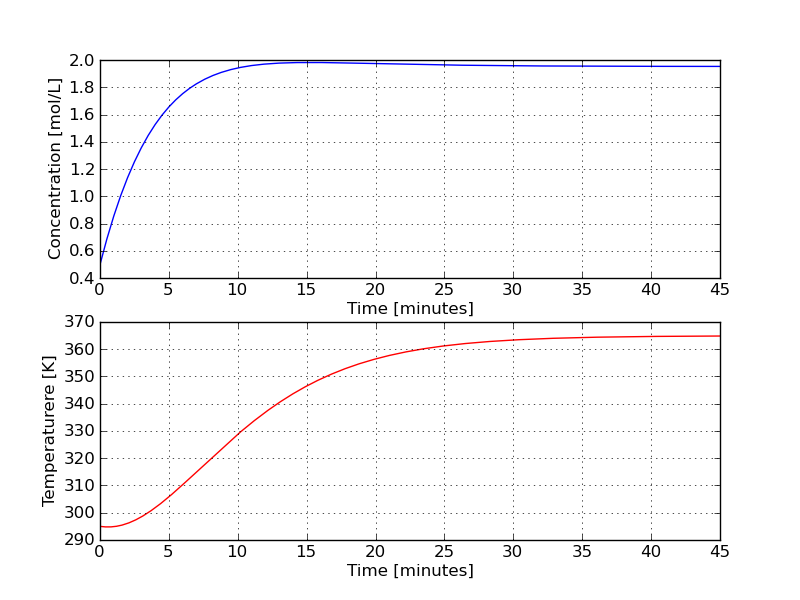
The trajectories produced by the above code are shown below. Do they make engineering sense? | |||
[[Image:Coupled-ode-Python.png | 550px]] | |||
|} | |} | ||
;'''Important notes''' | |||
:* Each trajectory (ODE) must have an initial condition. | |||
:* The function that specifies the ODE must return a ''column'' vector with \(n\) entries, one for each ODE. | |||
:* Algebraic equations may be included in the ODE function. For example: | |||
:** \(C_p = 4.184 - 0.002(T-273)\) is an algebraic function | |||
:** If the inlet flow varied over time according to \(F(t) = 20.1 + 2\sin(t)\) then this algebraic equation could be added. | |||
:* Numerical integration allows for discontinuities. For example, a step input at \(t=50\) minutes in the inlet flow can be coded as | |||
:: | |||
<syntaxhighlight lang="matlab"> | |||
if t < 50 | |||
F = 20.1 | |||
else | |||
F = 25.1 | |||
end | |||
</syntaxhighlight> | |||
{{Navigation|Book=Software tutorial|previous=Creating and saving plots|current=Tutorial index|next=Least squares modelling (linear regression)}} | |||
Latest revision as of 20:49, 2 December 2010
Background
In our course we have learned several ways of integrating a single equation \(\displaystyle \frac{dy(t)}{dt} = f(t, y) \) with a given initial condition \(y(t=0)=y_0\); and we have shown that a system of \(n\) first order ODE's can be integrated: \[ \displaystyle \frac{d{\bf y}(t)}{dt} = {\bf f}(t, {\bf y}) \]given a set of \(n\) initial conditions \({\bf y}(t=0) = {\bf y}_0\), i.e. \( {\bf y}_0\) is an \(n \times 1\) vector. The course notes covered Euler's method, Heun's method and Runge-Kutta methods.
However, we only coded Euler's method (because it was simple!), but not the others. These other methods have been (reliably) coded in software packages and sophisticated error correction tools built into their algorithms. You should always use these toolbox functions to integrate your differential equation models. In this section we will show how to use MATLAB and Python's built-in functions to integrate:
- a single differential equation
- a system of differential and algebraic equations.
We will only look at initial value problems (IVPs) in this tutorial.
MATLAB
MATLAB's has several ODE solvers available. You can read up more about the implementation details in this technical document.
Python
Like MATLAB, several integrators are available in Python. The integrator I will use in this tutorial is one of the most recent additions to SciPy - the VODE integrator developed at Lawrence Livermore National Laboratories in 1988. It is a good general-purpose solver for both stiff and non-stiff systems.
NOTE: we will use the superior vode Python integrator - it requires a little more code than the other built-in Python integrator, based on lsodea.
Example problem
The example we will work with is a common modelling reaction: a liquid-based stirred tank reactor, with (initially) constant physical properties, a second order chemical reaction where species A is converted to B according to \({\sf A} \rightarrow {\sf B} \), with reaction rate \(r = k C_{\sf A}^2\). One can find the time-dependent mass balance for this system to be:
\[ \frac{dC_{\sf A}(t)}{dt} = \frac{F(t)}{V} \bigg( C_{{\sf A},\text{in}} - C_{\sf A} \bigg) - k C_{\sf A}^2 \]
where \(C_{{\sf A},\text{in}} = 5.5\) mol/L, we will initially assume constant volume of \(V = 100\) L and constant inlet flow of \(F(t) = 20.1 \) L/min. The reaction rate constant is 0.15 \(\frac{\text{L}}{\text{mol}.\text{min}}\). We must specify an initial condition for every differential equation: we will let \( C_{\sf A}(t=0) = 0.5\) mol/L.
In the code below we will integrate the ODE from \(t_\text{start} = 0.0\) minutes up to \(t_\text{final} = 10.0\) minutes and plot the time-varying trajectory of concentration in the tank.
The reason for the longer Python code is because we have to constructe the vectors that store the time variable and the corresponding concentration output (as a function of that time variable). The MATLAB code builds this vector for us. MATLAB's vectors are very well suited to plotting, but there is a feature that may not be 100% useful:
| MATLAB | Python |
|---|---|
|
Let's take a look at the MATLAB output: >> t(1:10)
ans =
0
0.0689
0.1378
0.2067
0.2757
0.5257
0.7757
1.0257
1.2757
1.5257
>> y(1:10)
ans =
0.5000
0.5248
0.5490
0.5726
0.5956
0.6742
0.7452
0.8090
0.8662
0.9171
MATLAB places the points at unequal step sizes of time. This is what their documentation has to say:
|
Let's take a look at the Python output: >>> t[0:10]
array([[ 0. ],
[ 0.1],
[ 0.2],
[ 0.3],
[ 0.4],
[ 0.5],
[ 0.6],
[ 0.7],
[ 0.8],
[ 0.9]])
>>> CA[0:10]
array([[ 0.5 ],
[ 0.53581076],
[ 0.57035065],
[ 0.60362937],
[ 0.63566104],
[ 0.66646269],
[ 0.69605419],
[ 0.7244578 ],
[ 0.75169755],
[ 0.77779875]]
The evenly spaced periods of time were by design - see the Python code above. After reading the MATLAB description alongside, you might think the Python integration is inaccurate. This is not true: the Python code we have used here will take multiple steps, of variable size, within each of the delta_t time steps we specified, but the code will only report the values at the boundaries of each delta_t, not the intermediate values. |
Example with coupled ODEs
We will now expand our example to a system of two coupled ODEs. Still in the same reactor we are now considering the rate constant to be a function of temperature: \(k = 0.15 e^{- E_a/(RT)}\) L/(mol.min), with \(E_a = 5000\) J/(mol) and R = \(8.314 \) J/mol.K, and \(T(t)\) is the time-varying tank temperature, measured in Kelvin. Furthermore, the reaction is known to release heat, with \(\Delta H_r = -590\) J/mol. The time-dependent mass and energy balance for this system is now:
\[ \begin{align*}\frac{dC_{\sf A}(t)}{dt} &= \frac{F(t)}{V} \bigg( C_{{\sf A},\text{in}} - C_{\sf A} \bigg) - 0.15 e^{- E_a/(RT)} C_{\sf A}^2 \\ \frac{dT(t)}{dt} &= \frac{F(t)\rho C_p(T)}{V \rho C_p(T)}\bigg(T_\text{in} - T(t) \bigg) - \frac{0.15 e^{- E_a/(RT)} C_{\sf A}^2 V (\Delta H_r)}{V \rho C_p}\end{align*}\]
where \(C_{{\sf A},\text{in}} = 2.5\) mol/L, \(T_\text{in} = 288\) K; we will initially assume constant volume of \(V = 100\) L and constant inlet flow of \(F(t) = 20.1 \) L/min. Also, \(C_p(T) = 4.184 - 0.002(T-273) \) J/(kg.K), the molar heat capacity of the liquid phase system, a weak function of the system temperature. The density of the liquid phase is \(\rho=1.05\) kg/L. We need two initial conditions as well:
- \( C_{\sf A}(t=0) = 0.5\) mol/L
- \(T(t=0) = 295 K \)
In the code below we will integrate the ODE from \(t_\text{start} = 0.0\) minutes up to \(t_\text{final} = 45.0\) minutes and plot the time-varying trajectory of concentration in the tank.
- Important notes
- Each trajectory (ODE) must have an initial condition.
- The function that specifies the ODE must return a column vector with \(n\) entries, one for each ODE.
- Algebraic equations may be included in the ODE function. For example:
- \(C_p = 4.184 - 0.002(T-273)\) is an algebraic function
- If the inlet flow varied over time according to \(F(t) = 20.1 + 2\sin(t)\) then this algebraic equation could be added.
- Numerical integration allows for discontinuities. For example, a step input at \(t=50\) minutes in the inlet flow can be coded as
if t < 50
F = 20.1
else
F = 25.1
end