Difference between revisions of "Principal Component Analysis"
Jump to navigation
Jump to search
Kevin Dunn (talk | contribs) |
Kevin Dunn (talk | contribs) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 43: | Line 43: | ||
== Class 2 (16 September 2011) == | == Class 2 (16 September 2011) == | ||
[[Media:Lvm-class-2.pdf|Download the class slides]] | |||
[[Image:Nuvola_mimetypes_pdf.png|20px|link=Media:Lvm-class-2.pdf]] [[Media:Lvm-class-2.pdf|Download the class slides]] (PDF) | |||
| Line 72: | Line 73: | ||
== Class 3 == | == Class 3 (23, 30 September 2011) == | ||
[[Media:Lvm-class-3.pdf|Download the class slides]] | [[Image:Nuvola_mimetypes_pdf.png|20px|link=Media:Lvm-class-3.pdf]] [[Media:Lvm-class-3.pdf|Download the class slides]] (PDF) | ||
Latest revision as of 14:04, 17 September 2018
| Class date(s): | 16, 23, 30 September 2011 | ||||
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
Class 2 (16 September 2011)
![]() Download the class slides (PDF)
Download the class slides (PDF)
- Download these 3 CSV files and bring them on your computer:
- Peas dataset: http://openmv.net/info/peas
- Food texture dataset: http://openmv.net/info/food-texture
- Food consumption dataset: http://openmv.net/info/food-consumption
Background reading
- Reading for class 2
- Linear algebra topics you should be familiar with before class 2:
- matrix multiplication
- that matrix multiplication of a vector by a matrix is a transformation from one coordinate system to another (we will review this in class)
- linear combinations (read the first section of that website: we will review this in class)
- the dot product of 2 vectors, and that they are related by the cosine of the angle between them (see the geometric interpretation section)
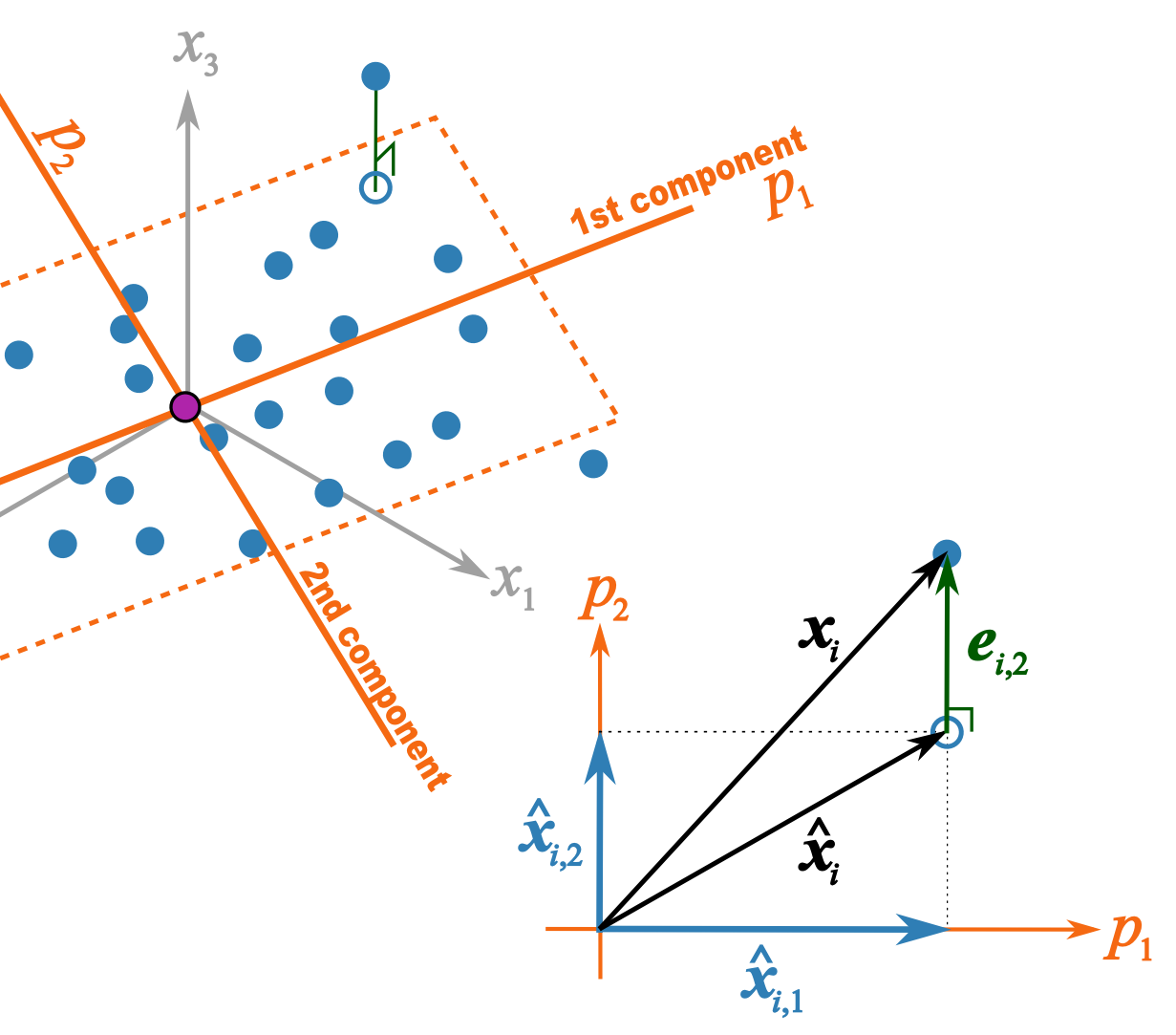
This illustration should help better explain what I trying to get across in class 2B
- \(p_1\) and \(p_2\) are the unit vectors for components 1 and 2.
- \( \mathbf{x}_i \) is a row of data from matrix \( \mathbf{X}\).
- \(\hat{\mathbf{x}}_{i,1} = t_{i,1}p_1\) = the best prediction of \( \mathbf{x}_i \) using only the first component.
- \(\hat{\mathbf{x}}_{i,2} = t_{i,2}p_2\) = the improvement we add after the first component to better predict \( \mathbf{x}_i \).
- \(\hat{\mathbf{x}}_{i} = \hat{\mathbf{x}}_{i,1} + \hat{\mathbf{x}}_{i,2} \) = is the total prediction of \( \mathbf{x}_i \) using 2 components and is the open blue point lying on the plane defined by \(p_1\) and \(p_2\). Notice that this is just the vector summation of \( \hat{\mathbf{x}}_{i,1}\) and \( \hat{\mathbf{x}}_{i,2}\).
- \(\mathbf{e}_{i,2} \) = is the prediction error vector because the prediction \(\hat{\mathbf{x}}_{i} \) is not exact: the data point \( \mathbf{x}_i \) lies above the plane defined by \(p_1\) and \(p_2\). This \(e_{i,2} \) is the residual distance after using 2 components.
- \( \mathbf{x}_i = \hat{\mathbf{x}}_{i} + \mathbf{e}_{i,2} \) is also a vector summation and shows how \( \mathbf{x}_i \) is broken down into two parts: \(\hat{\mathbf{x}}_{i} \) is a vector on the plane, while \( \mathbf{e}_{i,2} \) is the vector perpendicular to the plane.
Class 3 (23, 30 September 2011)
![]() Download the class slides (PDF)
Download the class slides (PDF)
Background reading
- Least squares:
- what is the objective function of least squares
- how to calculate the regression coefficient \(b\) for \(y = bx + e\) where \(x\) and \(y\) are centered vectors
- understand that the residuals in least squares are orthogonal to \(x\)
- Some optimization theory:
- How an optimization problem is written with equality constraints
- The Lagrange multiplier principle for solving simple, equality constrained optimization problems.
Background reading
- Reading on cross validation