Difference between revisions of "Principal Component Analysis"
Jump to navigation
Jump to search
Kevin Dunn (talk | contribs) m |
Kevin Dunn (talk | contribs) |
||
| (30 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{ | {{ClassSidebarYouTube | ||
| date = | | date = 16, 23, 30 September 2011 | ||
| | | vimeoID1 = 9QzNOz_7i6U | ||
| | | vimeoID2 = qDiPZp-FWc4 | ||
| | | vimeoID3 = y0Alf0VZ-1E | ||
| | | vimeoID4 = XfH_p1WAydM | ||
| vimeoID5 = QLB-UJ1dFiE | |||
| vimeoID6 = bysqF41Mgc0 | |||
| vimeoID7 = p3i-XsviARM | |||
| vimeoID8 = Qb28yc3eM0Q | |||
| vimeoID9 = | |||
| course_notes_PDF = | | course_notes_PDF = | ||
| course_notes_alt = Course notes | | course_notes_alt = Course notes | ||
| overheads_PDF = | | overheads_PDF = | ||
| assignment_instructions = | | overheads_PDF_alt = Projector notes | ||
| | | assignment_instructions = | ||
| | | assignment_solutions = | ||
| | | video_download_link_MP4 = http://learnche.mcmaster.ca/media/LVM-2011-Class-02A.mp4 | ||
| | | video_download_link2_MP4 = http://learnche.mcmaster.ca/media/LVM-2011-Class-02B.mp4 | ||
| | | video_download_link3_MP4 = http://learnche.mcmaster.ca/media/LVM-2011-Class-02C.mp4 | ||
| | | video_download_link4_MP4 = http://learnche.mcmaster.ca/media/LVM-2011-Class-03A.mp4 | ||
| video_download_link3_MP4_size = Mb | | video_download_link5_MP4 = http://learnche.mcmaster.ca/media/LVM-2011-Class-03B.mp4 | ||
| video_download_link6_MP4 = http://learnche.mcmaster.ca/media/LVM-2011-Class-03C.mp4 | |||
| video_download_link7_MP4 = http://learnche.mcmaster.ca/media/LVM-2011-Class-04A.mp4 | |||
| video_download_link8_MP4 = http://learnche.mcmaster.ca/media/LVM-2011-Class-04B.mp4 | |||
| video_download_link9_MP4 = | |||
| video_download_link_MP4_size = 290 Mb | |||
| video_download_link2_MP4_size = 306 Mb | |||
| video_download_link3_MP4_size = 294 Mb | |||
| video_download_link4_MP4_size = 152 Mb | |||
| video_download_link5_MP4_size = 276 Mb | |||
| video_download_link6_MP4_size = 333 Mb | |||
| video_download_link7_MP4_size = 198 Mb | |||
| video_download_link8_MP4_size = 180 Mb | |||
| video_download_link9_MP4_size = Mb | |||
| video_notes1 = | | video_notes1 = | ||
| video_notes2 = | | video_notes2 = | ||
| video_notes3 = | |||
| video_notes4 = | |||
| video_notes5 = | |||
| video_notes6 = | |||
}}__NOTOC__ | |||
== Class 2 (16 September 2011) == | |||
[[Image:Nuvola_mimetypes_pdf.png|20px|link=Media:Lvm-class-2.pdf]] [[Media:Lvm-class-2.pdf|Download the class slides]] (PDF) | |||
== | * Download these 3 CSV files and bring them on your computer: | ||
** Peas dataset: http://openmv.net/info/peas | |||
** Food texture dataset: http://openmv.net/info/food-texture | |||
** Food consumption dataset: http://openmv.net/info/food-consumption | |||
=== Background reading === | |||
* [http://literature.connectmv.com/item/13/principal-component-analysis Reading for class 2] | * [http://literature.connectmv.com/item/13/principal-component-analysis Reading for class 2] | ||
* Linear algebra topics you should be familiar with before class 2: | * Linear algebra topics you should be familiar with before class 2: | ||
** matrix multiplication | ** matrix multiplication | ||
** that matrix multiplication of a vector by a matrix is a transformation from one coordinate system to another (we will review this in class) | ** that matrix multiplication of a vector by a matrix is a transformation from one coordinate system to another (we will review this in class) | ||
** [ | ** [https://en.wikipedia.org/wiki/Linear_combination linear combinations] (read the first section of that website: we will review this in class) | ||
** the dot product of 2 vectors, and that they are related by the cosine of the angle between them (see the [http://en.wikipedia.org/wiki/Dot_product geometric interpretation section]) | ** the dot product of 2 vectors, and that they are related by the cosine of the angle between them (see the [http://en.wikipedia.org/wiki/Dot_product geometric interpretation section]) | ||
This illustration should help better explain what I trying to get across in class 2B | This illustration should help better explain what I trying to get across in class 2B | ||
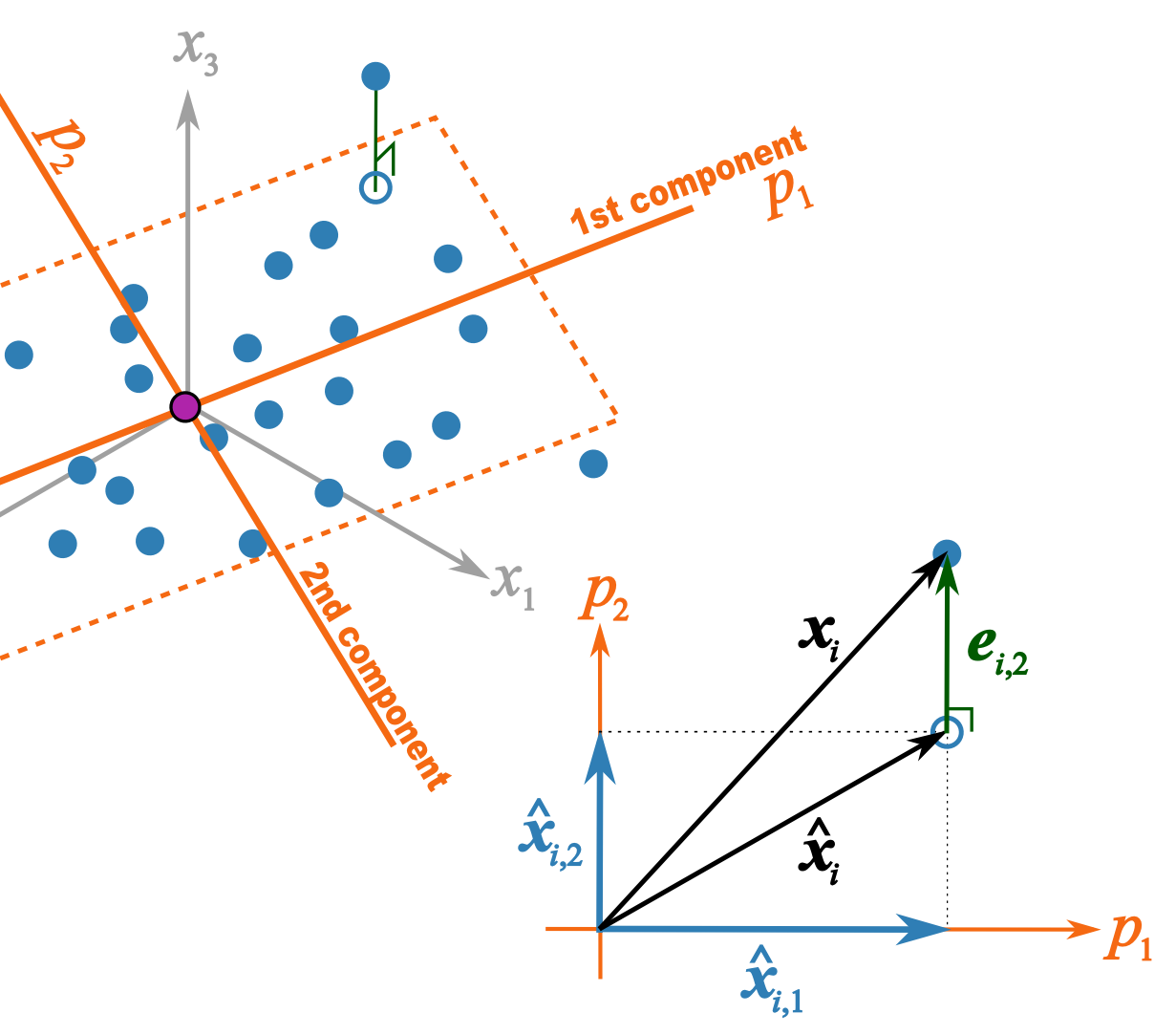
* \(p_1\) and \(p_2\) are the unit vectors for components 1 and 2. | * \(p_1\) and \(p_2\) are the unit vectors for components 1 and 2. | ||
* \( \mathbf{x}_i \) is a row of data from matrix \( \mathbf{X}\). | * \( \mathbf{x}_i \) is a row of data from matrix \( \mathbf{X}\). | ||
| Line 87: | Line 70: | ||
* \(\mathbf{e}_{i,2} \) = is the prediction error '''''vector''''' because the prediction \(\hat{\mathbf{x}}_{i} \) is not exact: the data point \( \mathbf{x}_i \) lies above the plane defined by \(p_1\) and \(p_2\). This \(e_{i,2} \) is the residual distance after using 2 components. | * \(\mathbf{e}_{i,2} \) = is the prediction error '''''vector''''' because the prediction \(\hat{\mathbf{x}}_{i} \) is not exact: the data point \( \mathbf{x}_i \) lies above the plane defined by \(p_1\) and \(p_2\). This \(e_{i,2} \) is the residual distance after using 2 components. | ||
* \( \mathbf{x}_i = \hat{\mathbf{x}}_{i} + \mathbf{e}_{i,2} \) is also a vector summation and shows how \( \mathbf{x}_i \) is broken down into two parts: \(\hat{\mathbf{x}}_{i} \) is a vector on the plane, while \( \mathbf{e}_{i,2} \) is the vector perpendicular to the plane. | * \( \mathbf{x}_i = \hat{\mathbf{x}}_{i} + \mathbf{e}_{i,2} \) is also a vector summation and shows how \( \mathbf{x}_i \) is broken down into two parts: \(\hat{\mathbf{x}}_{i} \) is a vector on the plane, while \( \mathbf{e}_{i,2} \) is the vector perpendicular to the plane. | ||
| | [[Image:geometric-interpretation-of-PCA-xhat-residuals.png|500px]] | ||
== Class 3 (23, 30 September 2011) == | |||
[[Image:Nuvola_mimetypes_pdf.png|20px|link=Media:Lvm-class-3.pdf]] [[Media:Lvm-class-3.pdf|Download the class slides]] (PDF) | |||
===Background reading === | |||
* Least squares: | |||
** what is the objective function of least squares | |||
** how to calculate the regression coefficient \(b\) for \(y = bx + e\) where \(x\) and \(y\) are centered vectors | |||
** understand that the residuals in least squares are orthogonal to \(x\) | |||
* Some optimization theory: | |||
** How an optimization problem is written with equality constraints | |||
** The [https://en.wikipedia.org/wiki/Lagrange_multiplier Lagrange multiplier principle] for solving simple, equality constrained optimization problems. | |||
===Background reading === | |||
* Reading on [http://literature.connectmv.com/item/12/cross-validatory-estimation-of-the-number-of-components-in-factor-and-principal-components-models cross validation] | |||
Latest revision as of 14:04, 17 September 2018
| Class date(s): | 16, 23, 30 September 2011 | ||||
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
Class 2 (16 September 2011)
![]() Download the class slides (PDF)
Download the class slides (PDF)
- Download these 3 CSV files and bring them on your computer:
- Peas dataset: http://openmv.net/info/peas
- Food texture dataset: http://openmv.net/info/food-texture
- Food consumption dataset: http://openmv.net/info/food-consumption
Background reading
- Reading for class 2
- Linear algebra topics you should be familiar with before class 2:
- matrix multiplication
- that matrix multiplication of a vector by a matrix is a transformation from one coordinate system to another (we will review this in class)
- linear combinations (read the first section of that website: we will review this in class)
- the dot product of 2 vectors, and that they are related by the cosine of the angle between them (see the geometric interpretation section)
This illustration should help better explain what I trying to get across in class 2B
- \(p_1\) and \(p_2\) are the unit vectors for components 1 and 2.
- \( \mathbf{x}_i \) is a row of data from matrix \( \mathbf{X}\).
- \(\hat{\mathbf{x}}_{i,1} = t_{i,1}p_1\) = the best prediction of \( \mathbf{x}_i \) using only the first component.
- \(\hat{\mathbf{x}}_{i,2} = t_{i,2}p_2\) = the improvement we add after the first component to better predict \( \mathbf{x}_i \).
- \(\hat{\mathbf{x}}_{i} = \hat{\mathbf{x}}_{i,1} + \hat{\mathbf{x}}_{i,2} \) = is the total prediction of \( \mathbf{x}_i \) using 2 components and is the open blue point lying on the plane defined by \(p_1\) and \(p_2\). Notice that this is just the vector summation of \( \hat{\mathbf{x}}_{i,1}\) and \( \hat{\mathbf{x}}_{i,2}\).
- \(\mathbf{e}_{i,2} \) = is the prediction error vector because the prediction \(\hat{\mathbf{x}}_{i} \) is not exact: the data point \( \mathbf{x}_i \) lies above the plane defined by \(p_1\) and \(p_2\). This \(e_{i,2} \) is the residual distance after using 2 components.
- \( \mathbf{x}_i = \hat{\mathbf{x}}_{i} + \mathbf{e}_{i,2} \) is also a vector summation and shows how \( \mathbf{x}_i \) is broken down into two parts: \(\hat{\mathbf{x}}_{i} \) is a vector on the plane, while \( \mathbf{e}_{i,2} \) is the vector perpendicular to the plane.
Class 3 (23, 30 September 2011)
![]() Download the class slides (PDF)
Download the class slides (PDF)
Background reading
- Least squares:
- what is the objective function of least squares
- how to calculate the regression coefficient \(b\) for \(y = bx + e\) where \(x\) and \(y\) are centered vectors
- understand that the residuals in least squares are orthogonal to \(x\)
- Some optimization theory:
- How an optimization problem is written with equality constraints
- The Lagrange multiplier principle for solving simple, equality constrained optimization problems.
Background reading
- Reading on cross validation