| Class date(s):
|
16, 23, 30 September 2011
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Class 2
<pdfreflow>
class_date = 16 September 2011 [1.65 Mb]
button_label = Create my projector slides!
show_page_layout = 1
show_frame_option = 1
pdf_file = lvm-class-2.pdf
</pdfreflow>
or you may download the class slides directly.
- Download these 3 CSV files and bring them on your computer:
Background reading
- Reading for class 2
- Linear algebra topics you should be familiar with before class 2:
- matrix multiplication
- that matrix multiplication of a vector by a matrix is a transformation from one coordinate system to another (we will review this in class)
- linear combinations (read the first section of that website: we will review this in class)
- the dot product of 2 vectors, and that they are related by the cosine of the angle between them (see the geometric interpretation section)
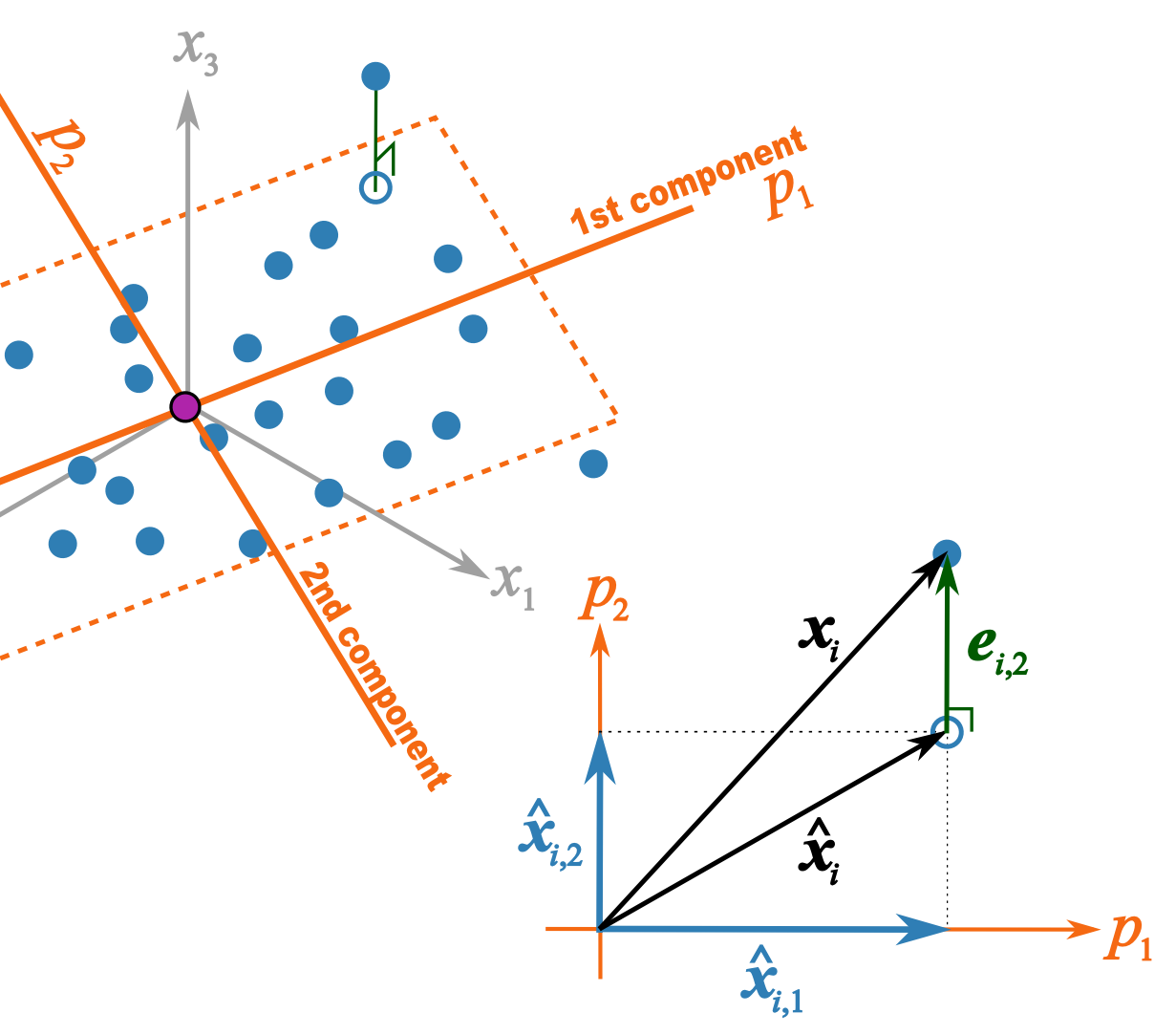
This illustration should help better explain what I trying to get across in class 2B
- and are the unit vectors for components 1 and 2.
- is a row of data from matrix .
- = the best prediction of using only the first component.
- = the improvement we add after the first component to better predict .
- = is the total prediction of using 2 components and is the open blue point lying on the plane defined by and . Notice that this is just the vector summation of and .
- = is the prediction error vector because the prediction is not exact: the data point lies above the plane defined by and . This is the residual distance after using 2 components.
- is also a vector summation and shows how is broken down into two parts: is a vector on the plane, while is the vector perpendicular to the plane.
Class 3
<pdfreflow>
class_date = 23, 30 September 2011 [580 Kb]
button_label = Create my projector slides!
show_page_layout = 1
show_frame_option = 1
pdf_file = lvm-class-3.pdf
</pdfreflow>
or you may download the class slides directly.
Background reading
- Least squares:
- what is the objective function of least squares
- how to calculate the regression coefficient for where and are centered vectors
- understand that the residuals in least squares are orthogonal to
- Some optimization theory:
- How an optimization problem is written with equality constraints
- The Lagrange multiplier principle for solving simple, equality constrained optimization problems.
Background reading
