Difference between revisions of "Isothermal reactor design - 2013"
Kevin Dunn (talk | contribs) |
Kevin Dunn (talk | contribs) |
||
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{ | {{ClassSidebarYouTube | ||
| date = 04 February to | | date = 04 February to 27 February | ||
| dates_alt_text = | | dates_alt_text = | ||
| vimeoID1 = | | vimeoID1 = liXKOzGkkAM | ||
| vimeoID2 = | | vimeoID2 = yOuoJWCLHf8 | ||
| vimeoID3 = | | vimeoID3 = A2NwDXMAnm0 | ||
| vimeoID4 = | | vimeoID4 = _PJIQthv9DI | ||
| vimeoID5 = | | vimeoID5 = g3lo65jTTE4 | ||
| vimeoID6 = dGVttCtyJXY | |||
| vimeoID7 = AC7u8_56MnI | |||
| course_notes_PDF = | | course_notes_PDF = | ||
| course_notes_alt = Course notes | | course_notes_alt = Course notes | ||
| Line 27: | Line 29: | ||
| video_download_link5_MP4_size = 243 M | | video_download_link5_MP4_size = 243 M | ||
| video_notes5 = | | video_notes5 = | ||
| video_download_link6_MP4 = http://learnche.mcmaster.ca/media/3K4-2013-Class-07A.mp4 | |||
| video_download_link6_MP4_size = 353 M | |||
| video_notes6 = | |||
| video_download_link7_MP4 = http://learnche.mcmaster.ca/media/3K4-2013-Class-07B.mp4 | |||
| video_download_link7_MP4_size = 240 M | |||
| video_notes7 = | |||
}}__NOTOC__ | }}__NOTOC__ | ||
| Line 62: | Line 70: | ||
* [http://learnche.mcmaster.ca/media/3K4-2013-Class-06C.mp3 Audio] and [http://learnche.mcmaster.ca/media/3K4-2013-Class-06C.mp4 video] recording of the class | * [http://learnche.mcmaster.ca/media/3K4-2013-Class-06C.mp3 Audio] and [http://learnche.mcmaster.ca/media/3K4-2013-Class-06C.mp4 video] recording of the class | ||
=== 25 February 2013 (07A) === | === 25 and 27 February 2013 (07A and 07B) === | ||
* [http://learnche.mcmaster.ca/media/3K4-2013-Class-07A.mp3 Audio] and [http://learnche.mcmaster.ca/media/3K4-2013-Class-07A.mp4 video] recording of | * [http://learnche.mcmaster.ca/media/3K4-2013-Class-07A.mp3 Audio] and [http://learnche.mcmaster.ca/media/3K4-2013-Class-07A.mp4 video] recording of class 07A | ||
* [http://learnche.mcmaster.ca/media/3K4-2013-Class-07B.mp3 Audio] and [http://learnche.mcmaster.ca/media/3K4-2013-Class-07B.mp4 video] recording of class 07B | |||
The example covered in class is based on example 4-8 in F2006 and example 6-2 in F2011. | The example covered in class is based on example 4-8 in F2006 and example 6-2 in F2011. | ||
<rst> | <rst> | ||
<rst-options: 'toc' = False/> | |||
<rst-options: 'reset-figures' = False/> | |||
The 3 ODE's are: | The 3 ODE's are: | ||
| Line 90: | Line 101: | ||
C_A = C_\text{T0}\left(\dfrac{F_A}{F_T}\right) | C_A = C_\text{T0}\left(\dfrac{F_A}{F_T}\right) | ||
where :math:`F_T = F_A + F_B + F_C` and :math:`C_\text{T0} = \dfrac{P_0}{RT_0}` | where :math:`F_T = F_A + F_B + F_C` and :math:`C_\text{T0} = \dfrac{P_0}{RT_0}`. Similar equations can be written for :math:`C_B` and :math:`C_C`. | ||
Using all of the above derivations, we can set up our numerical integration as shown below. | Using all of the above derivations, we can set up our numerical integration as shown below. | ||
</rst> | </rst> | ||
=== MATLAB === | |||
In a file called '''<tt>membrane.m</tt>''': | In a file called '''<tt>membrane.m</tt>''': | ||
<syntaxhighlight lang="matlab"> | <syntaxhighlight lang="matlab"> | ||
function d_depnt__d_indep = membranem(indep, depnt) | |||
% Dynamic balance for the packed bed reactor (PBR); demo problem class 05C | |||
% | |||
% indep: the independent ODE variable, such as time or length | |||
% depnt: a vector of dependent variables | |||
% | |||
% X = depnt(1) = the conversion | |||
% y = depnt(2) = the pressure ratio = P/P_0 = y | |||
% | |||
% Returns d(depnt)/d(indep) = a vector of ODEs | |||
% Assign some variables for convenience of notation | |||
FA = depnt(1); | |||
FB = depnt(2); | |||
FC = depnt(3); | |||
% Constants | |||
kDiff = 0.005; % s^{-1} | |||
k = 0.01; % s^{-1} | |||
KC = 50; % mol.m^{-3} | |||
P0 = 830600; % Pa | |||
T0 = 500; % K | |||
R = 8.314; % J/(mol.K) | |||
% Algebraic equations | |||
FT = FA + FB + FC; | |||
CT0 = P0 / (R * T0); | |||
CA = CT0 * FA / FT; | |||
CB = CT0 * FB / FT; | |||
CC = CT0 * FC / FT; | |||
RB = kDiff * CB; | |||
rA = -k * (CA - CB * CC / KC); | |||
rB = -rA; | |||
rC = -rA; | |||
% Output from this ODE function must be a COLUMN vector, with n rows | |||
n = numel(depnt); | |||
d_depnt__d_indep = zeros(n,1); | |||
d_depnt__d_indep(1) = rA; | |||
d_depnt__d_indep(2) = rB - RB; | |||
d_depnt__d_indep(3) = rC; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
In a separate file (any name), for example: '''<tt>ode_driver.m</tt>''', which will "drive" the ODE solver: | In a separate file (any name), for example: '''<tt>ode_driver.m</tt>''', which will "drive" the ODE solver: | ||
<syntaxhighlight lang="matlab"> | <syntaxhighlight lang="matlab"> | ||
% Integrate the ODE | |||
% ----------------- | |||
% The independent variable always requires an initial and final value: | |||
indep_start = 0.0; % m^3 | |||
indep_final = 0.4; % m^3 | |||
% Set initial condition(s): for integrating variables (dependent variables) | |||
FA_depnt_zero = 0.25; % i.e. FA(V=0) = 15 mol/min = 0.25 mol/s | |||
FB_depnt_zero = 0.0; % i.e. FB(V=0) = 0 mol/s | |||
FC_depnt_zero = 0.0; % i.e. FC(V=0) = 0 mol/s | |||
% Integrate the ODE(s): | |||
[V, depnt] = ode45(@membranem, [indep_start, indep_final], [FA_depnt_zero, FB_depnt_zero, FC_depnt_zero]); | |||
% Plot the results: | |||
clf; | |||
plot(V, depnt(:,1), 'b') | |||
grid('on') | |||
hold('on') | |||
plot(V, depnt(:,2), 'g') | |||
plot(V, depnt(:,3), 'r') | |||
xlabel('Reactor volume, V [m^3]') | |||
ylabel('F_A, F_B and F_C') | |||
legend('F_A', 'F_B', 'F_C') | |||
</syntaxhighlight> | </syntaxhighlight> | ||
[[Image: | [[Image:MATLAB-07A-example.png | 550px]] | ||
=== Python === | |||
<syntaxhighlight lang="python"> | <syntaxhighlight lang="python"> | ||
import numpy as np | |||
from scipy import integrate | |||
from matplotlib.pylab import (plot, grid, xlabel, ylabel, show, legend) | |||
def membrane(indep, depnt): | |||
""" | |||
Dynamic balance for the membrane reactor; class 07A | |||
indep: the independent ODE variable, such as time or length | |||
depnt: a vector of dependent variables | |||
X = depnt[0] = the conversion | |||
y = depnt[1] = the pressure ratio = P/P_0 = y | |||
Returns d(depnt)/d(indep) = a vector of ODEs | |||
""" | |||
# Assign some variables for convenience of notation | |||
FA = depnt[0] | |||
FB = depnt[1] | |||
FC = depnt[2] | |||
# Constants | |||
kDiff = 0.005 # s^{-1} | |||
k = 0.01 # s^{-1} | |||
KC = 50 # mol.m^{-3} | |||
P0 = 830600 # Pa | |||
T0 = 500 # K | |||
R = 8.314 # J/(mol.K) | |||
# Algebraic equations | |||
FT = FA + FB + FC | |||
CT0 = P0 / (R * T0) | |||
CA = CT0 * FA / FT | |||
CB = CT0 * FB / FT | |||
CC = CT0 * FC / FT | |||
R_B = kDiff * CB | |||
rA = -k * (CA - CB * CC / KC) | |||
rB = -rA | |||
rC = -rA | |||
# Output from this ODE function must be a COLUMN vector, with n rows | |||
n = len(depnt) | |||
d_depnt__d_indep = np.zeros((n,1)) | |||
d_depnt__d_indep[0] = rA | |||
d_depnt__d_indep[1] = rB - R_B | |||
d_depnt__d_indep[2] = rC | |||
return d_depnt__d_indep | |||
# The "driver" that will integrate the ODE(s): | |||
# ----------- | |||
# Start by specifying the integrator: | |||
# use ``vode`` with "backward differentiation formula" | |||
r = integrate.ode(membrane).set_integrator('vode', method='bdf') | |||
# Set the independent variable's range | |||
indep_start = 0.0 # m^3 | |||
indep_final = 0.4 # m^3 | |||
delta = 0.01 # the results will be shown only at these ``delta`` points | |||
num_steps = np.floor((indep_final - indep_start)/delta) + 1 # Number of steps: 1 extra for initial condition | |||
# Set initial condition(s): for integrating variables (dependent variables) | |||
FA_depnt_zero = 0.25 # i.e. FA(V=0) = 15 mol/min = 0.25 mol/s | |||
FB_depnt_zero = 0.0 # i.e. FB(V=0) = 0 mol/s | |||
FC_depnt_zero = 0.0 # i.e. FC(V=0) = 0 mol/s | |||
r.set_initial_value([FA_depnt_zero, FB_depnt_zero, FC_depnt_zero], indep_start) | |||
# Create vectors to store trajectories | |||
V = np.zeros((num_steps, 1)) | |||
FA = np.zeros((num_steps, 1)) | |||
FB = np.zeros((num_steps, 1)) | |||
FC = np.zeros((num_steps, 1)) | |||
V[0] = indep_start | |||
FA[0] = FA_depnt_zero | |||
FB[0] = FB_depnt_zero | |||
FC[0] = FC_depnt_zero | |||
# Integrate the ODE(s) across each delta | |||
k = 1 | |||
while r.successful() and k < num_steps: | |||
r.integrate(r.t + delta) | |||
# Store the results to plot later | |||
V[k] = r.t | |||
FA[k] = r.y[0] | |||
FB[k] = r.y[1] | |||
FC[k] = r.y[2] | |||
k += 1 | |||
# All done! Plot the trajectories: | |||
plot(V, FA) | |||
grid('on') | |||
plot(V, FB) | |||
plot(V, FC) | |||
xlabel('Volume, $V$ [$m^3$]') | |||
ylabel('$F_A, F_B, F_C$ [mol/s]') | |||
legend(['$F_A$', '$F_B$', '$F_C$']) | |||
show() | |||
</syntaxhighlight> | </syntaxhighlight> | ||
[[Image: | [[Image:Python-07A-example.png|850px]] | ||
=== Polymath === | |||
<syntaxhighlight lang="text"> | <syntaxhighlight lang="text"> | ||
d(FA)/d(V) = rA | d(FA)/d(V) = rA | ||
d(FB)/d(V) = rB - | d(FB)/d(V) = rB - RB | ||
d(FC)/d(V) = rC | d(FC)/d(V) = rC | ||
| Line 131: | Line 300: | ||
V(0) = 0 | V(0) = 0 | ||
V(f) = 0.4 #m^3 | V(f) = 0.4 #m^3 | ||
# Constants | # Constants | ||
| Line 149: | Line 308: | ||
T0 = 500 # K | T0 = 500 # K | ||
R = 8.314 # J/(mol.K) | R = 8.314 # J/(mol.K) | ||
# Algebraic equations | |||
FT = FA + FB + FC | |||
CT0 = P0 / (R * T0) | |||
CA = CT0 * FA / FT | |||
CB = CT0 * FB / FT | |||
CC = CT0 * FC / FT | |||
RB = kDiff * CB | |||
rA = -k * (CA - CB * CC / KC) | |||
rB = -rA | |||
rC = -rA | |||
</syntaxhighlight> | </syntaxhighlight> | ||
Latest revision as of 19:23, 6 January 2017
| Class date(s): | 04 February to 27 February | ||||
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
| |||||
- F2011: Chapter 5 and 6
- F2006: Chapter 4
04 February 2013 (05A)
- General problem solving strategy for reactor engineering
- Audio and video recording of the class
06 February 2013 (05B)
- The Ergun equation derivation
- Audio and video recording of the class
07 February 2013 (05C)
- Notes used during the class
- The spreadsheet with the Ergun equation example. Use it to try
- different lengths of reactor
- different catalyst particle sizes
- different pipe diameters
- gas properties (e.g. density)
- to see the effect on pressure drop in the packed bed.
11 February 2013 (06A)
- Audio and video recording of the class
- Codes to solve the example in class are available on the page software for integrating ODEs.
14 February 2013 (06C): midterm review
25 and 27 February 2013 (07A and 07B)
The example covered in class is based on example 4-8 in F2006 and example 6-2 in F2011. <rst> <rst-options: 'toc' = False/> <rst-options: 'reset-figures' = False/> The 3 ODE's are:
.. math::
\dfrac{dF_A}{dV} &= r_A\\ \dfrac{dF_B}{dV} &= r_B - R_B \\ \dfrac{dF_C}{dV} &= r_C
where :math:`-r_A = r_B = r_C` and :math:`-r_A = k\left(C_A - \dfrac{C_B C_C}{K_C} \right)`, and :math:`R_B = k_\text{diff}C_B`.
- :math:`k = 0.01\,\text{s}^{-1}`
- :math:`k_\text{diff} = 0.005\,\text{s}^{-1}`
- :math:`K_C = 50\,\text{mol.m}^{-3}`
We derived earlier in the course that
.. math:: C_A = C_\text{TO}\left(\dfrac{F_A}{F_T}\right)\left(\dfrac{P}{P_0}\right)\left(\dfrac{T_0}{T}\right)
Assuming isothermal and isobaric conditions in the membrane:
.. math:: C_A = C_\text{T0}\left(\dfrac{F_A}{F_T}\right)
where :math:`F_T = F_A + F_B + F_C` and :math:`C_\text{T0} = \dfrac{P_0}{RT_0}`. Similar equations can be written for :math:`C_B` and :math:`C_C`.
Using all of the above derivations, we can set up our numerical integration as shown below. </rst>
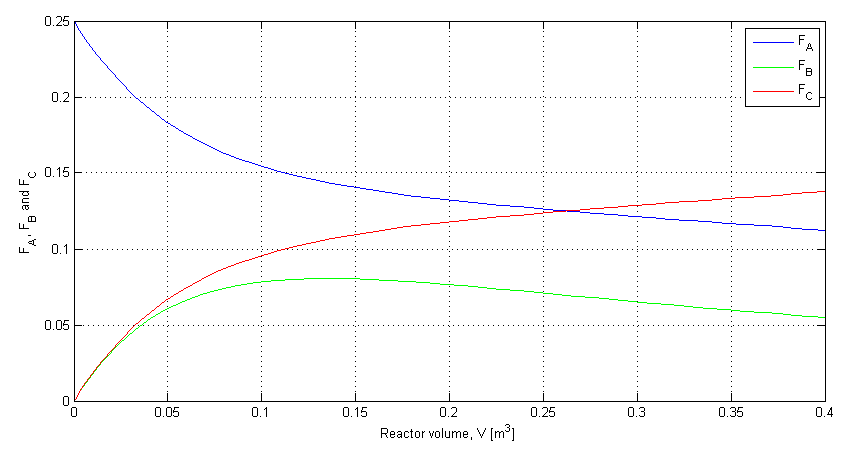
MATLAB
In a file called membrane.m:
function d_depnt__d_indep = membranem(indep, depnt)
% Dynamic balance for the packed bed reactor (PBR); demo problem class 05C
%
% indep: the independent ODE variable, such as time or length
% depnt: a vector of dependent variables
%
% X = depnt(1) = the conversion
% y = depnt(2) = the pressure ratio = P/P_0 = y
%
% Returns d(depnt)/d(indep) = a vector of ODEs
% Assign some variables for convenience of notation
FA = depnt(1);
FB = depnt(2);
FC = depnt(3);
% Constants
kDiff = 0.005; % s^{-1}
k = 0.01; % s^{-1}
KC = 50; % mol.m^{-3}
P0 = 830600; % Pa
T0 = 500; % K
R = 8.314; % J/(mol.K)
% Algebraic equations
FT = FA + FB + FC;
CT0 = P0 / (R * T0);
CA = CT0 * FA / FT;
CB = CT0 * FB / FT;
CC = CT0 * FC / FT;
RB = kDiff * CB;
rA = -k * (CA - CB * CC / KC);
rB = -rA;
rC = -rA;
% Output from this ODE function must be a COLUMN vector, with n rows
n = numel(depnt);
d_depnt__d_indep = zeros(n,1);
d_depnt__d_indep(1) = rA;
d_depnt__d_indep(2) = rB - RB;
d_depnt__d_indep(3) = rC;
In a separate file (any name), for example: ode_driver.m, which will "drive" the ODE solver:
% Integrate the ODE
% -----------------
% The independent variable always requires an initial and final value:
indep_start = 0.0; % m^3
indep_final = 0.4; % m^3
% Set initial condition(s): for integrating variables (dependent variables)
FA_depnt_zero = 0.25; % i.e. FA(V=0) = 15 mol/min = 0.25 mol/s
FB_depnt_zero = 0.0; % i.e. FB(V=0) = 0 mol/s
FC_depnt_zero = 0.0; % i.e. FC(V=0) = 0 mol/s
% Integrate the ODE(s):
[V, depnt] = ode45(@membranem, [indep_start, indep_final], [FA_depnt_zero, FB_depnt_zero, FC_depnt_zero]);
% Plot the results:
clf;
plot(V, depnt(:,1), 'b')
grid('on')
hold('on')
plot(V, depnt(:,2), 'g')
plot(V, depnt(:,3), 'r')
xlabel('Reactor volume, V [m^3]')
ylabel('F_A, F_B and F_C')
legend('F_A', 'F_B', 'F_C')
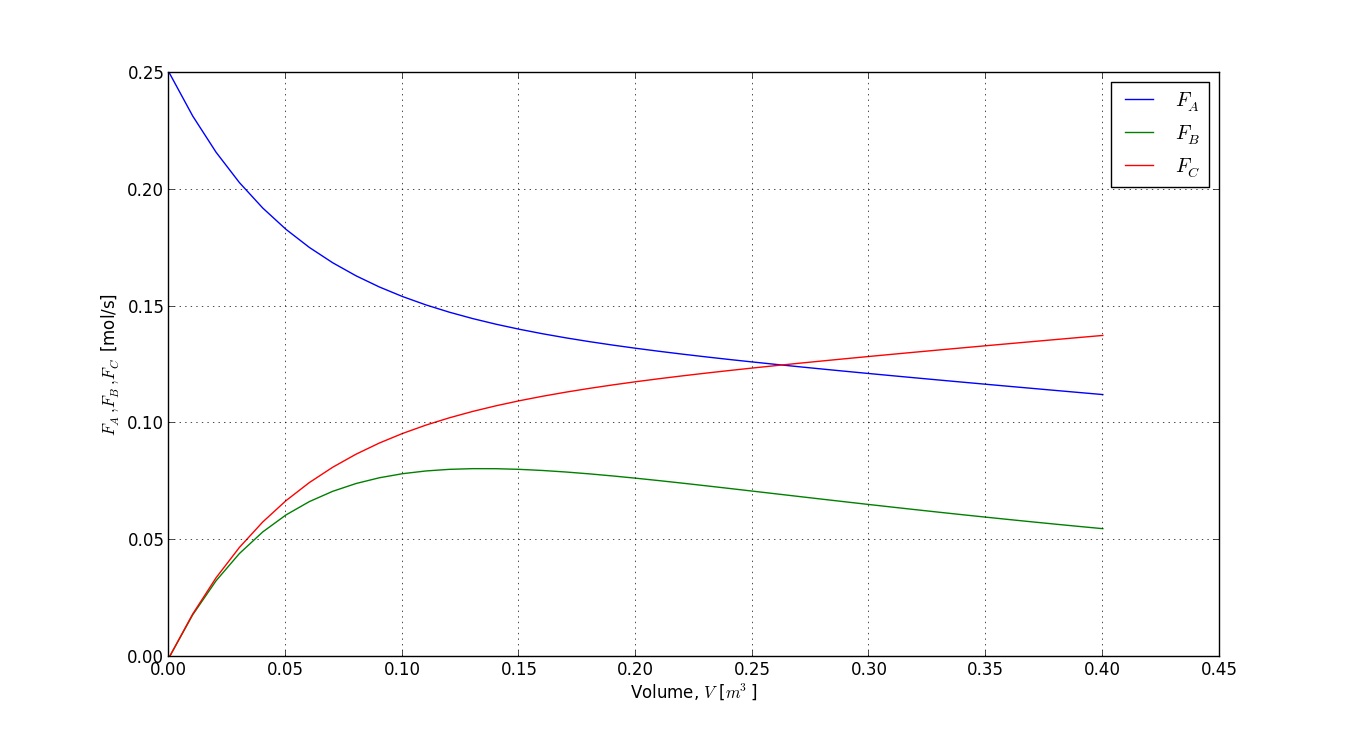
Python
import numpy as np
from scipy import integrate
from matplotlib.pylab import (plot, grid, xlabel, ylabel, show, legend)
def membrane(indep, depnt):
"""
Dynamic balance for the membrane reactor; class 07A
indep: the independent ODE variable, such as time or length
depnt: a vector of dependent variables
X = depnt[0] = the conversion
y = depnt[1] = the pressure ratio = P/P_0 = y
Returns d(depnt)/d(indep) = a vector of ODEs
"""
# Assign some variables for convenience of notation
FA = depnt[0]
FB = depnt[1]
FC = depnt[2]
# Constants
kDiff = 0.005 # s^{-1}
k = 0.01 # s^{-1}
KC = 50 # mol.m^{-3}
P0 = 830600 # Pa
T0 = 500 # K
R = 8.314 # J/(mol.K)
# Algebraic equations
FT = FA + FB + FC
CT0 = P0 / (R * T0)
CA = CT0 * FA / FT
CB = CT0 * FB / FT
CC = CT0 * FC / FT
R_B = kDiff * CB
rA = -k * (CA - CB * CC / KC)
rB = -rA
rC = -rA
# Output from this ODE function must be a COLUMN vector, with n rows
n = len(depnt)
d_depnt__d_indep = np.zeros((n,1))
d_depnt__d_indep[0] = rA
d_depnt__d_indep[1] = rB - R_B
d_depnt__d_indep[2] = rC
return d_depnt__d_indep
# The "driver" that will integrate the ODE(s):
# -----------
# Start by specifying the integrator:
# use ``vode`` with "backward differentiation formula"
r = integrate.ode(membrane).set_integrator('vode', method='bdf')
# Set the independent variable's range
indep_start = 0.0 # m^3
indep_final = 0.4 # m^3
delta = 0.01 # the results will be shown only at these ``delta`` points
num_steps = np.floor((indep_final - indep_start)/delta) + 1 # Number of steps: 1 extra for initial condition
# Set initial condition(s): for integrating variables (dependent variables)
FA_depnt_zero = 0.25 # i.e. FA(V=0) = 15 mol/min = 0.25 mol/s
FB_depnt_zero = 0.0 # i.e. FB(V=0) = 0 mol/s
FC_depnt_zero = 0.0 # i.e. FC(V=0) = 0 mol/s
r.set_initial_value([FA_depnt_zero, FB_depnt_zero, FC_depnt_zero], indep_start)
# Create vectors to store trajectories
V = np.zeros((num_steps, 1))
FA = np.zeros((num_steps, 1))
FB = np.zeros((num_steps, 1))
FC = np.zeros((num_steps, 1))
V[0] = indep_start
FA[0] = FA_depnt_zero
FB[0] = FB_depnt_zero
FC[0] = FC_depnt_zero
# Integrate the ODE(s) across each delta
k = 1
while r.successful() and k < num_steps:
r.integrate(r.t + delta)
# Store the results to plot later
V[k] = r.t
FA[k] = r.y[0]
FB[k] = r.y[1]
FC[k] = r.y[2]
k += 1
# All done! Plot the trajectories:
plot(V, FA)
grid('on')
plot(V, FB)
plot(V, FC)
xlabel('Volume, $V$ [$m^3$]')
ylabel('$F_A, F_B, F_C$ [mol/s]')
legend(['$F_A$', '$F_B$', '$F_C$'])
show()
Polymath
d(FA)/d(V) = rA
d(FB)/d(V) = rB - RB
d(FC)/d(V) = rC
FA(0) = 0.25 # mol/s
FB(0) = 0.0 # mol/s
FC(0) = 0.0 # mol/s
# Independent variable
V(0) = 0
V(f) = 0.4 #m^3
# Constants
kDiff = 0.005 # s^{-1}
k = 0.01 # s^{-1}
KC = 50 # mol.m^{-3}
P0 = 830600 # Pa
T0 = 500 # K
R = 8.314 # J/(mol.K)
# Algebraic equations
FT = FA + FB + FC
CT0 = P0 / (R * T0)
CA = CT0 * FA / FT
CB = CT0 * FB / FT
CC = CT0 * FC / FT
RB = kDiff * CB
rA = -k * (CA - CB * CC / KC)
rB = -rA
rC = -rA