2.6. Binary (Bernoulli) distribution¶
Systems that have binary outcomes (pass/fail; yes/no) must obey the probability principle that: \(p(\text{pass}) + p(\text{fail}) = 1\). That is, the sum of the probabilities of the two possible outcomes must add up to exactly one. A Bernoulli distribution only has a single parameter, \(p_1\), the probability of observing event 1. The probability of the second event is the difference with 1: that is \(p_2 = 1 - p_1\).
An example: a histogram for a system that produces 70% acceptable product, \(p(\text{pass}) = 0.7\), could look like:
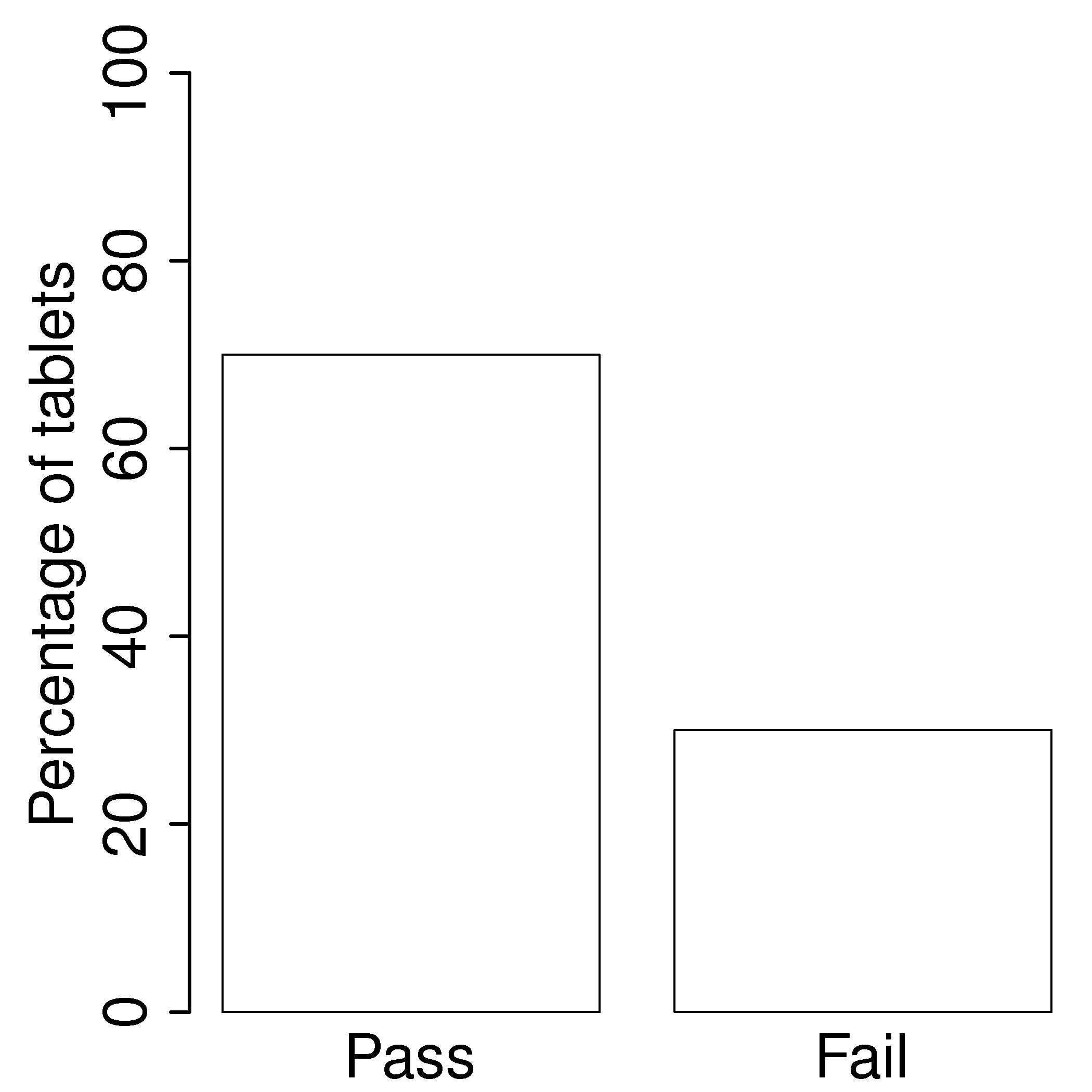
If each observation is independent of the other, then:
For the above system where \(p(\text{pass}) = 0.7\), what is probability of seeing the following sequential outcomes: pass, pass, pass (3 times in a row)?
\((0.7)(0.7)(0.7) = 0.343\), about one third
What is the probability of seeing the sequence: pass, fail, pass, fail, pass, fail?
\((0.7)(0.3)(0.7)(0.3)(0.7)(0.3) = 0.0093\), less than 1%
Another example: you work in a company that produces tablets. The machine creates acceptable, unbroken tablets 97% of the time, so \(p_\text{acceptable} = 0.97\), so \(p_\text{defective} = 0.03\).
In a future batch of 850,000 tablets, how many tablets are expected to be defective? (Most companies will call this quantity “the cost of waste”.)
\(850000 \times (1-0.97) = 25500\) tablets per batch will be defective
You take a random sample of \(n\) tablets from a large population of \(N\) tablets. What is the chance that all \(n\) tablets are acceptable if \(p\) is the Bernoulli population parameter of finding acceptable tablets:
Sample size
\(p\) = 95%
\(p\) = 97%
\(n=10\)
\(n=50\)
\(n=100\)
Are you surprised by the large reduction in the number of defective tablets for only a small increase in \(p\)? It is for this reason that a well-performing process producing accetable product does not need to have inspection of every product produced.