5.14. Extended topics related to designed experiments¶
This section is just an overview of some interesting topics, together with references to guide you to more information.
5.14.1. Experiments with mistakes, missing values, or belatedly discovered constraints¶
Many real experiments do not go smoothly. Once the experimenter has established their
But if the operator mistakenly sets the temperature to
Similarly, it might be discovered that temperature cannot be set to 475K when the other factor, for example concentration, is also at its high level. This might be due to physical or safety constraints. On the other hand,
Also see the section on optimal designs for how one can add one or more additional experiments to fix an existing bad set of experiments.
The other case that happens occasionally is that samples are lost, or the final response value is missing for some reason. Not everything is lost: recall the main effects for a full
If one or more experiments have missing
The above discussion illustrates clearly our preference for using the least squares model: whether the experimental design was executed accurately or not: the least squares model always works, whereas the short cut tools developed for perfectly executed experiments will fail.
5.14.2. Handling of constraints¶
Most engineering systems have limits of performance, either by design or from a safety standpoint. It is also common that optimum production levels are found close to these constraints. The factorials we use in our experiments must, by necessity, span a wide range of operation so that we see systematic change in our response variables, and not merely measure noise. These large ranges that we choose for the factors often hit up again constraints.
A simple bioreactor example for 2 factors is shown: at high temperatures and high substrate concentrations we risk activating a different, undesirable side-reaction. The shaded region represents the constraint where we may not operate. We could for example replace the
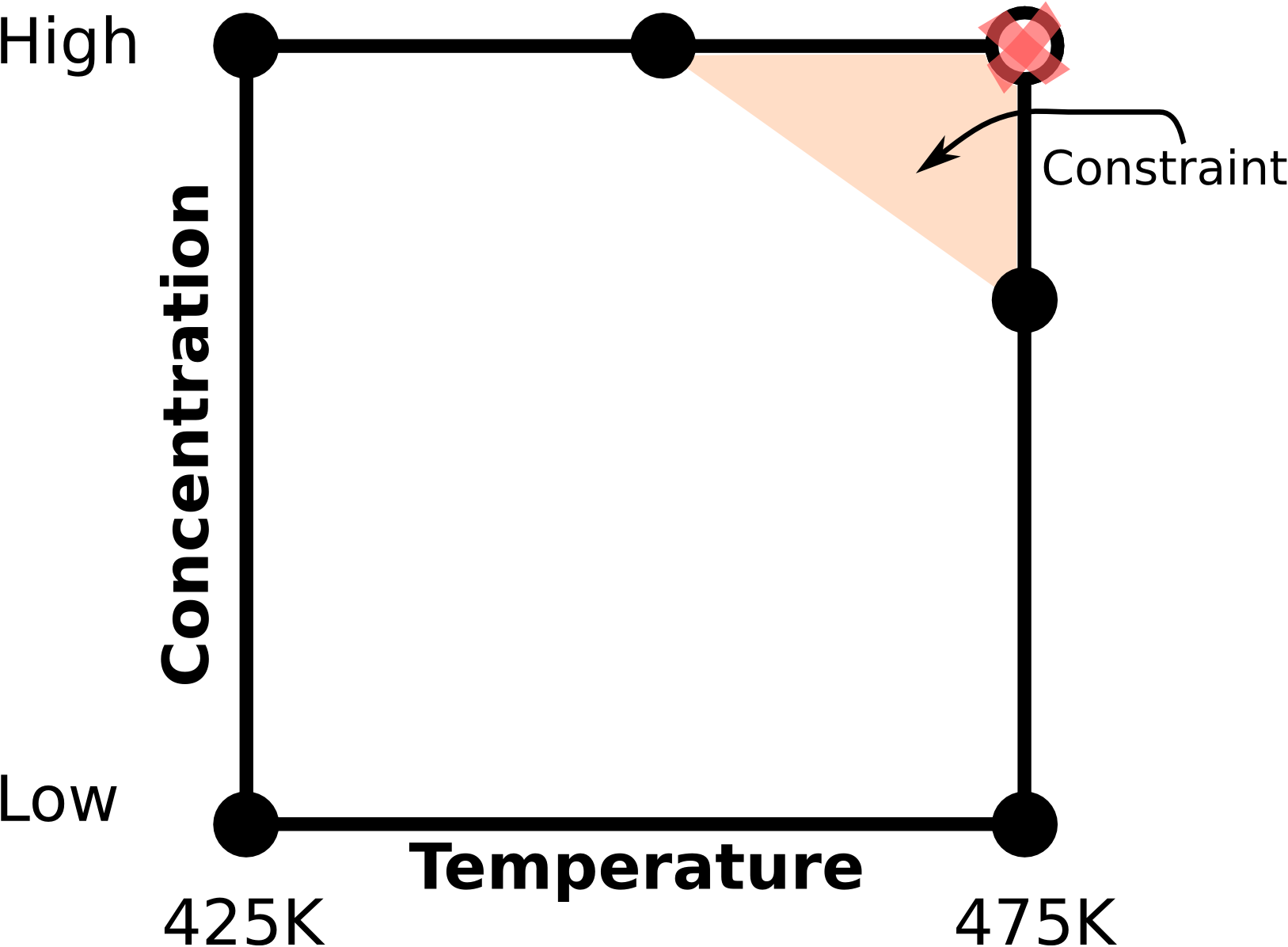
Unfortunately, these 5 runs do not form an orthogonal (independent)
It is easy to find experiments that obey the constraints for 2-factor cases: run them on the corner points. But for 3 or more factors the constraints form planes that cut through a cube. We then use optimal designs to determine where to place our experiments. A D-optimal design works well for constraint-handling because it finds the experimental points that would minimize the loss of orthogonality (i.e. they try to achieve the most orthogonal design possible). A compact way of stating this is to maximize the determinant of
These designs are generated by a computer, using iterative algorithms. See the D-optimal reference in the section on optimal designs for more information.
5.14.3. Optimal designs¶
If you delve into the modern literature on experimental methods you will rapidly come across the concept of an optimal design. This begs the question, what is sub-optimal about the factorial designs we have focussed on so far?
A full factorial design spans the maximal space possible for the
So again, what is sub-optimal about a factorial design? A factorial design is an excellent design in most cases. But if there are constraints that must be obeyed, or if the experimenter has an established list of possible experimental points to run, but must choose a subset from the list, then an “optimal” design is useful.
All an optimal design does is select the experimental points by optimizing some criterion, subject to constraints. Some examples:
The design region is a cube with a diagonal slice cut-off on two corner due to constraints. What is the design that spans the maximum volume of the remaining cube?
The experimenter wishes to estimate a non-standard model, e.g.
for fixed values of and . For a central composite design, or even a factorial design with constraints, find a smaller number of experiments than required for the full design, e.g. say 14 experiments (a number that is not a power of 2).
The user might want to investigate more than 2 levels in each factor.
The experimenter has already run
experiments, but wants to add one or more additional experiments to improve the parameter estimates, i.e. decrease the variance of the parameters. In the case of a D-optimal design, this would find which additional experiment(s) would most increase the determinant of the matrix.
The general approach with optimal designs is
The user specifies the model (i.e. the parameters).
The computer finds all possible combinations of factor levels that satisfy the constraints, including center-points. These are now called the candidate points or candidate set, represented as a long list of all possible experiments. The user can add extra experiments they would like to run to this list.
The user specifies a small number of experiments they would actually like to run.
The computer algorithm finds this required number of runs by picking entries from the list so that those few runs optimize the chosen criterion.
The most common optimality criteria are:
A-optimal designs minimize the average variance of the parameters, i.e. minimizes
D-optimal designs minimize the general variance of the parameters, i.e. maximize
G-optimal designs minimize the maximum variance of the predictions
V-optimal designs minimize the average variance of the predictions
It must be pointed out that a full factorial design,
The algorithms used to find the subset of experiments to run are called candidate exchange algorithms. They are usually just a brute force evaluation of the objective function by trying all possible combinations. They bring a new trial combination into the set, calculate the objective value for the criterion, and then iterate until the final candidate set provides the best objective function value.
Readings
St. John and Draper: “D-Optimality for Regression Designs: A Review”, Technometrics, 17, 15-, 1975.
5.14.4. Definitive screening designs¶
The final type of design to be aware of is a class of designs called the definitive screening design, and below is a link that you can read up some more information.
These designs are a type of optimal design. Optimal designs can be very flexible. For example, if you had a limited budget you can create an optimal design for a given number of factors you are investigating to maximize one of these optimality criteria to fit your budget. A computer algorithm is used to find the settings for each one of the budgeted number of runs, so that the optimization criterion is maximized. In other words the computer is designing the experiments for you, so they have some very distinct advantages.
The readings below give more details, and a practical implementation of these designs using the R software package.
Readings
John Lawson “DefScreen: Definitive Screening Designs, in package “daewr”: Design and Analysis of Experiments with R”.
Bradley Jones: “Class of Three-Level Designs for Definitive Screening in the Presence of Second-Order Effects”, Journal of Quality Technology, 2011.
5.14.5. Mixture designs¶
The area of mixture designs is incredibly important for optimizing recipes, particularly in the area of fine chemicals, pharmaceuticals, food manufacturing, and polymer processing. Like factorial designs, there are screening and optimization designs for mixtures also.
A mixture design is required when the factors being varied add up to 100% to form a mixture. Then these factors cannot be adjusted in an independent, factorial-like manner, since their proportion in the recipe must add to 100%:
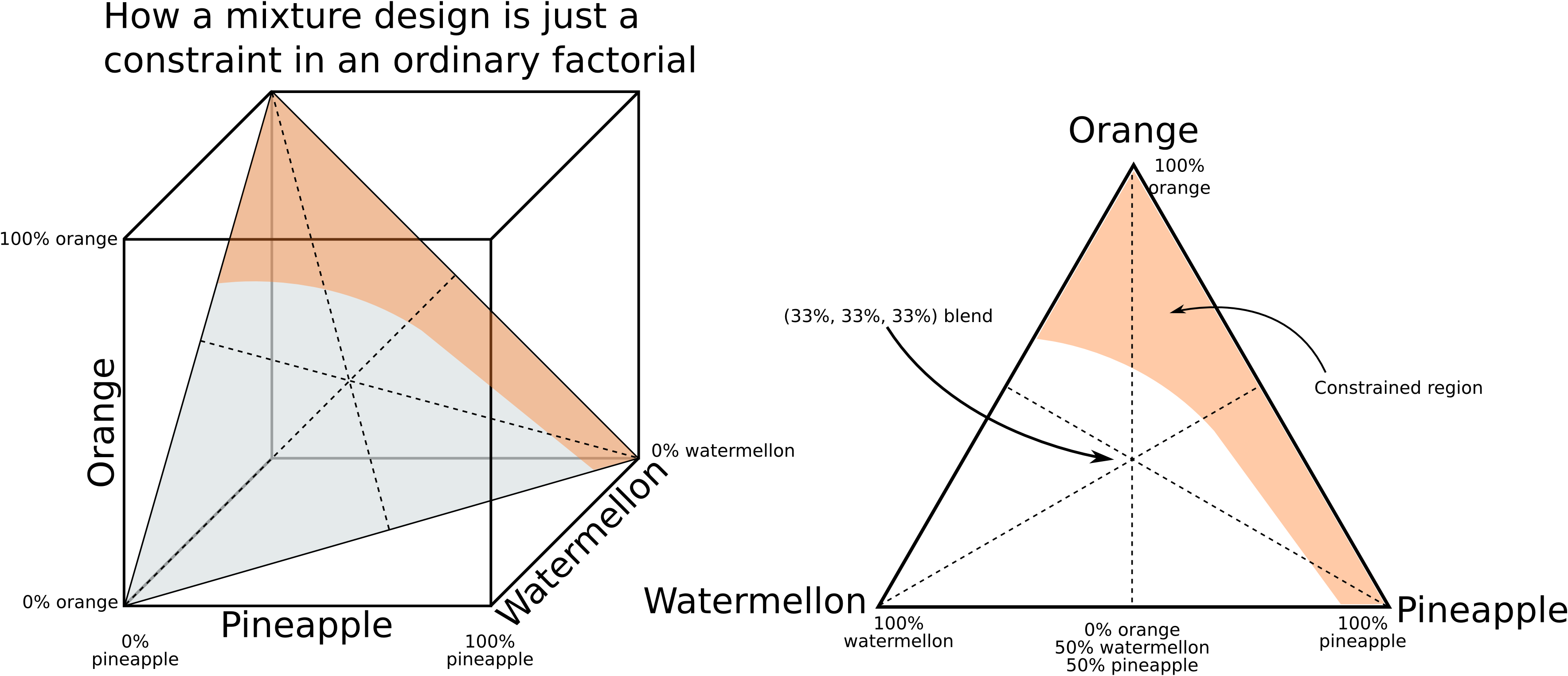
In the above figure on the right, the shaded region represents a constraint that cannot be operated in. A D-optimal algorithm must then be used to select experiments in the remaining region. The example is for finding the lowest cost mixture for a fruit punch, while still meeting certain taste requirements (e.g. watermelon juice is cheap, but has little taste). The constraint represents a region where the acidity is too high.