5.8.1. Using two levels for two or more factors¶
Let’s take a look at the mechanics of factorial designs by using our previous example where the conversion,
The range over which they will be varied is given in the table. This range was identified by the process operators as being sufficient to actually show a difference in the conversion, but not so large as to move the system to a totally different operating regime (that’s because we will fit a linear model to the data).
Factor
Low level,
High level,
Temperature,
338 K
354 K
Substrate level,
1.25 g/L
1.75 g/L
Write down the factors that will be varied:
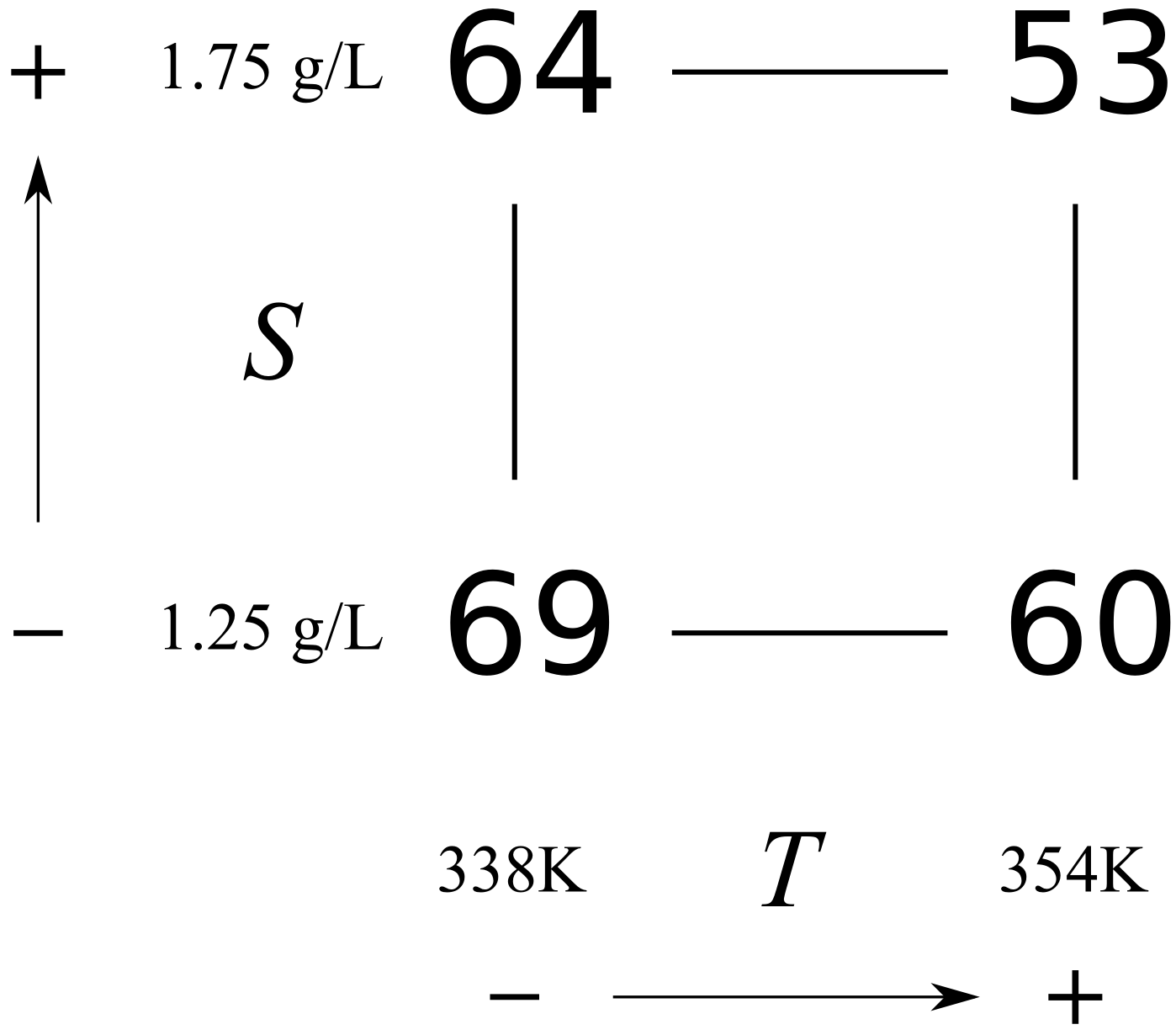
Write down the coded runs in standard order, also called Yates order, which alternates the sign of the first variable the fastest and the last variable the slowest. By convention we start all runs at their low levels and finish off with all factors at their high levels. There will be
Experiment
1
2
3
4
Add an additional column to the table for the response variable. The response variable is a quantitative value,
Experiment
Order
1
3
69
2
2
60
3
4
64
4
1
53
Experiments were performed in random order; in this case, we happened to run experiment 4 first and experiment 3 last.
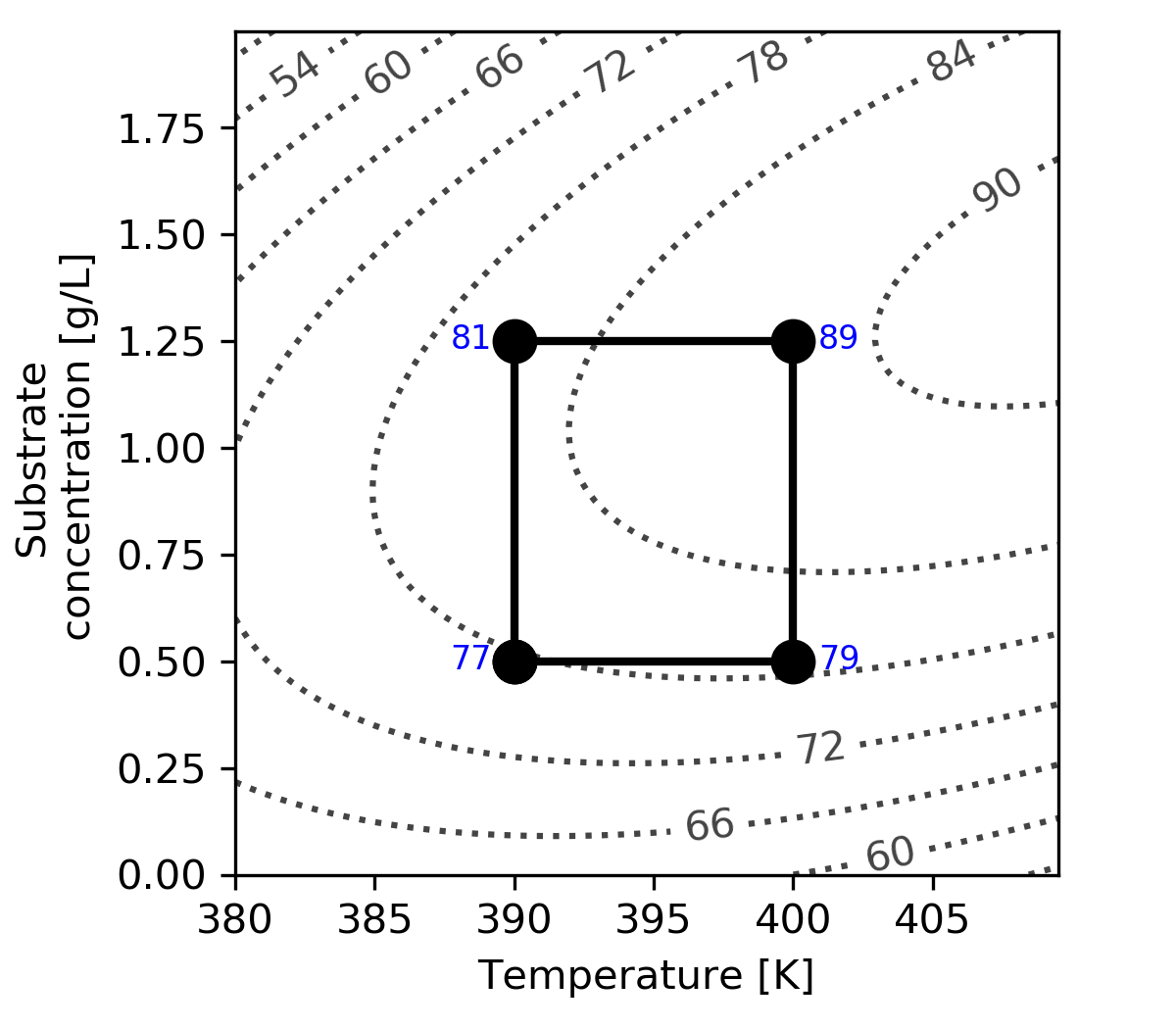
For simple systems you can visualize the design and results as shown in the following figure. This is known as a cube plot.
5.8.2. Analysis of a factorial design: main effects¶
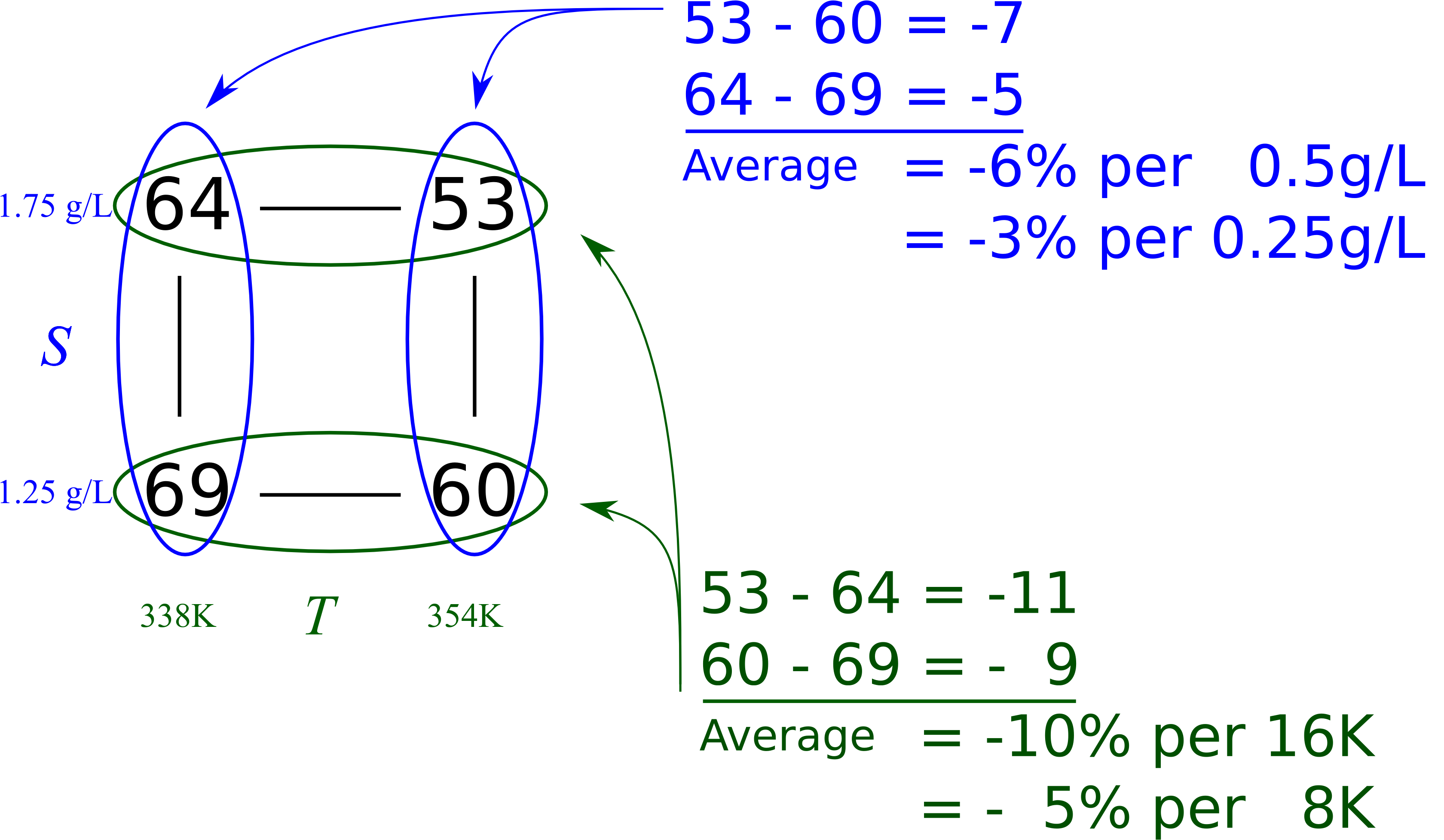
The first step is to calculate the main effect of each variable. The effects are considered, by convention, to be the difference from the high level to the low level. So the interpretation of a main effect is by how much the outcome,
Consider the two runs where
Runs 3 and 4 both have
We can perform a similar calculation for the main effect of substrate concentration,
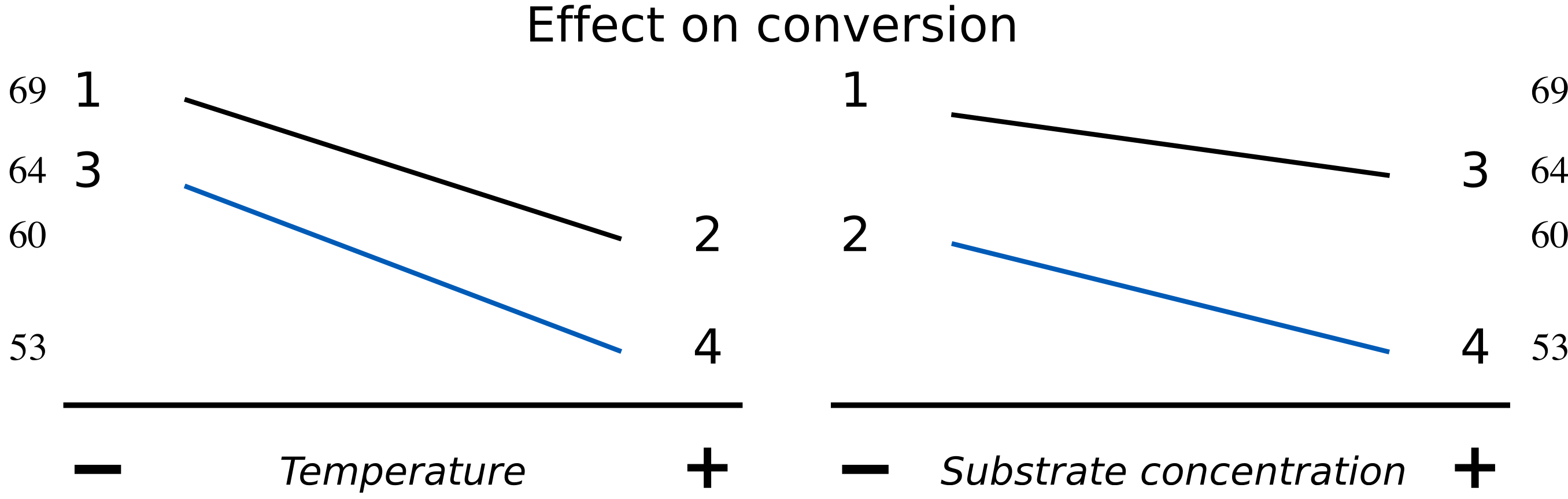
This visual summary is a very effective method of seeing how the system responds to the two variables. We can see the gradients in the system and the likely region where we can perform the next experiments to improve the bioreactor’s conversion.
The following surface plot illustrates the true, but unknown, surface from which our measurements are taken. Notice the slight curvature on the edges of each face. The main effects estimated above are a linear approximation of the conversion over the region spanned by the factorial.
An interaction plot is an alternative way to visualize these main effects. Use this method when you don’t have computer software to draw the surfaces. [We saw this earlier in the visualization section]. We will discuss interaction plots more in the next section. Here is an illustration of one such plot for a system with little interaction.
5.8.3. Analysis of a factorial design: interaction effects¶
We expect in many real systems that the main effect of temperature,
We call this result an interaction, when the effect of one factor is different at different levels of the other factors. Let’s give a practical, everyday example: assume your hands are covered with dirt or oil. We know that if you wash your hands with cold water, it will take longer to clean them than washing with hot water. So let factor A be the temperature of the water; factor A has a significant effect on the time taken to clean your hands.
Consider the case when washing your hands with cold water. If you use soap with cold water, it will take less time to clean your hands than if you did not use soap. It is clear that factor B, the categorical factor of using no soap vs some soap, will reduce the time to clean your hands.
Now consider the case when washing your hands with hot water. The time taken to clean your hands with hot water when you use soap is greatly reduced, far faster than any other combination. We say there is an interaction between using soap and the temperature of the water. This is an example of an interaction that works to help us reach the objective faster.
The effect of warm water enhances the effect of soap. Conversely, the effect is soap is enhanced by using warm water. So symmetry means that if soap interacts with water temperature, then we also know that water temperature interacts with soap.
In summary, interaction means the effect of one factor depends on the level of the other factor. In this example, that implies the effect of soap is different, depending on if we use cold water or hot water. Interactions are also symmetrical. The soap’s effect is enhanced by warm water, and the warm water’s effect is enhanced by soap.
Let’s use a different system here to illustrate interaction effects, but still using
The main effect of temperature for this system is
per 10 K
per 10 K
which means that the average temperature main effect is 5% per 10 K.
Notice how different the main effect is at the low and high levels of
Similarly, the main effect of substrate concentration is
per 0.75 g/L
per 0.75 g/L
which gives the average substrate concentration main effect as 7% per 0.75 g/L.
The data may also be visualized using an interaction plot here, showing a higher degree of interaction.
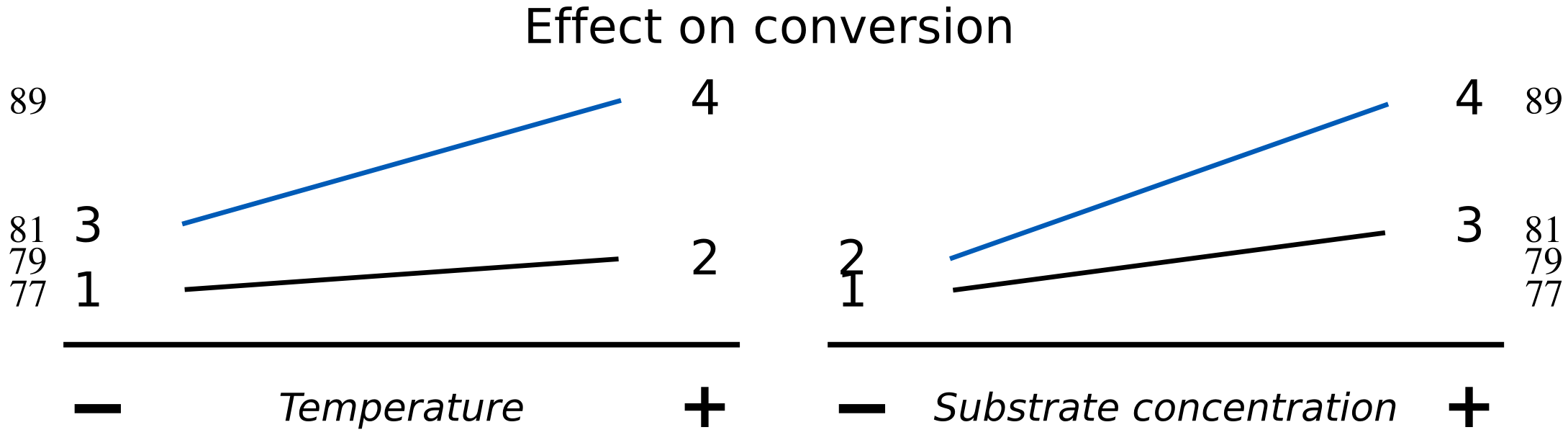
The lack of parallel lines is a clear indication of interaction. The temperature effect is stronger at high levels of
This interaction term should be zero for systems with no interaction, which implies the lines are parallel in the interaction plot. Such systems will have roughly the same effect of
We can quantify the interaction of our current example in this way. For the
Change in conversion due to
at high : Change in conversion due to
at low : The half difference:
For the
Change in conversion due to
at high : Change in conversion due to
at low : The half difference:
A large, positive interaction term indicates that temperature and substrate concentration will increase conversion by a greater amount when both
We will get an improved appreciation for interpreting main effects and the interaction effect when we consider the analysis in the form of a linear, least squares model.