5.8.6. Assessing significance of main effects and interactions¶
When there are no replicate points, then the number of factors to estimate from a full factorial is
The standard error can be estimated if complete replicates are available. However, a complete replicate is onerous, because a complete replicate implies the entire experiment is repeated: system setup, running the experiment and measuring the result. Taking two samples from one actual experiment and measuring
Furthermore, there are better ways to spend our experimental budget than running complete replicate experiments – see the section on screening designs later on. Only later in the overall experimental procedure should we run replicate experiments as a verification step and to assess the statistical significance of effects.
There are two main ways we can determine if a main effect or interaction is significant: by using a Pareto plot or the standard error.
5.8.6.1. Pareto plot¶
Note
This is a makeshift approach that is only applicable if all the factors are centered and scaled.
A full factorial with
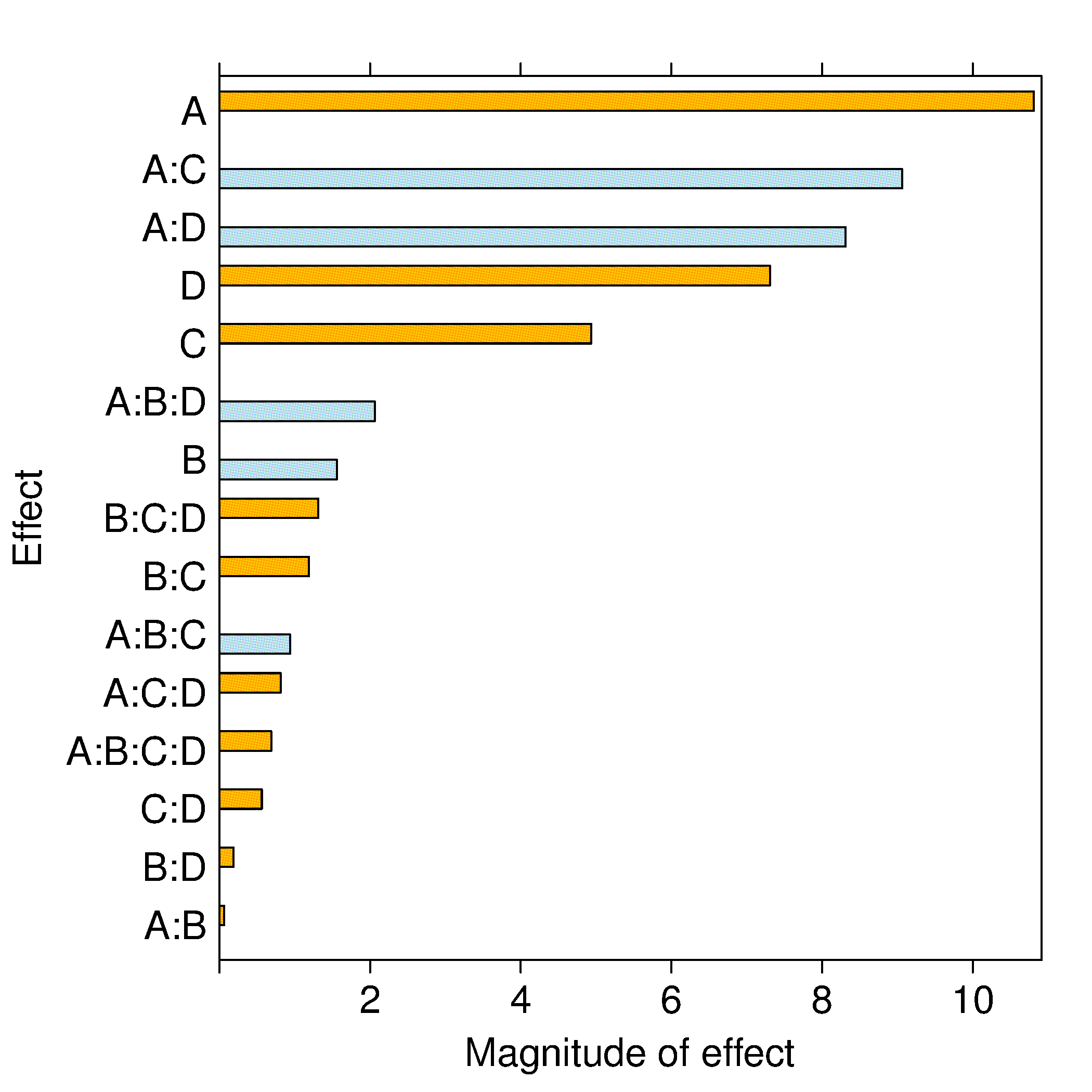
The example shown in the bar graph was from a full factorial experiment where the results for
We would interpret that factors A, C and D, as well as the interactions of AC and AD, have a significant and causal effect on the response variable,
The reason why we can compare the coefficients this way, which is not normally the case with least squares models, is that we have both centered and scaled the factor variables. If the centering is at typical baseline operation, and the range spanned by each factor is that expected over the typical operating range, then we can fairly compare each coefficient in the bar plot. Each bar represents the influence of that term on
Obviously, if the factors are not scaled appropriately, then this method will be error prone. However, the approximate guidance is accurate, especially when you do not have a computer or if additional information required by the other methods (discussed below) is not available. It is also the only way to estimate the effects for highly fractionated and saturated designs.
5.8.6.2. Standard error: from replicate runs or from an external dataset¶
Note
It is often better to spend your experimental budget screening for additional factors rather than replicating experiments.
If there are more experiments than parameters to be estimated, then we have extra degrees of freedom. Having degrees of freedom implies we can calculate the standard error,
For an experiment with
A
factorial where every combination has been repeated will have runs, so the standard error for each coefficient will be the same, at . A
factorial with three additional runs at the center point would have the following least squares representation: And substituting in the values, using vector shortcut notation for
and : Note that the center point runs do not change the orthogonality of
(verify this by writing out and computing the matrix and observing that all off-diagonal entries are zeros). However, as we expect after having studied the section on least squares modelling, additional runs decrease the variance of the model parameters, . In this case, there are runs, so the standard error is decreased to . However, the center points do not further reduce the variance of the parameters in , because the denominator is still (except for the intercept term, whose variance is reduced by the center points).
Once we obtain the standard error for our system and calculate the variance of the parameters, we can multiply it by the critical
Even though the confidence interval of the temperature effect would be
5.8.6.3. Refitting the model after removing nonsignificant effects¶
After having established which effects are significant, we can exclude the nonsignificant effects and increase the degrees of freedom. (We do not have to recalculate the model parameters – why?) The residuals will be nonzero now, so we can then estimate the standard error and apply all the tools from least squares modelling to assess the residuals. Plots of the residuals in experimental order, against fitted values, q-q plots and all the other assessment tools from earlier are used, as usual.
Continuing the above example, where a qt(0.975, df=11) = 2.2. So the confidence intervals can be calculated to confirm that these are indeed significant effects.
There is some circular reasoning here: postulate that one or more effects are zero and increase the degrees of freedom by removing those parameters in order to confirm the remaining effects are significant. Some general advice is to first exclude effects that are definitely small, and then retain medium-size effects in the model until you can confirm they are not significant.
5.8.6.4. Variance of estimates from the COST approach versus the factorial approach¶
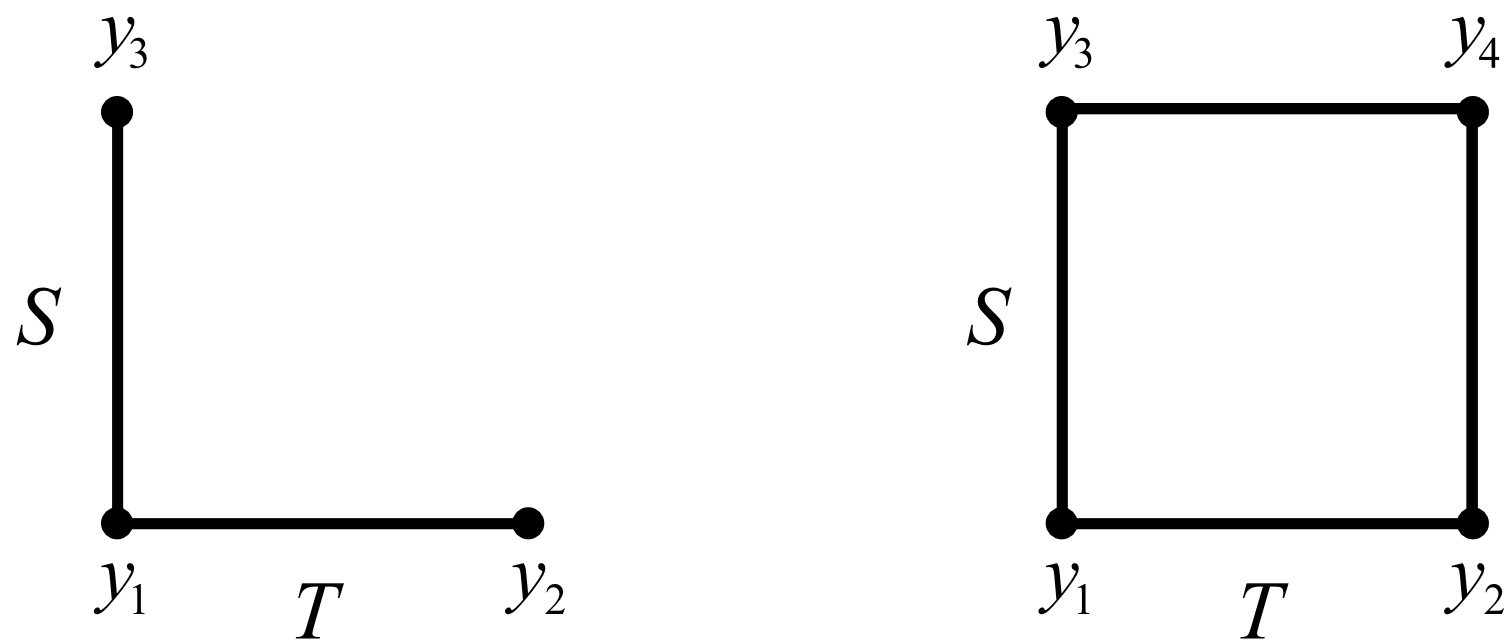
Finally, we end this section on factorials by illustrating their efficiency. Contrast the two cases: COST and the full factorial approach. For this analysis we define the main effect simply as the difference between the high and low values (normally we divide through by 2, but the results still hold). Define the variance of the measured
COST approach |
Fractional factorial approach |
|---|---|
The main effect of |
The main effect is |
The variance is |
The variance is |
So |
And |
Not only does the factorial experiment estimate the effects with much greater precision (lower variance), but the COST approach cannot estimate the effect of interactions, which is incredibly important, especially as systems approach optima that are on ridges (see the contour plots earlier in this section for an example).
Factorial designs make each experimental observation work twice.