6.7.1. Advantages of the projection to latent structures (PLS) method¶
So for predictive uses, a PLS model is very similar to principal component regression (PCR) models. And PCR models were a big improvement over using multiple linear regression (MLR). In brief, PCR was shown to have these advantages:
It handles the correlation among variables in
It extracts these scores
We reduce, but don’t remove, the severity of the assumption in MLR that the predictor’s,
With MLR we require that
We get the great benefit of a consistency check on the raw data, using SPE and
An important point is that PCR is a two-step process:

In other words, we replace the
The PLS model goes a bit further and introduces some additional advantages over PCR:
A single PLS model can be built for multiple, correlated
The PLS model directly assumes that there is error in
PLS is more efficient than PCR in two ways: with PCR, one or more of the score columns in
Similar to PCA, the basis for PCR, we have that PLS also extracts sequential components, but it does so using the data in both
We will get into the details shortly, but as a starting approximation, you can visualize PLS as a method that extracts a single set of scores,
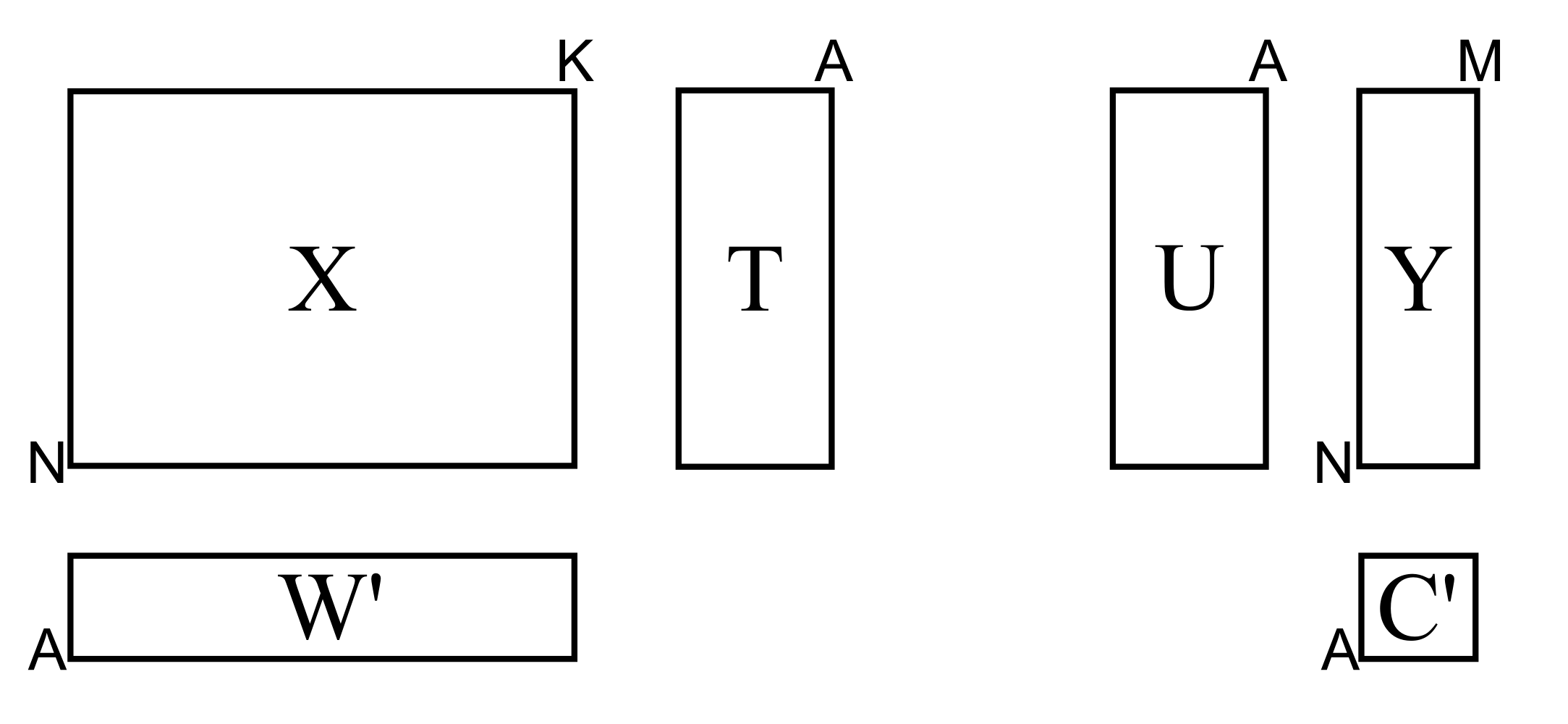
From an engineering point of view this is quite a satisfying interpretation. After all, the variables we chose to be in