5.9.2. Generators and defining relationships¶
Calculating which main effects and two-factor interactions will be confounded with each other, called the confounding pattern, can be tedious for larger values of
Recall for the half-fraction of a
D = ABC
This is called the generating relation for the design. Here are some rules when working with this notation:
A factor multiplied by itself is the identity, or intercept column: A
A factor multiplied by a column of ones is equal to itself. For example: D
The intercept I is simply a column of ones, which is what the intercept column is. And for emphasis: I
You can substitute in the generating relation of D = ABC, and like with an algebraic equation, we can multiply both sides by D to get D
This last part, I = ABCD, is called the defining relation for this design. Notice that we started with the generating relation and simplified it by multiplying the terms in that relationship with each other. Since there were two terms, ABC and D, we multiplied them, and ended up with I = ABCD.
This is our defining relationship for this design:
I = ABCD
We will discuss this topic again later with more examples. The main point though is that the effects which are aliased (confounded) with each other can be found quickly by multiplying the effect we are interested in by the defining relationship. For example, if we wanted to know what the main effect A would be confounded with in this
A = A
indicating that A is aliased with the 3-factor interaction BCD. What is the aliasing for these effects:
What is main effect B aliased with? (Answer: ACD)
What is the 2fi AC aliased with? (Answer: BD)
Another example:
Returning back to the
half fraction in the previous section, use the generating relation to verify the aliasing of main-effects and two-factor interactions derived earlier by hand.
First calculate the defining relationship. It is I = …..
Aliasing for A? (Answer: BC)
Aliasing for B? (Answer: AC)
Aliasing for C? (Answer: AB: recall this is how we generated that half fraction)
Aliasing for the intercept term, I? (Answer: ABC)
Yet another example:
Which aliasing (confounding) would occur if you decided for a
design to generate the half-fraction by using the 2-factor interaction term AC rather than the 3-factor interaction term ABC.
First write out your generating relationship: D = AC
Now calculate the defining relationship: I = ….
Aliasing for A? (Answer: CD)
Aliasing for B? (Answer: ABCD)
Aliasing for C? (Answer: AD)
Why is this a poorer choice than using D = ABC to generate the half-fraction? Answer: the main effects of A and C which could be important, are aliased with 2fi. Had we generated the design with the usual 3fi term, ABC, the main effects would only be aliased with three-factor interactions (3fi).
5.9.3. Generating the complementary half-fraction¶
Returning to our example in the previous section of a half-fraction from a full
The original generator was C = AB and the defining relation was I = ABC; so factor C was aliased with the 2fi of AB. If it was factor C that had an opposite sign, it could be due to C, or due to AB. So you wish to complete the full-factorial and run the other half fraction to find out. This will help clarify that interesting factor, because it will remove the aliasing when you then analyze all 8 data points together.
The defining relation for the complementary half-fraction is I = -ABC, or multiply both sides by C to equivalently obtain IC = C = -AB. This shows the complementary half fraction is in fact generated by C = -AB, while the original half-fraction was generated by C = AB. This is a general rule that applies to half-fractions.
Let’s return to the table in the previous section and generate the other 4 runs from that C = -AB defining relationship:
Experiment |
A |
B |
C = |
|---|---|---|---|
5 |
|||
6 |
|||
7 |
|||
8 |
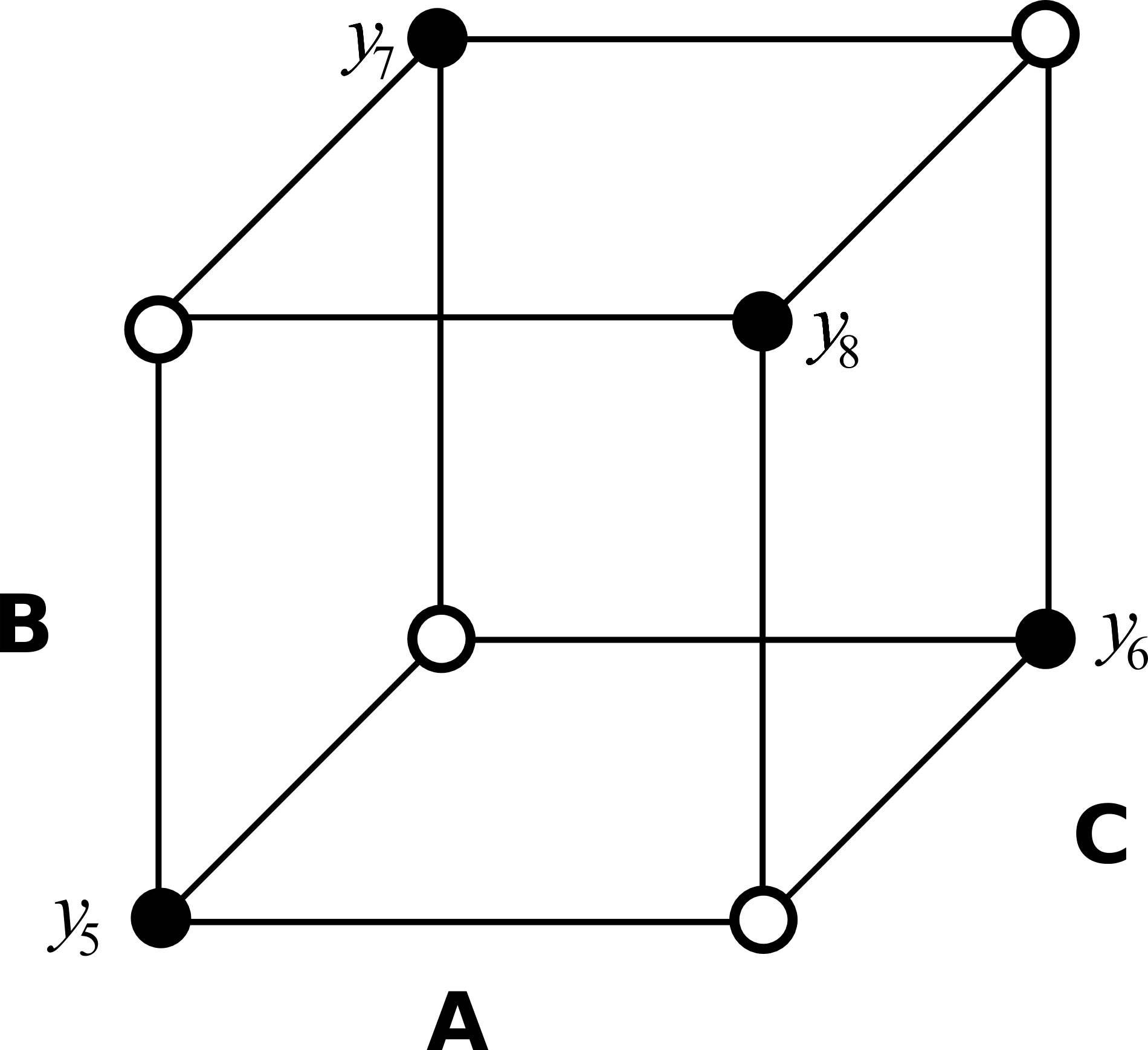
After running these additional 4 experiments shown (in random order of course) we have a complete set of 8 runs. Analyzing the data together we can calculate the main effects and two-factor interactions without aliasing because we are back to the usual full factorial of
So we see that we can always complete our half-fraction by creating a complementary fraction. This complimentary fraction is found by flipping the sign on the generating factor. For example, changing the sign from C = AB to -C = AB. In the illustration this is equivalent to running the 4 experiments at the closed circles.
5.9.4. Generators: to determine confounding due to blocking¶
Generators are also great for determining the blocking pattern. Recall the case described earlier where we only had enough material to run two sets of 4 experiments to complete our
So in general if you run a full
Here are the block generators you can use when splitting a
Design |
Block 1 defining relation |
Block 2 defining relation |
|
|---|---|---|---|
3 |
I=ABC |
I=-ABC |
|
4 |
I=ABCD |
I=-ABCD |
|
5 |
I=ABCDE |
I=-ABCDE |