4.12. Enrichment topics¶
These topics are not covered in depth in this book, but might be of interest to you. I provide a small introduction to each topic, showing what their purpose is, together with some examples.
4.12.1. Nonparametric models¶
Nonparametric modelling is a general model where the relationship between
Consider the example of plotting Prestige (the Pineo-Porter prestige score) against Income, from the 1971 Canadian census. A snippet of the data is given by:
education income women prestige census type
ECONOMISTS 14.44 8049 57.31 62.2 2311 prof
VOCATIONAL.COUNSELLORS 15.22 9593 34.89 58.3 2391 prof
PHYSICIANS 15.96 25308 10.56 87.2 3111 prof
NURSING.AIDES 9.45 3485 76.14 34.9 3135 bc
POSTAL.CLERKS 10.07 3739 52.27 37.2 4173 wc
TRAVEL.CLERKS 11.43 6259 39.17 35.7 4193 wc
BABYSITTERS 9.46 611 96.53 25.9 6147 <NA>
BAKERS 7.54 4199 33.30 38.9 8213 bc
MASONS 6.60 5959 0.52 36.2 8782 bc
HOUSE.PAINTERS 7.81 4549 2.46 29.9 8785 bc
The plot on the left is the raw data, while on the right is the raw data with the nonparametric model (line) superimposed. The smoothed line is the nonparametric function,
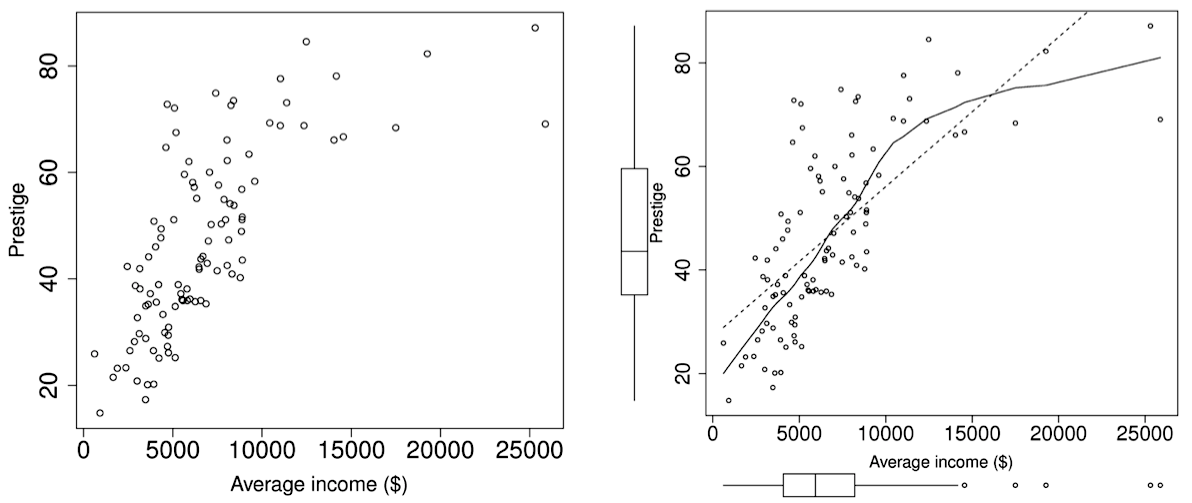
For bivariate cases, the nonparametric model is often called a scatterplot smoother. There are several methods to calculate the model; one way is by locally weighted scatterplot smoother (LOESS), described as follows. Inside a fixed subregion along the
collect the
calculate a fitted
record that average
slide the window along the
The model is the collection of these
More details can be found in W.S. Cleveland, Robust Locally Weighted Regression and Smoothing Scatterplots, Journal of the American Statistical Association, 74 (368), p. 829-836, 1979.
4.12.2. Robust least squares models¶
Outliers are often the most interesting observations and are usually the points from which we learn the most about the system. A manual step where we review the outliers and their influence should always done for any important model. For example, inspection of the residual plots as described in the preceding sections.
However, the ability to build a linear model that is not heavily influenced by outliers might be of interest in certain cases.
The model is built automatically and is not reviewed by a human (e.g. as an intermediate step in a data-mining procedure). This is increasingly common in systems that build on top of the least squares model to improve their performance in some way.
The human reviewer is not skilled to know which plots to inspect for influential and discrepant observations, or may not know how to interpret these plots.
Some criticism of robust methods are that there are too many different robust methods and that these routines are much more computationally expensive than ordinary least squares. The first point is true, as this as a rapidly evolving field, however the latter objection is not of too much concern these days. Robust methods are now available in most decent software packages, and are stabilizing towards a few reliable robust estimators.
If you would like to read up some more, a nice introduction targeted at engineering readers is given in PJ Rousseeuw’s “Tutorial to Robust Statistics”, Journal of Chemometrics, 5, 1-20, 1991.
In R the various efforts of international researchers is being consolidated. The robustbase package provides basic functionality that is now well established in the field; use that package if you want to assemble various robust tools yourself. On the other hand, a more comprehensive package called robust is also available which provides robust tools that you should use if you are not too concerned with the details of implementation.
For example:
> data <- read.csv('http://openmv.net/file/distillation-tower.csv')
# Using ordinary least squares
# -----------------------------
> summary(lm(data$VapourPressure ~ data$TempC2))
Call:
lm(formula = data$VapourPressure ~ data$TempC2)
Residuals:
Min 1Q Median 3Q Max
-5.59621 -2.37597 0.06674 2.00212 14.18660
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 195.96141 4.87669 40.18 <2e-16 ***
data$TempC2 -0.33133 0.01013 -32.69 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.989 on 251 degrees of freedom
Multiple R-squared: 0.8098, Adjusted R-squared: 0.8091
F-statistic: 1069 on 1 and 251 DF, p-value: < 2.2e-16
# Use robust least squares (with automatic selection of robust method)
# --------------------------------------------------------------------
> library(robust)
> summary(lmRob(data$VapourPressure ~ data$TempC2))
Call: lmRob(formula = data$VapourPressure ~ data$TempC2)
Residuals:
Min 1Q Median 3Q Max
-5.2631296 -1.9805384 0.1677174 2.1565730 15.8846460
Coefficients:
Value Std. Error t value Pr(>|t|)
(Intercept) 179.48579886 4.92870640 36.41641120 0.00000000
data$TempC2 -0.29776778 0.01021412 -29.15256677 0.00000000
Residual standard error: 2.791 on 251 degrees of freedom
Multiple R-Squared: 0.636099
Test for Bias:
statistic p-value
M-estimate 7.962583 0.018661525
LS-estimate 12.336592 0.002094802
In this example the two models perform similarly in terms on their
4.12.3. Logistic modelling (regression)¶
There are many practical cases in engineering modelling where our
Predict whether our product specifications are achieved (
= 0 or 1) given the batch reaction’s temperature as , the reaction duration and the reactor vessel, where for reactor A and for reactor B. Predict the likelihood of making a sale in your store (
= 0 or 1), given the customer’s age , whether they are a new or existing customers, is either 0 or 1, and the day of the week as . Predict if the final product will be
= acceptable, medium, or unsellable based on the raw material’s properties and the ambient temperature .
We could naively assume that we just code our
The predictions when using the model are not dichotomous (0 or 1), which is not too much of a problem if we interpret our prediction more as a probability. That is, our prediction is the probability of success or failure, according to how we coded it originally. However the predictions often lie outside the range
. We can attempt to compensate for this by clamping the output to zero or one, but this non-linearity causes instability in the estimation algorithms. The errors are not normally distributed.
The variance of the errors are not constant and the assumption of linearity breaks down.
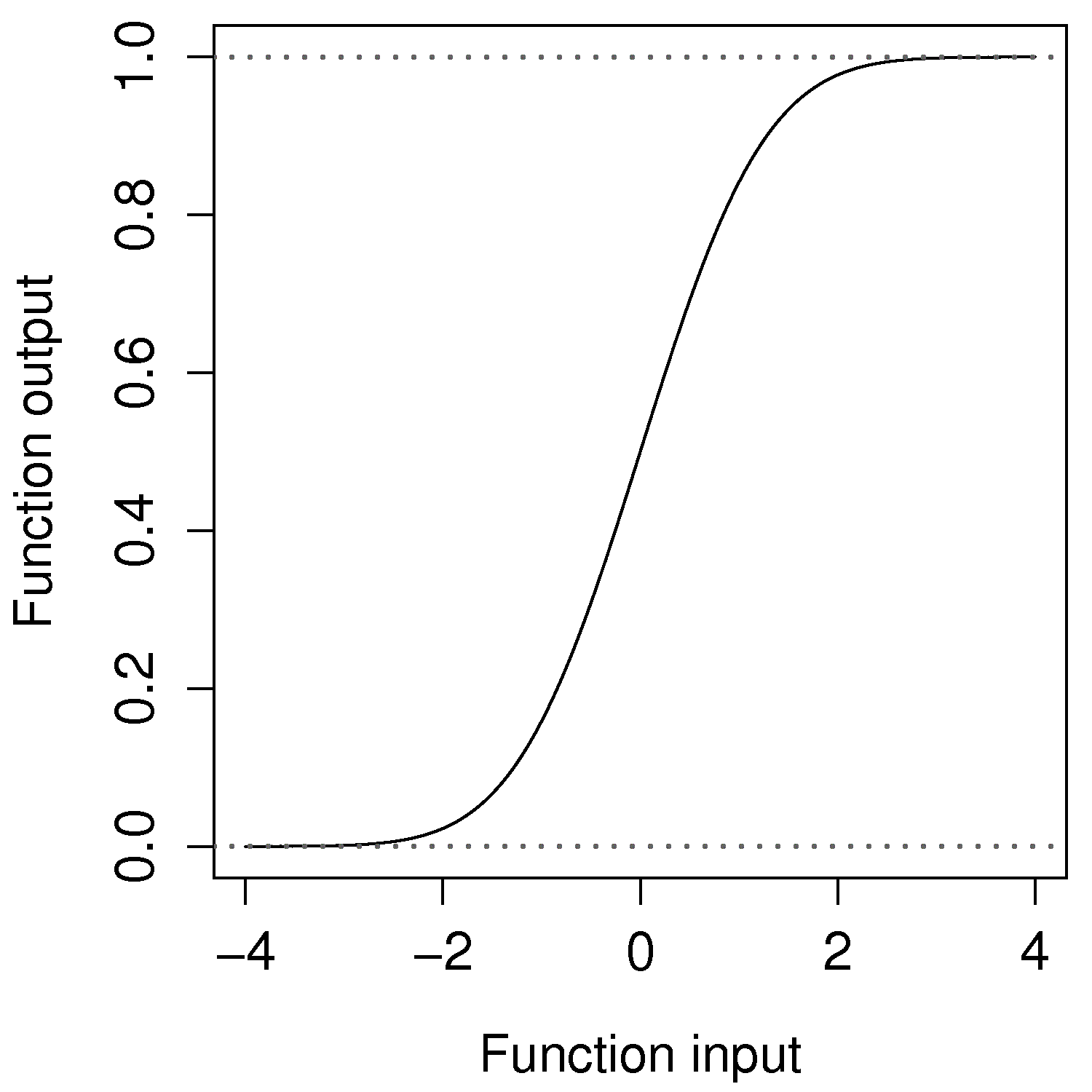
A logistic model however accounts for the nature of the y-variable by creating a function, called a logistic function, which is bounded between 0 and 1. In fact you are already familiar with such a function: the cumulative probability of the normal distribution does exactly this.
Once the glm(y ~ x1 + x2, family=binomial) function to build a model where y must be a factor variable: type help(factor) to learn more. The model output is interpreted as any other.
4.12.4. Testing of least-squares models¶
Before launching into this concept, first step back and understand why we are building least squares models. One objective is to learn more about our systems: (a) what is the effect of one variable on another, or (b) is the effect significant (examine the confidence interval). Another objective is purely predictive: build a model so that we can use it to make predictions. For this last case we must test our model’s capability for accurate predictions.
The gold standard is always to have a testing data set available to quantify how good (adequate) your least squares model is. It is important that (a) the test set has no influence on the calculation of the model parameters, and (b) is representative of how the model will be used in the future. We will illustrate this with 2 examples: you need to build a predictive model for product viscosity from 3 variables on your process. You have data available, once per day, for 2006 and 2007 (730 observations).
Use observation 1, 3, 5, 7, … 729 to build the least squares model; then use observation 2, 4, 6, 8, … 730 to test the model.
Use observations 1 to 365 (data from 2006) to build the model, and then use observations 366 to 730 (data from 2007) to test the model.
In both cases, the testing data has no influence on the model parameters. However the first case is not representative of how the model will be used in the future. The results from the first case are likely to give over-optimistic results, while the second case represents the intended use of the model more closely, and will have more honest results. Find out sooner, rather than later, that the model’s long-term performance is not what you expect. It may be that you have to keep rebuilding the model every 3 months, updating the model with the most recent data, in order to maintain it’s predictive performance.
How do we quantify this predictive performance? A common way is to calculate the root mean square of the prediction error (RMSEP), this is very similar to the standard error that we saw earlier for regression models. Assuming the errors are centered at zero and follow a normal distribution, the RMSEP can be interpreted as the standard deviation of the prediction residuals. It is important the RMSEP be calculated only from new, unseen testing data. By contrast, you might see the term RMSEE (root mean square error of estimation), which is the RMSEP, but calculated from the training (model-building) data. The RMSEE
The units of RMSEP and RMSEE are the same as the units of the
In the latent variable modelling section of the book we will introduce the concept of cross-validation to test a model. Cross-validation uses the model training data to simulate the testing process. So it is not as desirable as having a fresh testing data set, but it works well in many cases. Cross-validation can be equally well applied to least squares models. We will revisit this topic later.
4.12.5. Bootstrapping¶
Bootstrapping is an extremely useful tool when theoretical techniques to estimate confidence intervals and uncertainty are not available to us.
Let’s give an example where bootstrapping is strictly not required, but is definitely useful. When fitting a least squares model of the form
In the preceding section on least squares model analysis we derived this confidence interval for
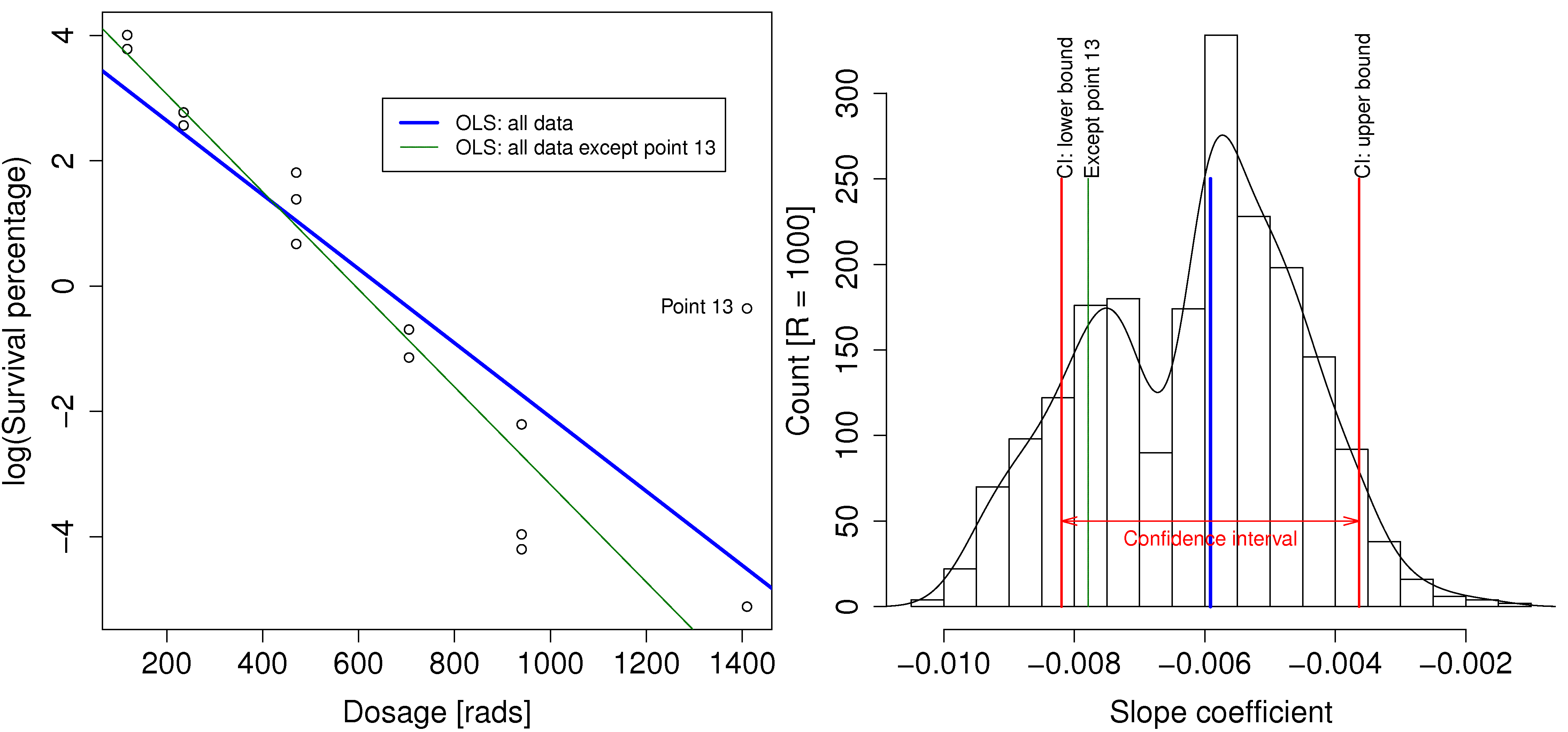
Visualize this confidence in the context of the following example where log(survival)).
The thick line represents the slope coefficient (
Bootstrapping gives us an indication of that sensitivity, as shown in the other plot. The original data set had 14 observations. What bootstrapping does is to randomly select 14 rows from the original data, allowing for duplicate selection. These selected rows are used to build a least squares model, and the slope coefficient is recorded. Then another 14 random rows are selected and this process is repeated R times (in this case R=1000). On some of these occasions the outlier points will be included, and other times they will be excluded.
A histogram of the 1000 computed slope coefficients is shown here. This histogram gives us an additional indication of the uncertainty of the slope coefficient. It shows many possible slope coefficients that could have been obtained. One in particular has been marked, the slope when point 13 was omitted.
For completeness the confidence interval at the 95% level for
This confidence interval, together with the bootstrapped values of
By now you should also be wondering whether you can bootstrap the confidence interval bounds! That’s left as exercise for interested readers. The above example was inspired from an example in ASA Statistics Computing and Graphics, 13 (1), 2002.