3.8. Process capability¶
Note
This section is not about a particular monitoring chart, but is relevant to the topic of process monitoring.
3.8.1. Centered processes¶
Purchasers of your product may request a process capability ratio (PCR) for each of the quality attributes of your product. For example, your plastic product is characterized by its Mooney viscosity and melting point. A PCR value can be calculated for either property, using the definition below:
Since the population standard deviation,
Interpretation of the PCR:
assumes the property of interest follows a normal distribution
assumes the process is centered (i.e. your long term mean is halfway between the upper and lower specification limits)
assumes the PCR value was calculated when the process was stable
The PCR is often called the process width. Let’s see why by taking a look at a process with PCR=0.5 and then PCR=2.0. In the first case
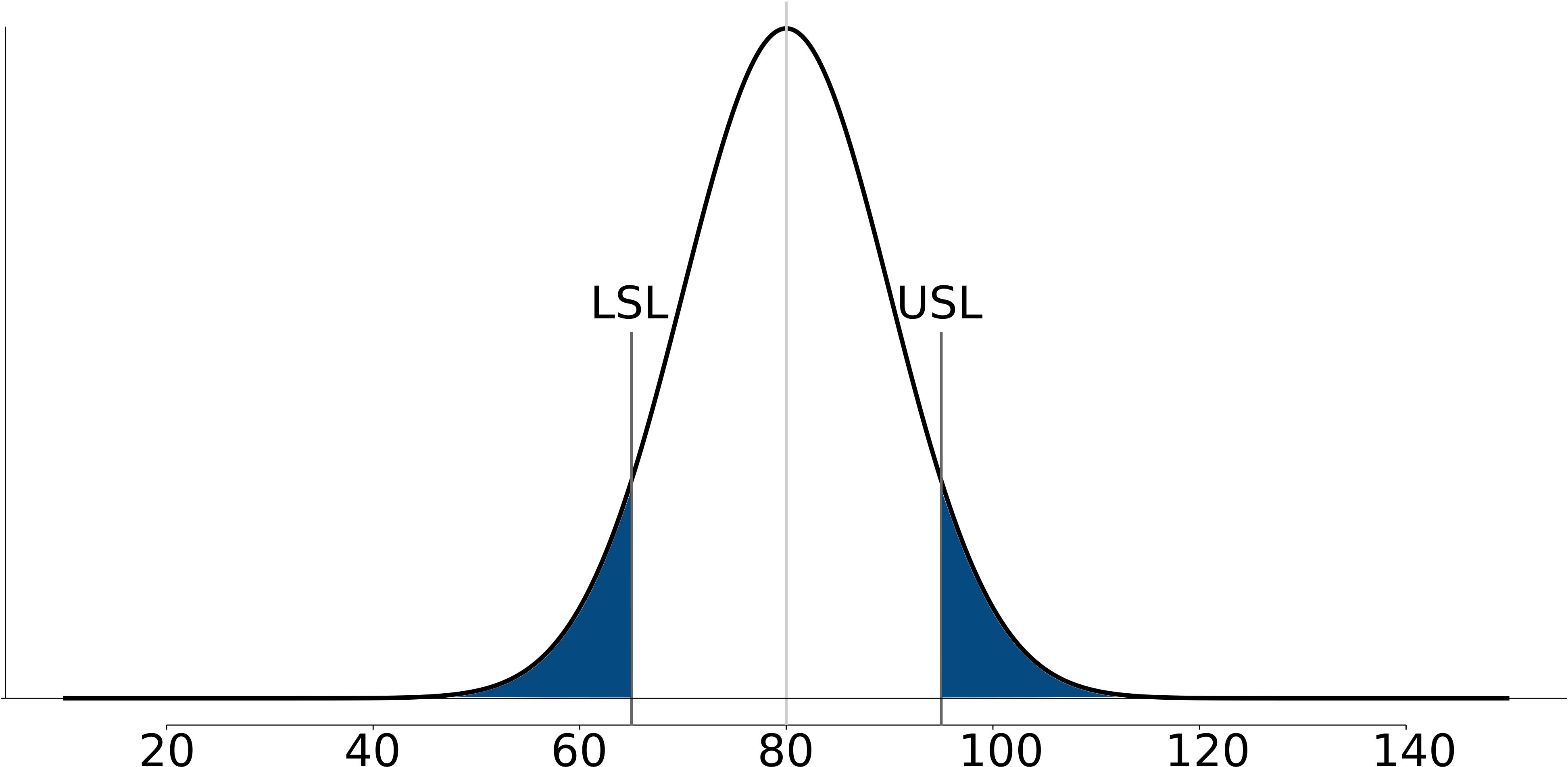
The diagram is from a process with mean of 80 and where LSL=65 and USL=95. These specification are fixed, set by our production guidelines. If the process variation is
for LSL =
for USL = Shaded area probability =
pnorm(-1.5) + (1-pnorm(1.5))= 13.4% of production is out of the specification limits.
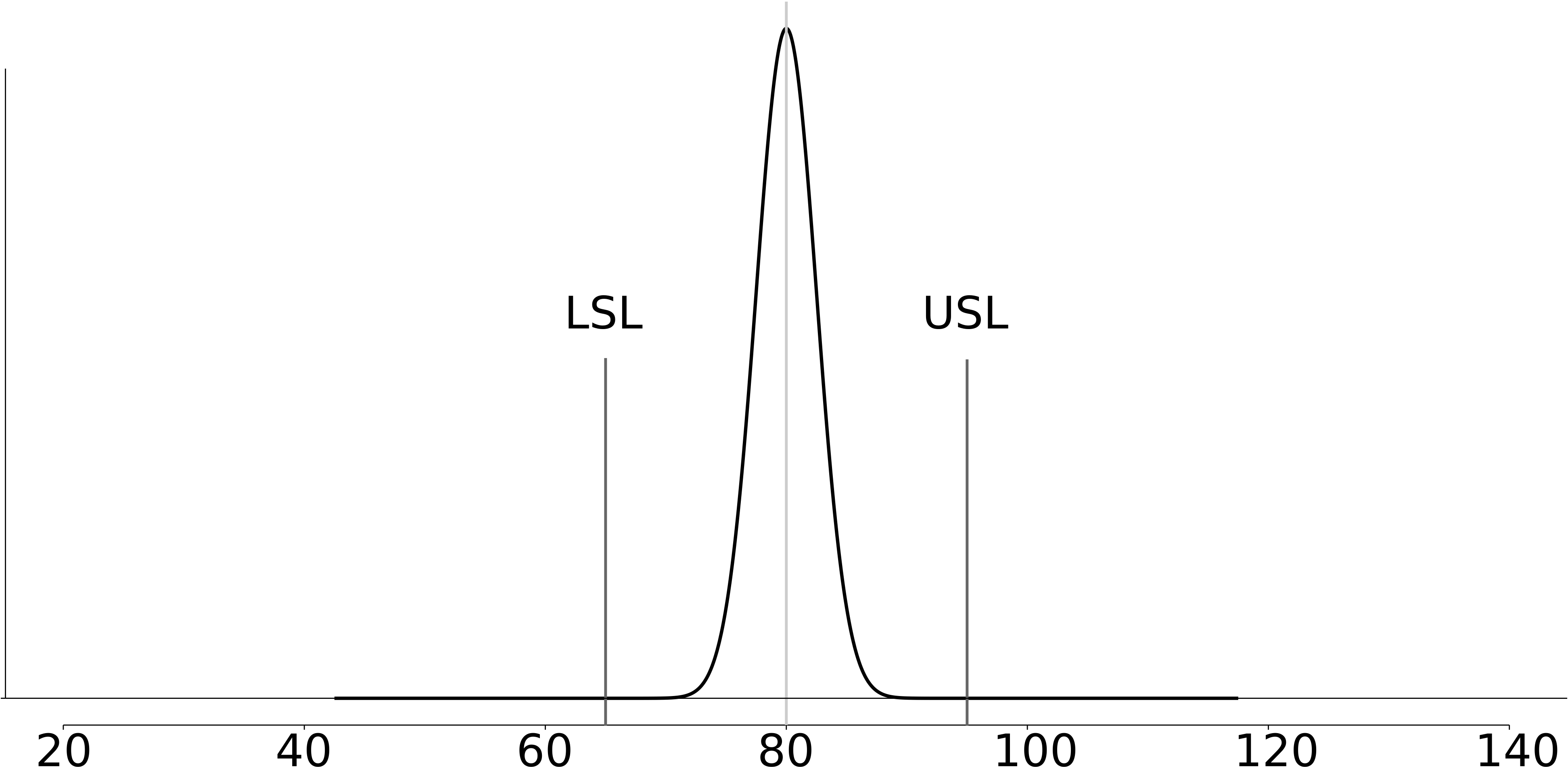
Contrast this to the case where PCR = 2.0 for the same system. To achieve that level of process capability, using the same upper and lower specifications we have to reduce the standard deviation by a factor of 4, down to
Note
You will probably come across the terminology Cp, especially when dealing with 6 sigma programs. This is the same as PCR for a centered process.
3.8.2. Uncentered processes¶
Processes are not very often centered between their upper and lower specification limits. So a measure of process capability for an uncentered processes is defined:
The
It is the Cpk value that is requested by your customer. Values of 1.3 are usually a minimum requirement, while 1.67 and higher are requested for health and safety-critical applications. A value of Cpk
You can calculate that a shift of
Note
It must be emphasized that Cpk and Cp numbers are only useful for a process which is stable. Furthermore the assumption of normally distributed samples is also required to interpret the Cpk value.