6.7.2. A conceptual explanation of PLS¶
Now that you are comfortable with the concept of a latent variable using PCA and PCR, you can interpret PLS as a latent variable model, but one that has a different objective function. In PCA the objective function was to calculate each latent variable so that it best explains the available variance in
In PLS, we also find these latent variables, but we find them so they best explain
In other words, there are three simultaneous objectives with PLS:
The best explanation of the
-space. The best explanation of the
-space. The greatest relationship between the
- and -space.
6.7.3. A mathematical/statistical interpretation of PLS¶
We will get back to the mathematical details later on, but we will consider our conceptual explanation above in terms of mathematical symbols.
In PCA, the objective was to best explain
The above was shown to be a concise mathematical way to state that these scores and loadings best explain
For PCA, for the
Now let’s look at PLS. Earlier we said that PLS extracts a single set of scores,
The objective of PLS is to extract these scores so that they have maximal covariance. Let’s take a look at this. Covariance was shown to be:
Using the fact that these scores have mean of zero, the covariance is proportional (with a constant scaling factor of
Now covariance is a hard number to interpret; about all we can say with a covariance number is that the larger it is, the greater the relationship, or correlation, between two vectors. So it is actually more informative to rewrite covariance in terms of correlations and variances:
As this shows then, maximizing the covariance between
The best explanation of the
-space: given by The best explanation of the
-space. given by The greatest relationship between the
- and -space: given by
These scores,
The above is a description of one variant of PLS, known as SIMPLS (simple PLS).
6.7.4. A geometric interpretation of PLS¶
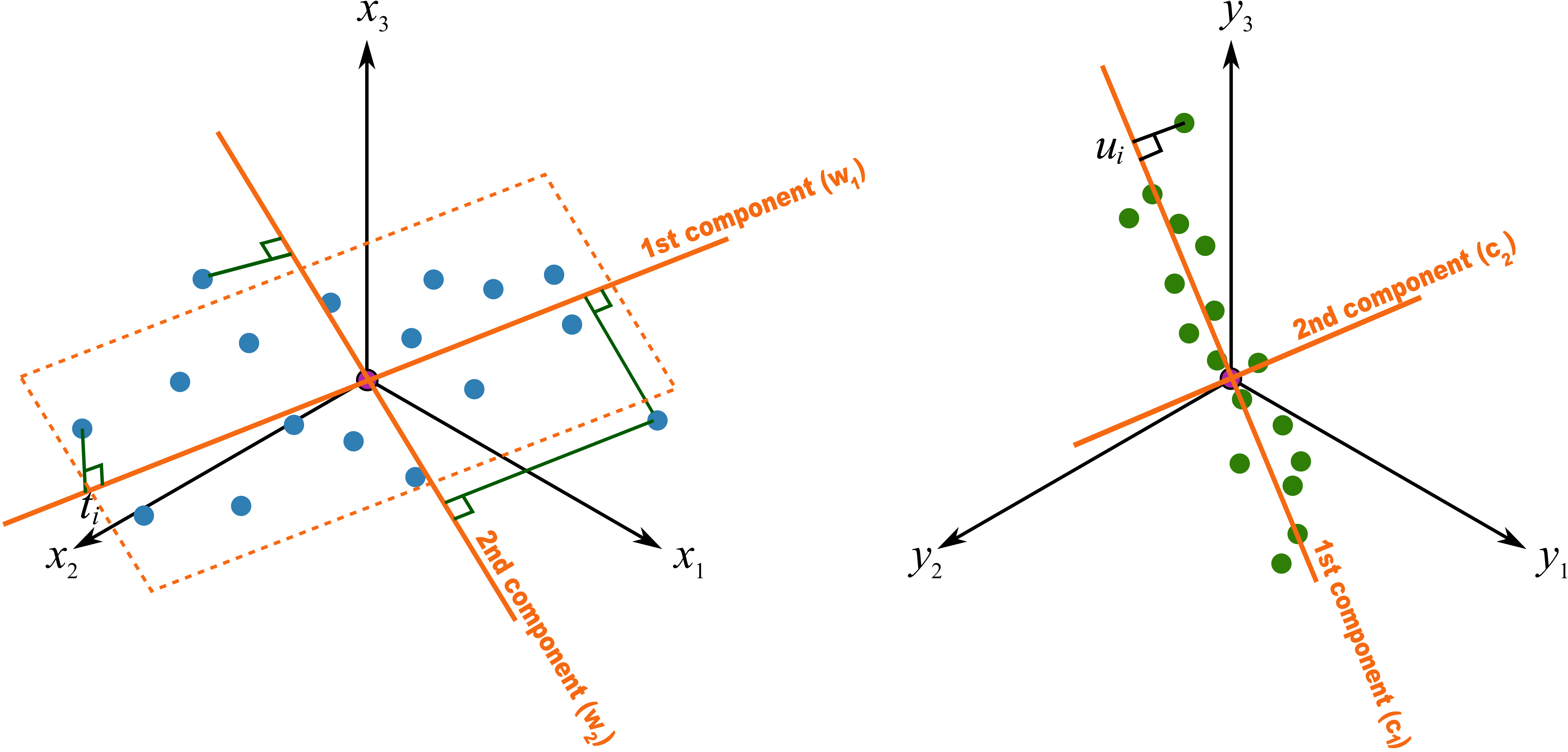
As we did with PCA, let’s take a geometric look at the PLS model space. In the illustration below we happen to have
We assume here that you understand how the scores are the perpendicular projection of each data point onto each direction vector (if not, please review the relevant section in the PCA notes). In PLS though, the direction vectors,
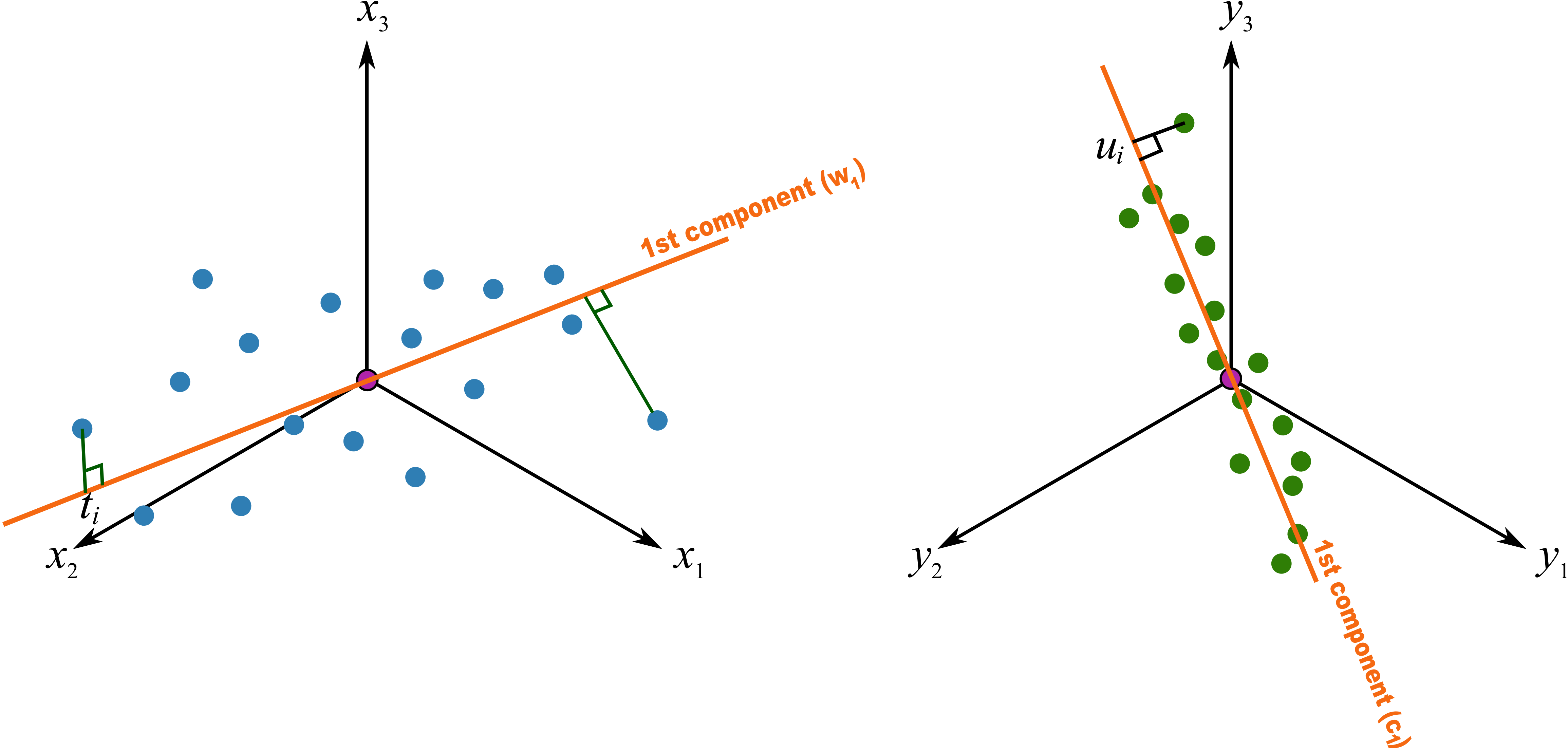
As explained above, this means that the latent variable directions are oriented so that they best explain
The second component is then found so that it is orthogonal to the first component in the