2.6. Binary (Bernoulli) distribution¶
Systems that have binary outcomes (pass/fail; yes/no) must obey the probability principle that:
An example: a histogram for a system that produces 70% acceptable product,
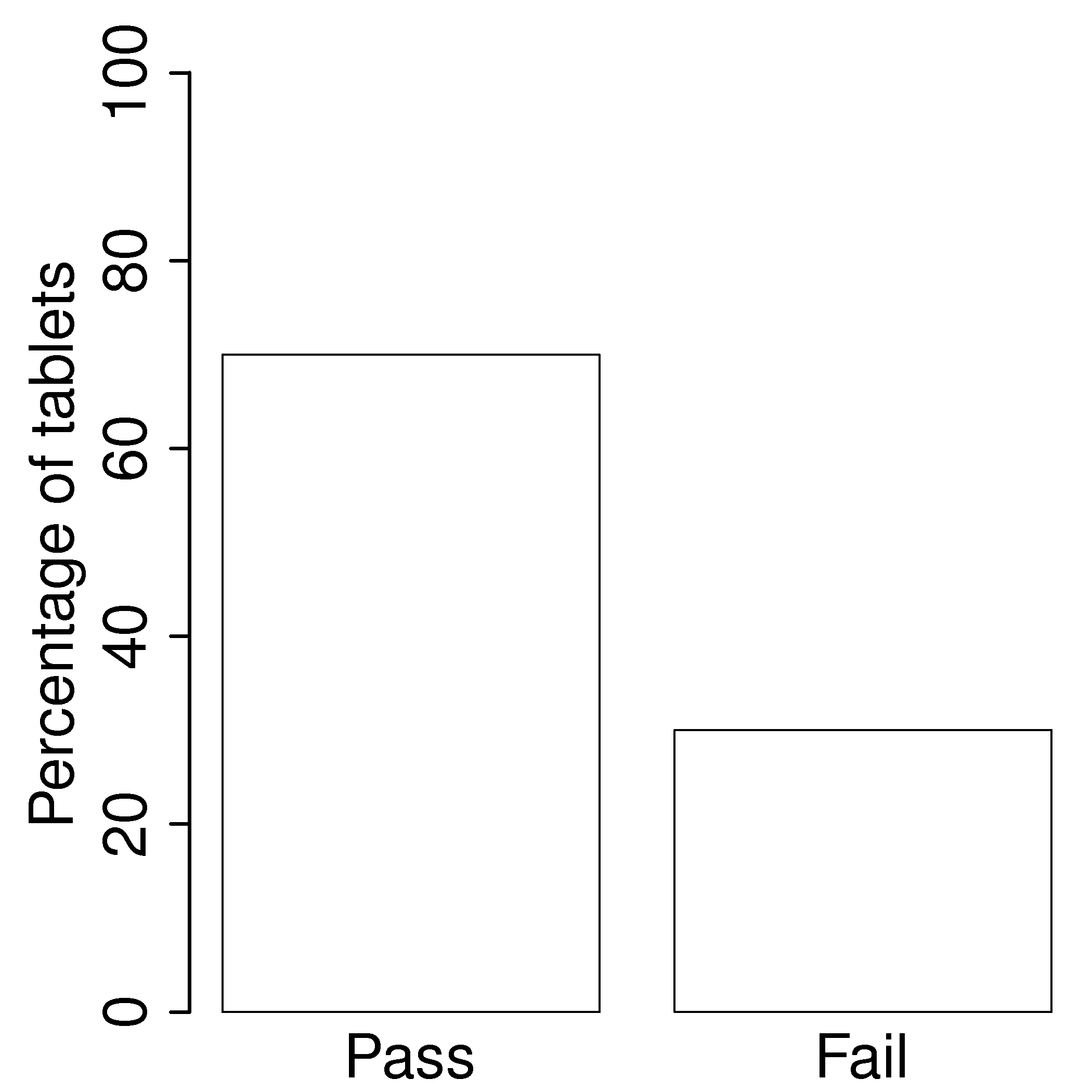
If each observation is independent of the other, then:
For the above system where
, what is probability of seeing the following sequential outcomes: pass, pass, pass (3 times in a row)?
, about one third What is the probability of seeing the sequence: pass, fail, pass, fail, pass, fail?
, less than 1%
Another example: you work in a company that produces tablets. The machine creates acceptable, unbroken tablets 97% of the time, so
In a future batch of 850,000 tablets, how many tablets are expected to be defective? (Most companies will call this quantity “the cost of waste”.)
tablets per batch will be defective You take a random sample of
tablets from a large population of tablets. What is the chance that all tablets are acceptable if is the Bernoulli population parameter of finding acceptable tablets:
Sample size
= 95%
= 97%
Are you surprised by the large reduction in the number of defective tablets for only a small increase in
? It is for this reason that a well-performing process producing accetable product does not need to have inspection of every product produced.