6.5.6. Interpreting score plots¶
Before summarizing some points about how to interpret a score plot, let’s quickly repeat what a score value is. There is one score value for each observation (row) in the data set, so there are are
The score value for an observation, for say the first component, is the distance from the origin, along the direction (loading vector) of the first component, up to the point where that observation projects onto the direction vector. We repeat an earlier figure here, which shows the projected values for 2 of the observations.
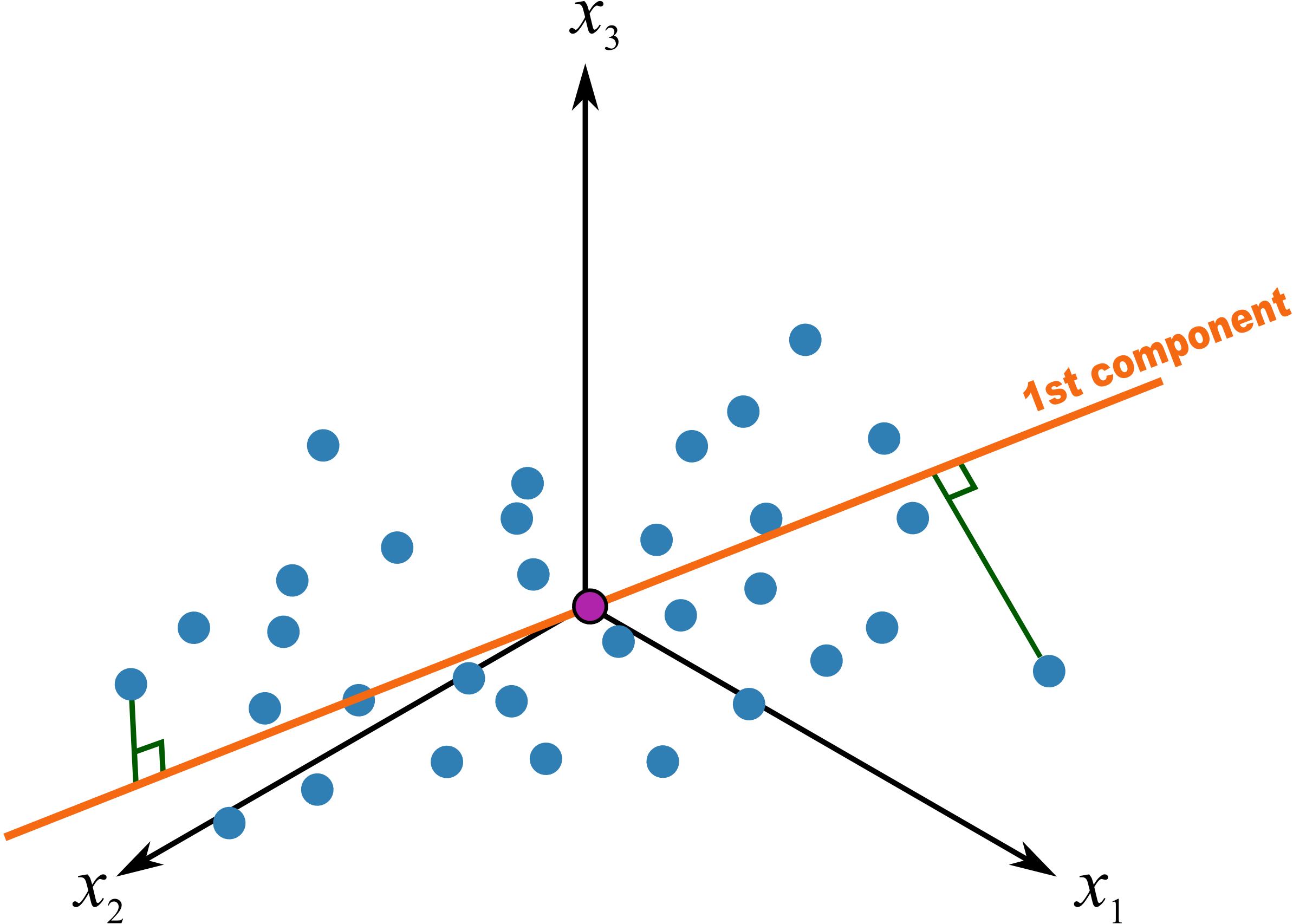
We used geometric concepts in another section that showed we can write:
The first score vector,
time-series plots of the scores, or sequence order plots, depending on how the rows of
are ordered scatter plots of one score against another score
An important point with PCA is that because the matrix
When investigating score plots we look for clustering, outliers, time-based patterns. We can also colour-code our plots to be more informative. Let’s take a look at each of these.
Clustering
We usually start by looking at the
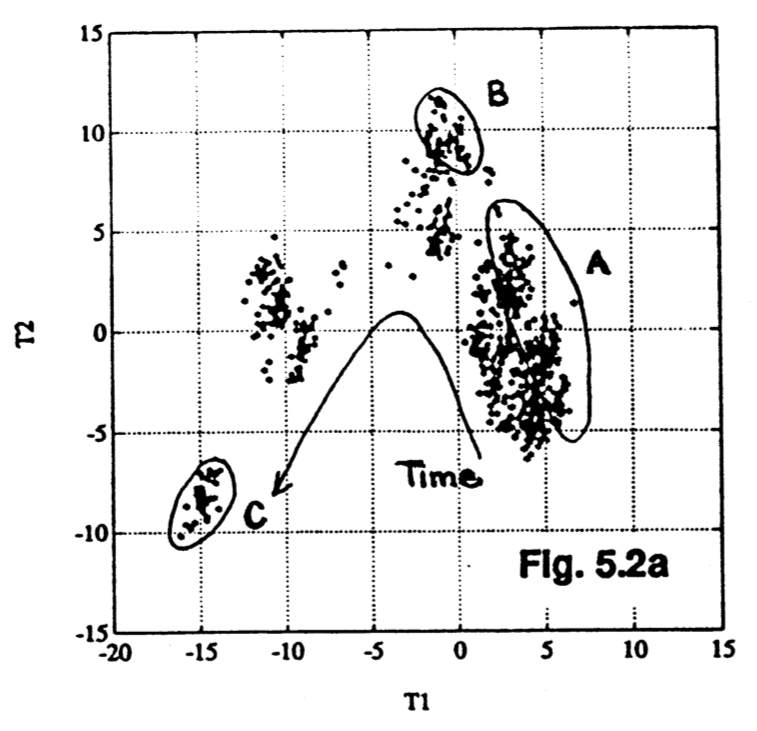
It shows how the process was operating in region A, then moved to region B and finally region C. This provides a 2-dimensional window into the movements from the
Outliers
Outliers are readily detected in a score plot, and using the equation below we can see why. Recall that the data in
Sometimes all it takes is for one variable,
But usually it is a combination of more than one
As an example from the food texture data from earlier, we saw that observation 33 had a large negative
The
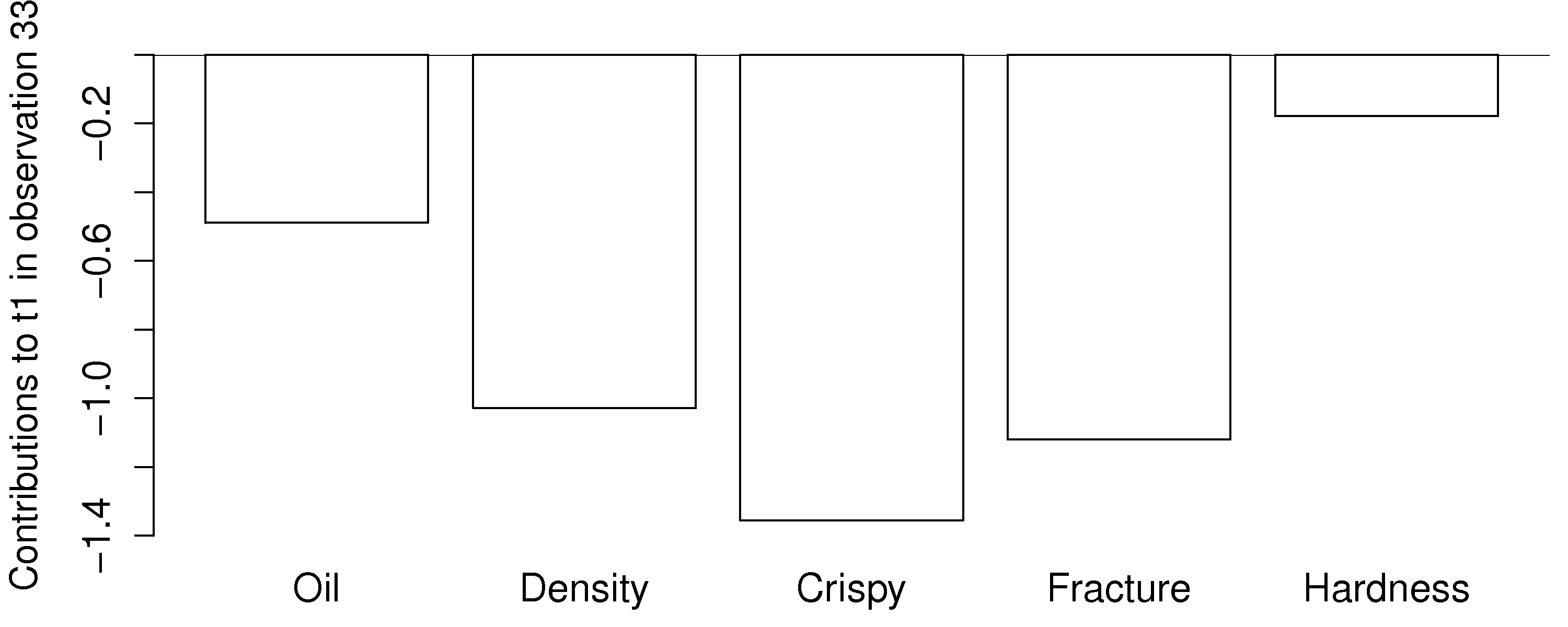
This gives a more accurate indication of exactly how the low
In the figure from the FCC process (in the preceding subsection on clustering), the cluster marked C was far from the origin, relative to the other observations. This indicates problematic process behaviour around that time. Normal process operation is expected to be in the center of the score plot. These outlying observations can be investigated as to why they are unusual by constructing contribution bar plots for a few of the points in cluster C.
Time-based or sequence-based trends
Any strong and consistent time-based or sequence-order trends in the raw data will be reflected in the scores also. Visual observation of each score vector may show interesting phenomena such as oscillations, spikes or other patterns of interest. As just described, contribution plots can be used to see which of the original variables in
Colour-coding
Plotting any two score variables on a scatter plot provides good insight into the relationship between those independent variables. Additional information can be provided by colour-coding the points on the plot by some other, 3rd variable of interest. For example, a binary colour scheme could denote success of failure of each observation.
A continuous 3rd variable can be implied using a varying colour scheme, going from reds to oranges to yellows to greens and then blue, together with an accompanying legend. For example profitability of operation at that point, or some other process variable. A 4th dimension could be inferred by plotting smaller or larger points. We saw an example of these high-density visualizations earlier.
Summary
Points close the average appear at the origin of the score plot.
Scores further out are either outliers or naturally extreme observations.
We can infer, in general, why a point is at the outer edge of a score plot by cross-referencing with the loadings. This is because the scores are a linear combination of the data in
We can determine exactly why a point is at the outer edge of a score plot by constructing a contribution plot to see which of the original variables in
Original observations in
6.5.7. Interpreting loading plots¶
Recall that the loadings plot is a plot of the direction vectors that define the model. Returning back to a previous illustration:
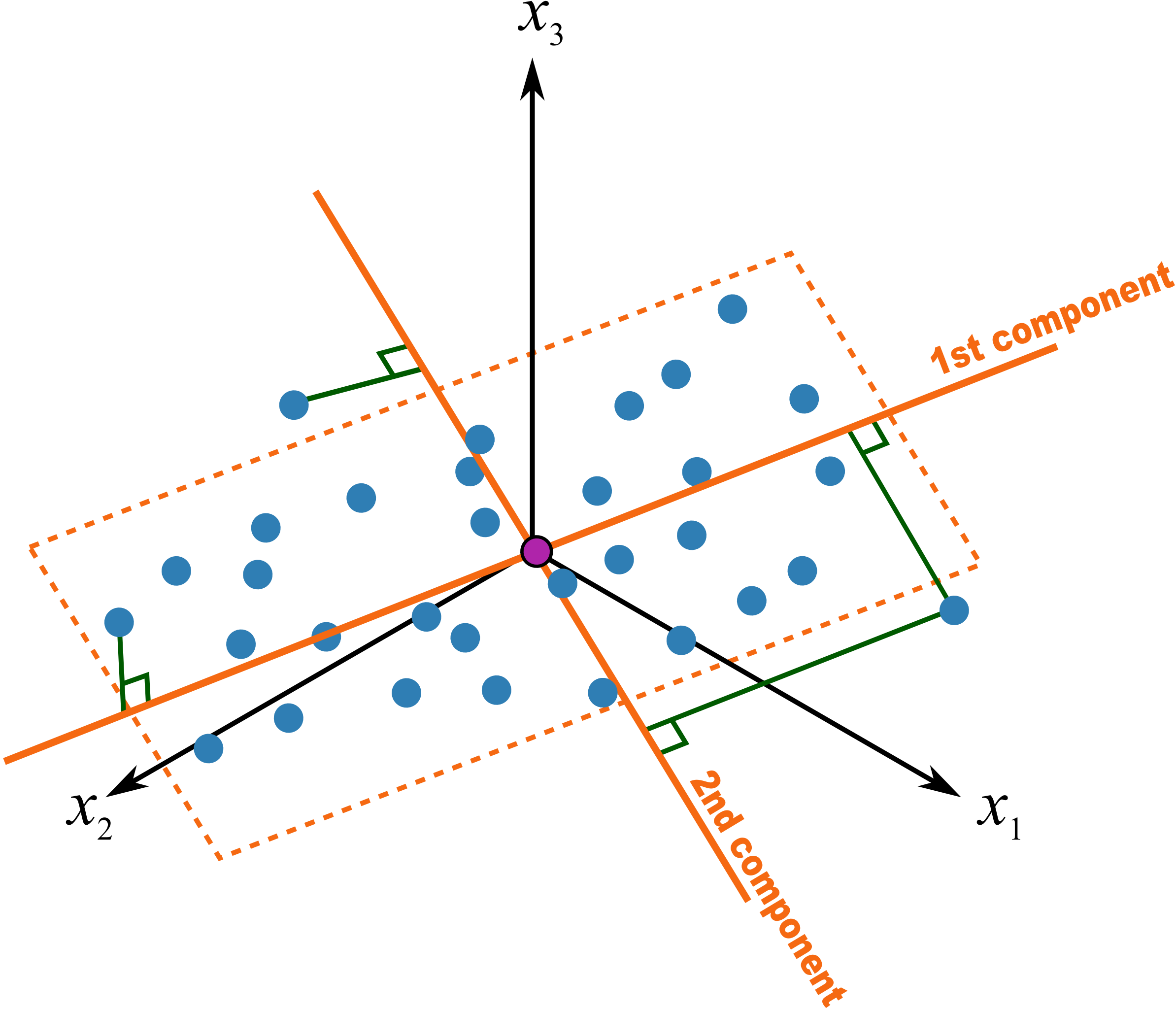
In this system the first component,
Let’s consider another visual example where two variables,
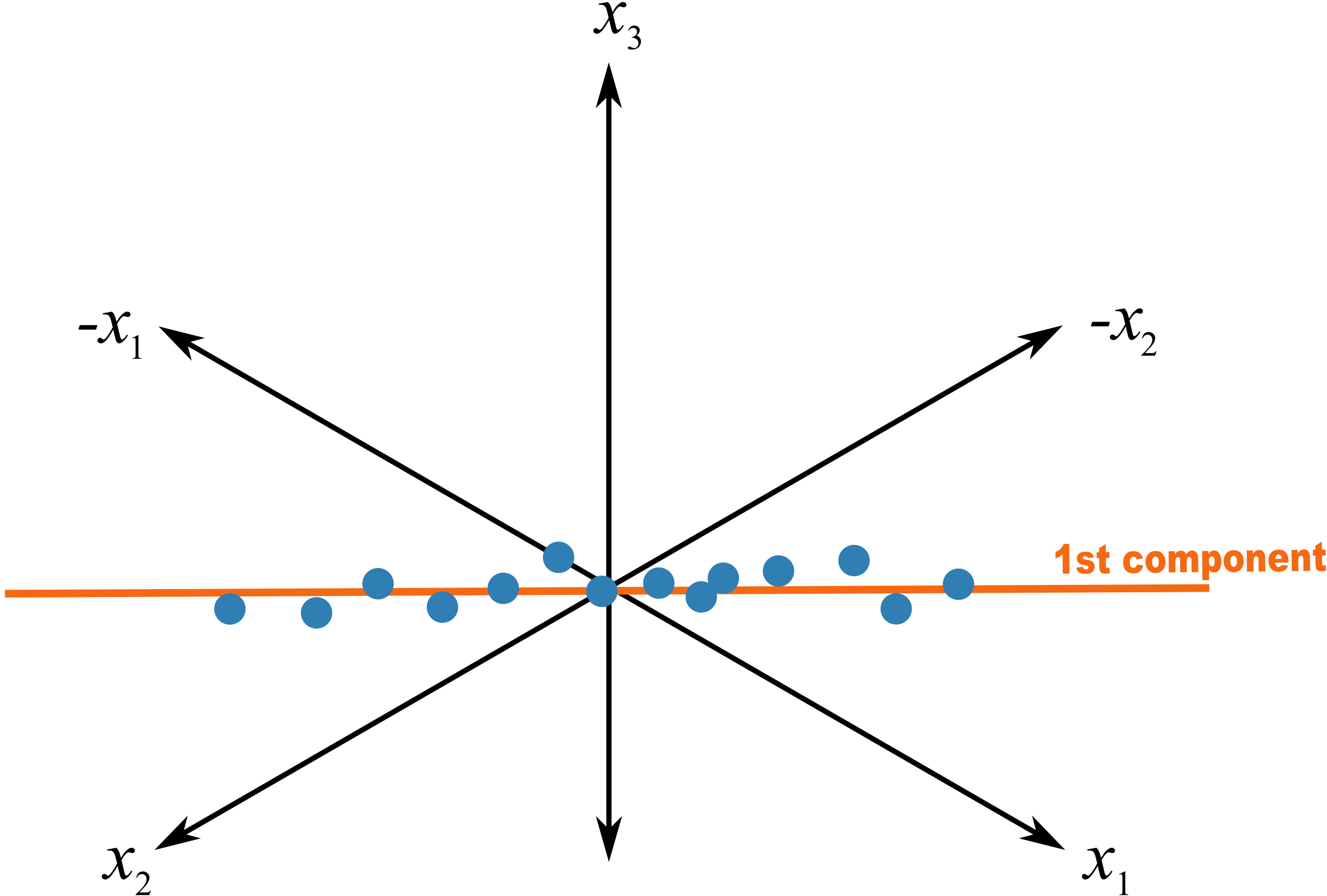
A model of such a system would have a loading vector with roughly equal weight in the
This illustrates two points:
Variables which have little contribution to a direction have almost zero weight in that loading.
Strongly correlated variables, will have approximately the same weight value when they are positively correlated. In a loadings plot of
vs they will appear near each other, while negatively correlated variables will appear diagonally opposite each other. Signs of the loading variables are useful to compare within a direction vector; but these vectors can be rotated by 180° and still have the same interpretation.
This is why they are called loadings: they show how the original variables load, (contribute), to creating the component.
Another issue to consider is the case when one has many highly correlated variables. Consider the room temperature example where the four temperatures are highly correlated with each other. The first component from the PCA model is shown here:
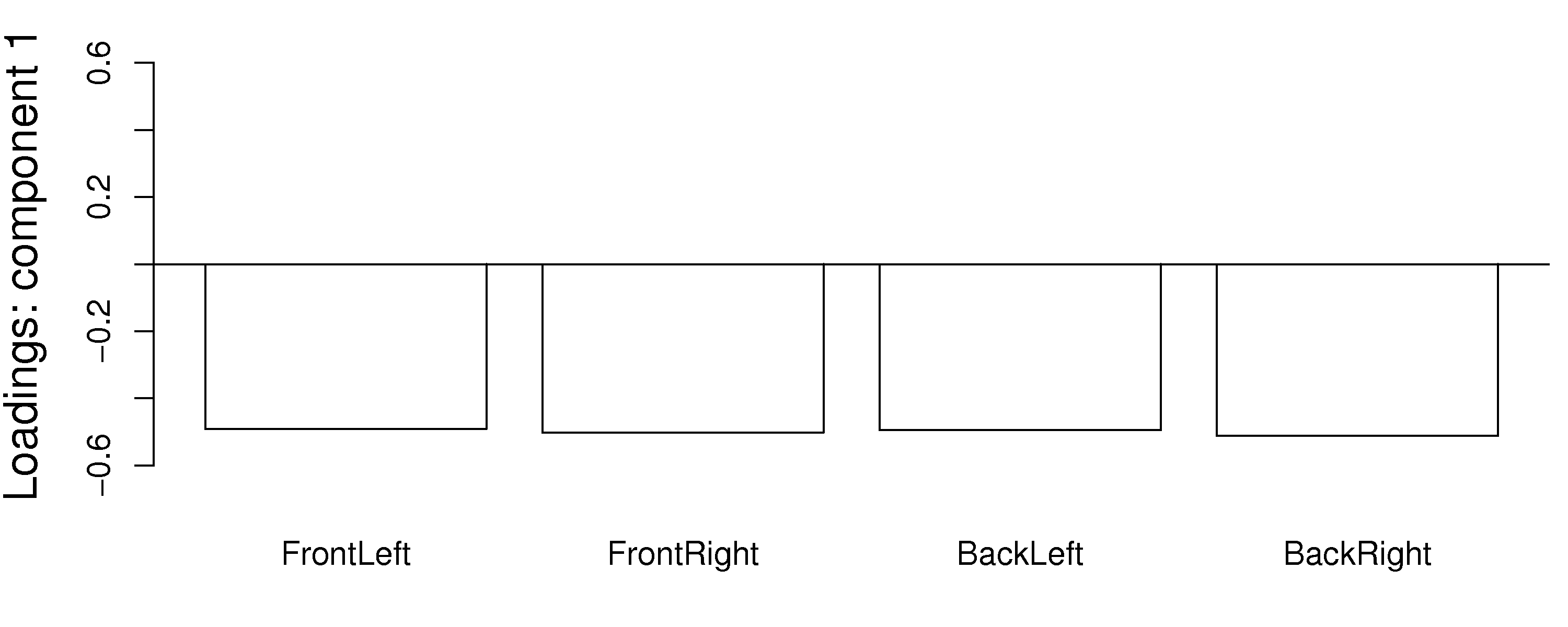
Notice how the model spreads the weights out evenly over all the correlated variables. Each variable is individually important. The model could well have assigned a weight of 1.0 to one of the variables and 0.0 to the others. This is a common feature in latent variable models: variables which have roughly equal influence on defining a direction are correlated with each other and will have roughly equal numeric weights.
Finally, one way to locate unimportant variables in the model is by finding which variables have small weights in all components. These variables can generally be removed, as they show no correlation to any of the components or with other variables.
6.5.8. Interpreting loadings and scores together¶
It is helpful to visualize any two score vectors, e.g.
Any two loadings can also be shown in a scatterplot and interpreted by recalling that each loading direction is orthogonal and independent of the other direction.
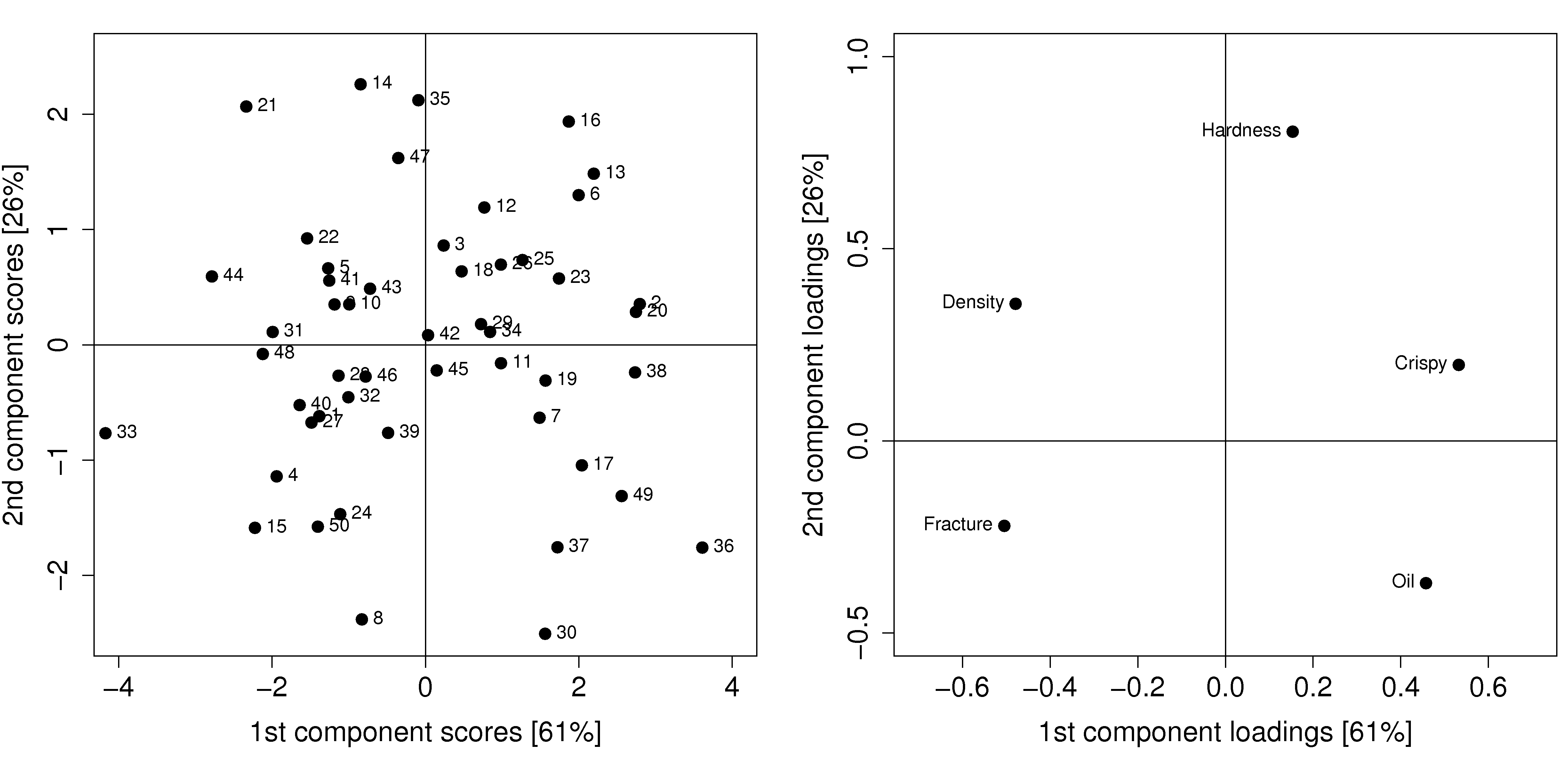
Side-by-side, these 2 plots very helpfully characterize all the observations in the data set. Recall observation 33 had a large, negative
It is no coincidence that we can mentally superimpose these two plots and come to exactly the same conclusions, using only the plots. This result comes from the fact that the scores (left) are just a linear combination of the raw data, with weighting given by the loadings (right).
Use these two plots to characterize what values the 5 measurements would have been for these observations:
sample 8:
sample 20:
sample 35:
sample 42: