6.6. Principal Component Regression (PCR)¶
Principal component regression (PCR) is an alternative to multiple linear regression (MLR) and has many advantages over MLR.
In multiple linear regression we have two matrices (blocks):
In the section on factorial experiments we intentionally set our process to generate a matrix
On most data sets though the columns in
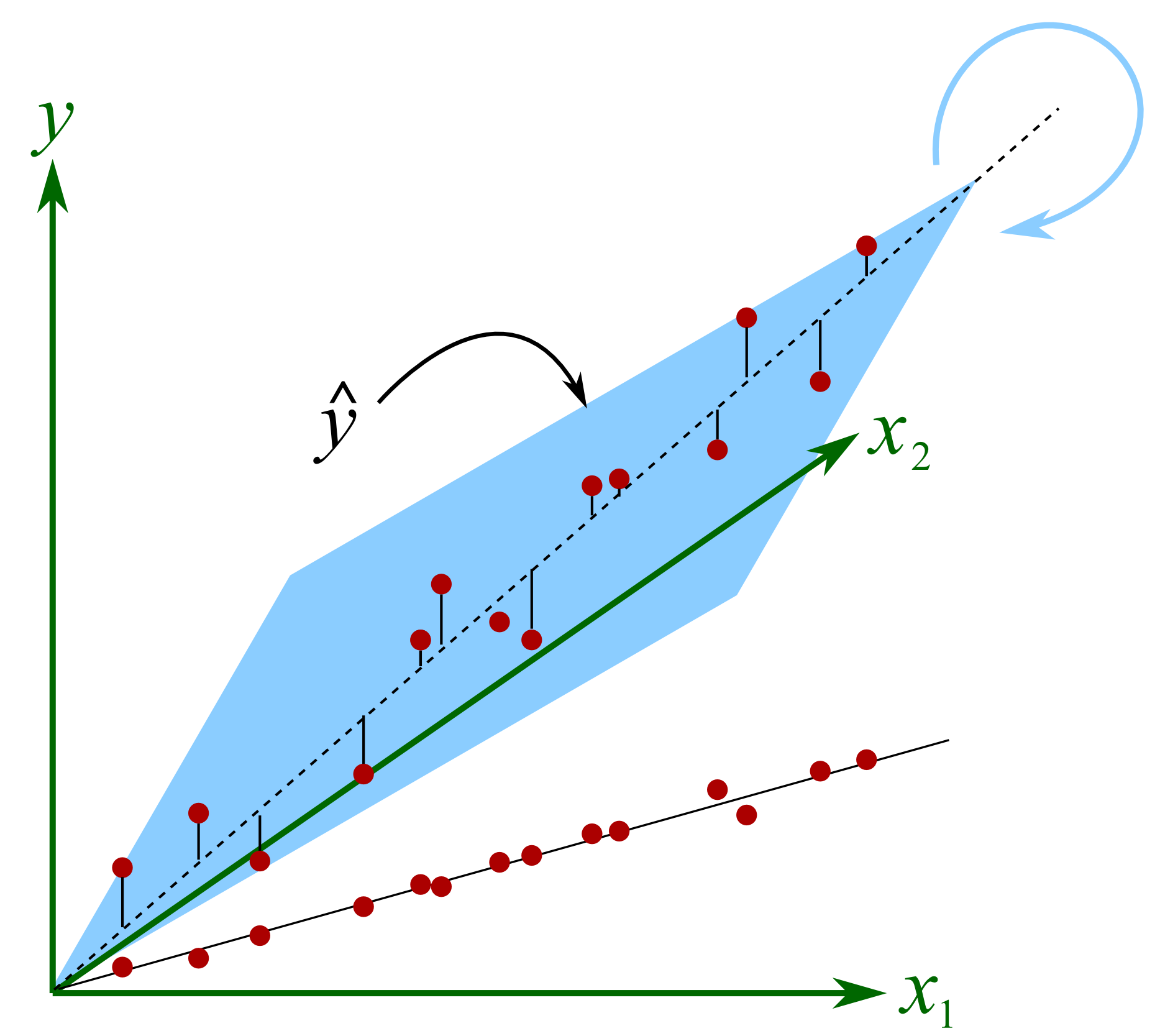
The plane will rotate around the axial, dashed line if we make small changes in the raw data. At each new rotation we will get very different values of
The common “solution” to this problem of collinearity is to revert to variable selection. In the above example the modeller would select either
We face another problem with MLR: the assumption that the variables in
it cannot handle strongly correlated columns in
it assumes
cannot handle missing values in
MLR requires that
variable selection to meet the
The main idea with principal component regression is to replace the

In other words, we replace the
This has a number of advantages:
The columns in
These
We have reduced the assumption of errors in
The relationship of each score column in
Using MLR requires that
There is much less need to resort to selecting variables from
But by far one of the greatest advantages of PCR though is the free consistency check that one gets on the raw data, which you don’t have for MLR. Always check the SPE and Hotelling’s
Illustrated as follows we see the misleading strategy that is regularly seen with MLR. The modeller has build a least squares model relating
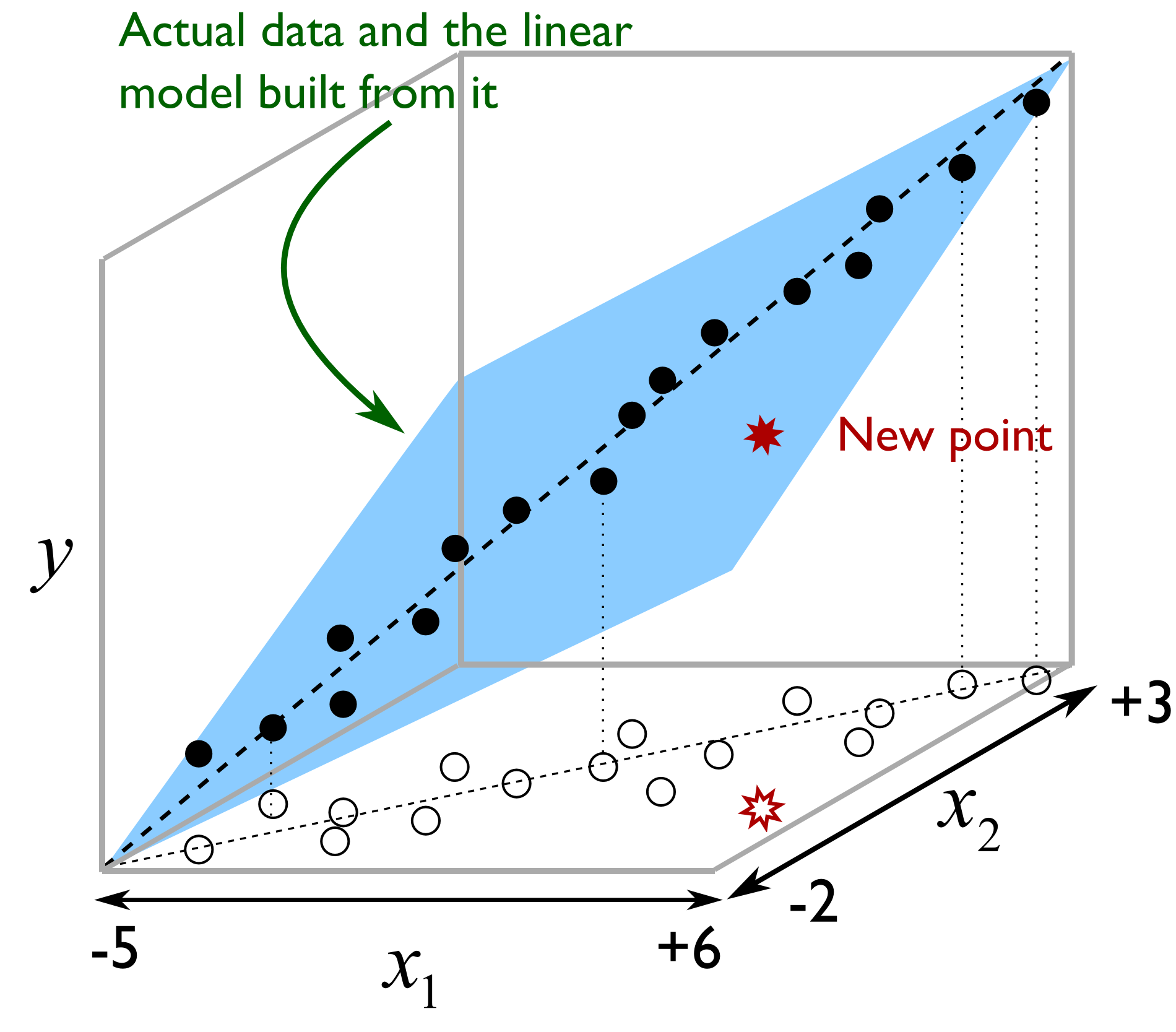
But the misleading strategy often used by engineers is to say that the model is valid as long as
Here then is the procedure for building a principal component regression model.
Collect the
Build a PCA model on the data in
Examine the SPE and
Use the columns in
Solve for the MLR model parameters,
Using the principal component regression model for a new observation:
Obtain your vector of new data,
Preprocess this vector in the same way that was done when building the PCA model (usually just mean centering and scaling) to obtain
Calculate the scores for this new observation:
Find the predicted value of this observation:
Calculate the residual vector:
Then compute the residual distance from the model plane:
And the Hotelling’s
Before calculating the prediction from the PCR model, first check if the
If either of the
Predictions of
Multiple linear regression, though relatively simpler to implement, has no such consistency check on the new observation’s
One of the main applications in engineering for PCR is in the use of software sensors, also called inferential sensors. The method of PLS has some distinct advantages over PCR, so we prefer to use that method instead, as described next.