6.7.11. PLS Exercises¶
6.7.11.1. The taste of cheddar cheese¶
Description: This very simple case study considers the taste of mature cheddar cheese. There are 3 measurements taken on each cheese: lactic acid, acetic acid and
Import the data into R:
cheese <- read.csv('http://openmv.net/file/cheddar-cheese.csv')Use the
carlibrary and plot a scatter plot matrix of the raw data:library(car)scatterplotMatrix(cheese[,2:5])
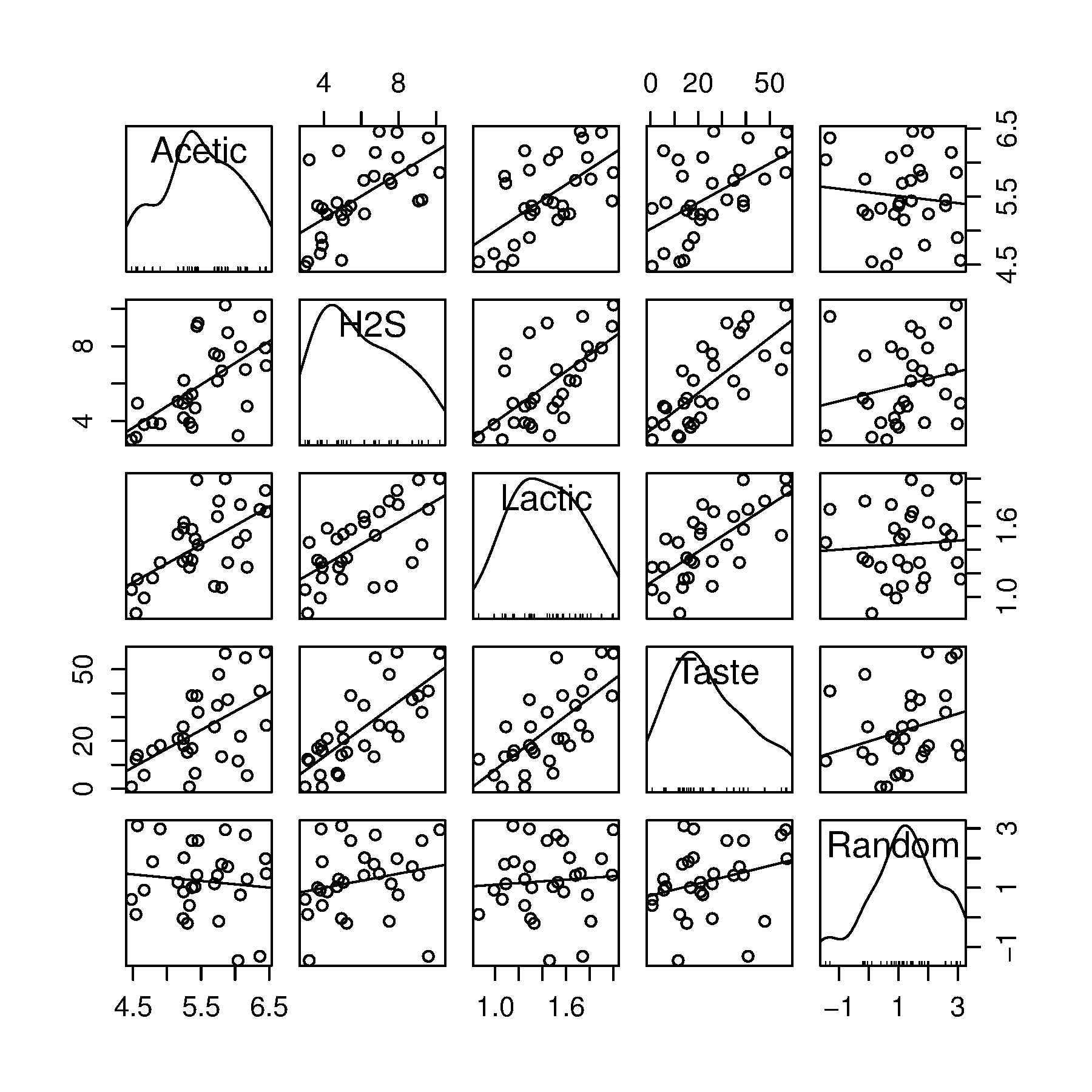
Using this figure, how many components do you expect to have in a PCA model on the 3
Acetic,H2SandLactic?What would the loadings look like?
Build a PCA model now to verify your answers.
Before building the PLS model, how many components would you expect? And what would the weights look like (
Build a PLS model and plot the
Now plot the SPE plot; these are the SPE values for the projections onto the
In R, build a least squares model that regresses the
Tastevariable on to the other 3model.lm <- lm(Taste ~ Acetic + H2S + Lactic, data=cheese)Report each coefficient
confint(model.lm)function too.)Report the standard error and the
Compare this to the PLS model’s
Now build a PCR model in R using only 1 component, then using 2 components. Again calculate the standard error and
Plot the observed
PLS models do not have a standard error, since the degrees of freedom are not as easily defined. But you can calculate the RMSEE (root mean square error of estimation) =
Obviously the best way to test the model is to retain a certain amount of testing data (e.g. 10 observations), then calculate the root mean square error of prediction (RMSEP) on those testing data.
6.7.11.2. Comparing the loadings from a PCA model to a PLS model¶
PLS explains both the
The data are from the plastic pellets troubleshooting example.
Description: 3 of the 6 measurements are size values for the plastic pellets, while the other 3 are the outputs from thermogravimetric analysis (TGA), differential scanning calorimetry (DSC) and thermomechanical analysis (TMA), measured in a laboratory. These 6 measurements are thought to adequately characterize the raw material. Also provided is a designation
AdequateorPoorthat reflects the process engineer’s opinion of the yield from that lot of materials.
Build a PCA model on all seven variables, including the 0-1 process outcome variable in the
How do the loadings look for the first, second and third components?
Now build a PLS model, where the
How many components were required by cross-validation for the PLS model?
Explain why the PLS loadings are different to the PCA loadings.
6.7.11.3. Predicting final quality from on-line process data: LDPE system¶
Link to dataset website and description of the data.
Build a PCA model on the 14
Build a PCA model on the 5
Conv,Mn,Mw,LCB, andSCB. Use only the first 50 observationsBuild a PLS model relating the
Compare the loadings plot from PCA on the
What is the
Now let’s look at the interpretation between the
Which variable(s) in
Conv)? In other words, as an engineer, which of the 14Would these adjustments affect any other quality variables? How would they affect the other quality variables?
How would you adjust the quality variable called
Mw(the weight average molecular weight)?