3.5. CUSUM charts¶
We showed earlier that the Shewhart chart is not too sensitive to detecting shifts in the mean. Depending on the subgroup size,
The following equation shows how this chart works.
Values of
So imagine a CUSUM chart where at some time point the process mean shifts up by
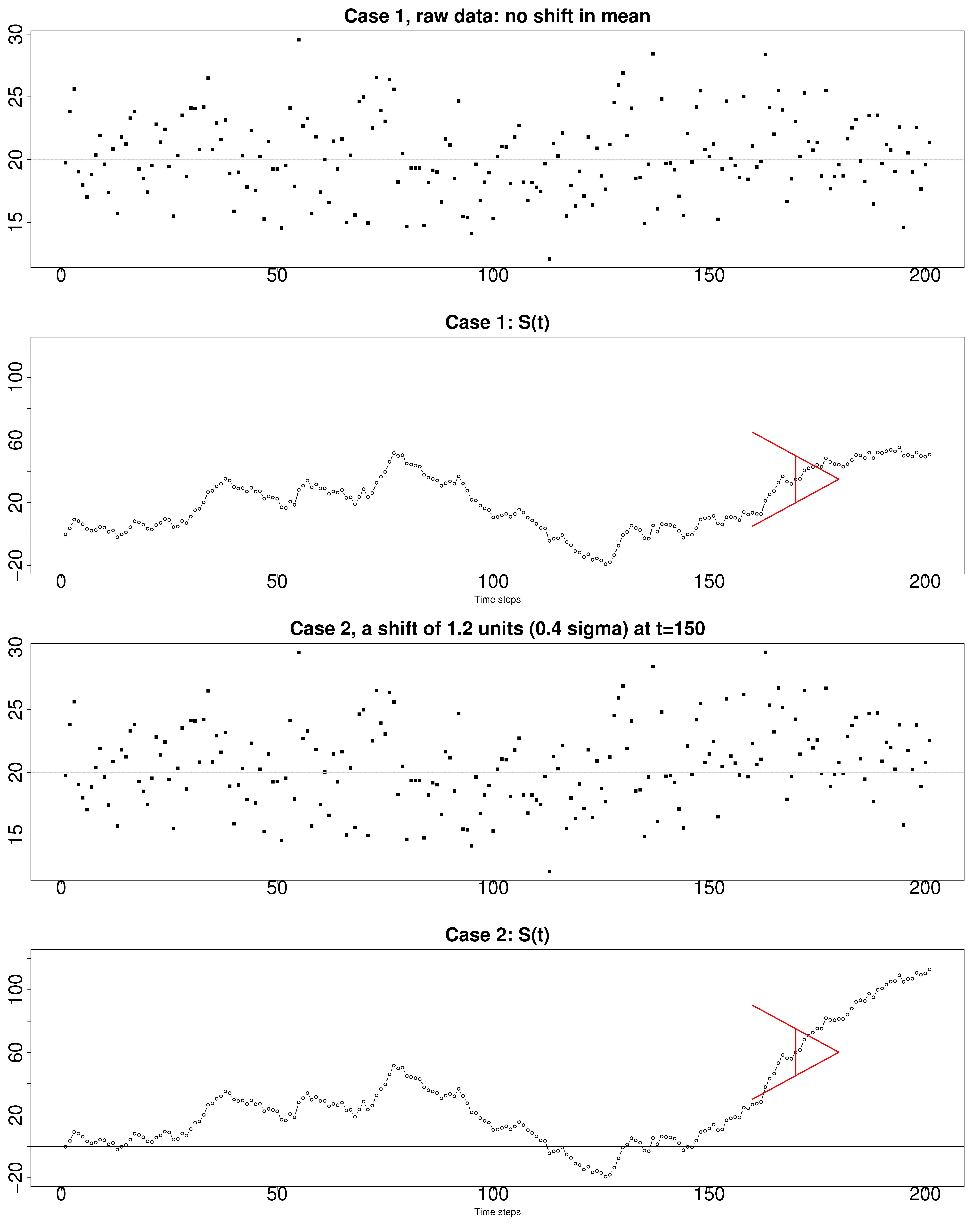
The CUSUM chart is extremely sensitive to small changes. The example chart is shown here for a process where the mean is
This figure also shows how the CUSUM chart is used with the 2 masks. Notice that there are no lower and upper bounds for
What is of interest however is a persistent change in slope in the CUSUM chart. The angle of the superimposed V-mask is the control limit: the narrower the mouth of the mask, the more sensitive the CUSUM chart is to deviations from the target. Both the type I and II error are set by the angle of the V and the leading distance (the distance from the short vertical line to the apex of the V).
The process is considered in control as long as all points are within the arms of the V shape. The mask in the second row of the plot shows “in control” behaviour, while the mask in the fourth row detects the process mean has shifted, and an alarm should be raised.
Once the process has been investigated the CUSUM value,
The purpose of this section is not to provide formulas for the V-mask or tabular CUSUM charts, only to explain the CUSUM concept to put the next section on EWMA control charts in perspective.