2.10. Poisson distribution¶
The Poisson distribution is useful to characterize rare events (number of cell divisions in a small time unit), system failures and breakdowns, or number of flaws on a product (contaminations per cubic millimetre). These are events that have a very small probability of occurring within a given time interval or unit area (e.g. pump failure probability per minute = 0.000002), but there are many opportunities for the event to possibly occur (e.g. the pump runs continuously). A key assumption is that the events must be independent. If one pump breaks down, then the other pumps must not be affected; if one flaw is produced per unit area of the product, then other flaws that appear on the product must be independent of the first flaw.
Let
There are two important properties:
The mean of the distribution for the rate happens to be the rate at which unusual events occur =
The variance of the distribution is also
Formally, the Poisson distribution can be written as
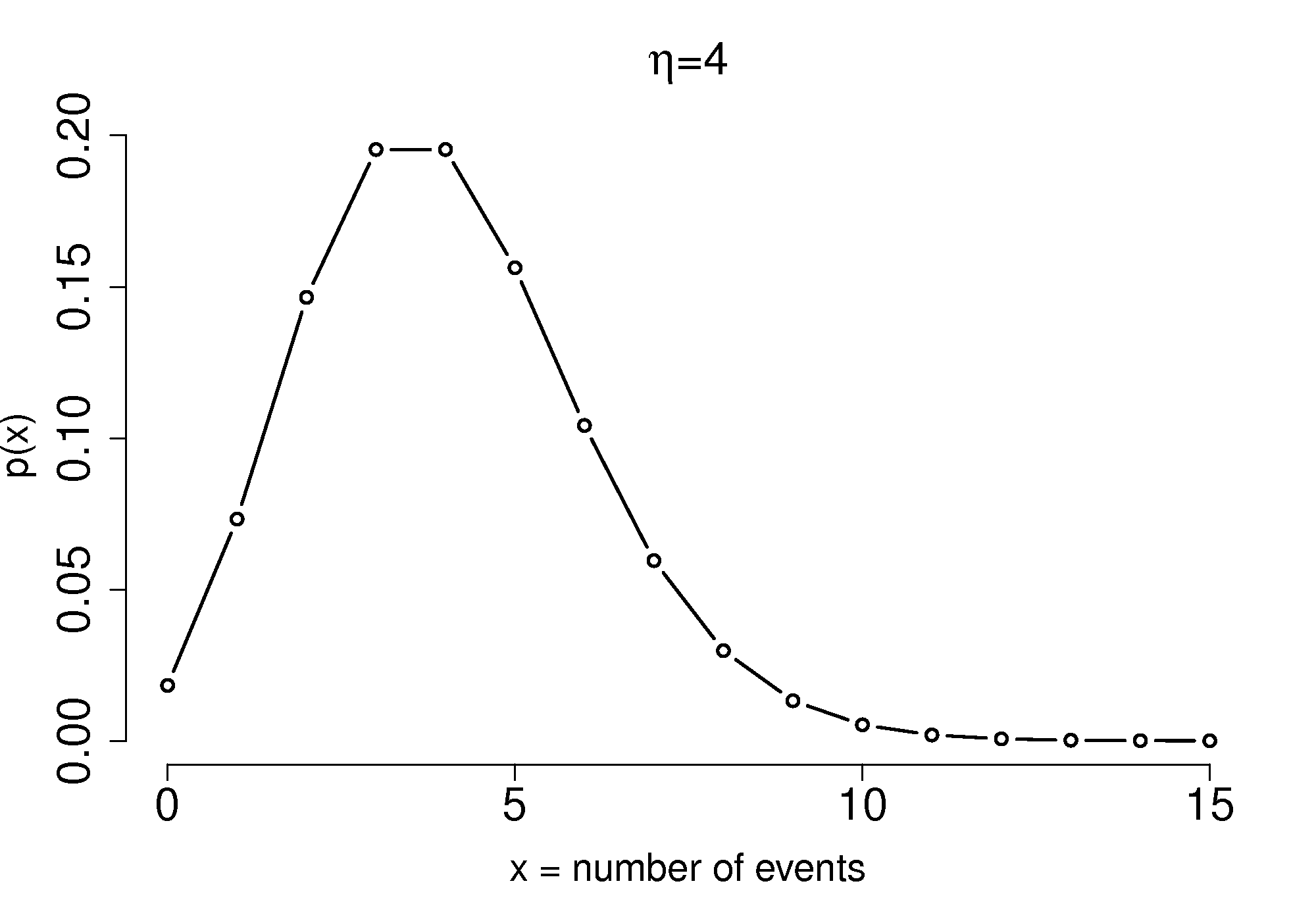
Example: Equipment in a chemical plant can and will fail. Since it is a rare event, let’s use the Poisson distribution to model the failure rates. Historical records on a plant show that a particular supplier’s pumps are, on average, prone to failure in a month with probability
0
0.25% chance
1
1.5%
3
8.9
6
16%
10
4.1%
15
0.1%