3.12. Exercises

Question

Is it fair to say that a monitoring chart is like an online version of a confidence interval? Explain your answer.

Solution

This question is likely to generate a wide range of answers. No surprise, since there are strong feelings on this point in the quality control literature as well. The confusion stems from the fact that if you are in phase 1, then no, a monitoring chart is not a confidence interval, but in phase 2, then you can argue that confidence intervals have many similarities to monitoring charts.

But, in general, I feel the above statement is incorrect. Even in phase 2 a monitoring chart is not really like an on-line confidence interval. Mainly because a monitoring chart is intended to check for system stability, and to alarm quickly if the system moves away from the assumed distribution (usually a normal distribution). The monitoring limits are calculated to provide the required alarm level (the ARL). A confidence interval, on the other hand, defines the limits within which we expect to find the true population mean with a certain degree of confidence when we use a given sample of data.

The similarity comes from the way the monitoring chart’s limits are calculated: by using the concept of a confidence interval. But a monitoring chart’s limits can and should be adjusted up or down to improve your type I and II error levels, while for a confidence interval, the only way to alter the limits is to take a different sample size, take a new sample of data, and choose a different level of confidence. But doing this, will still only find you bounds within which you expect the population mean to lie. A monitoring chart’s bounds are only there to signal when things are not the same any more.

Question

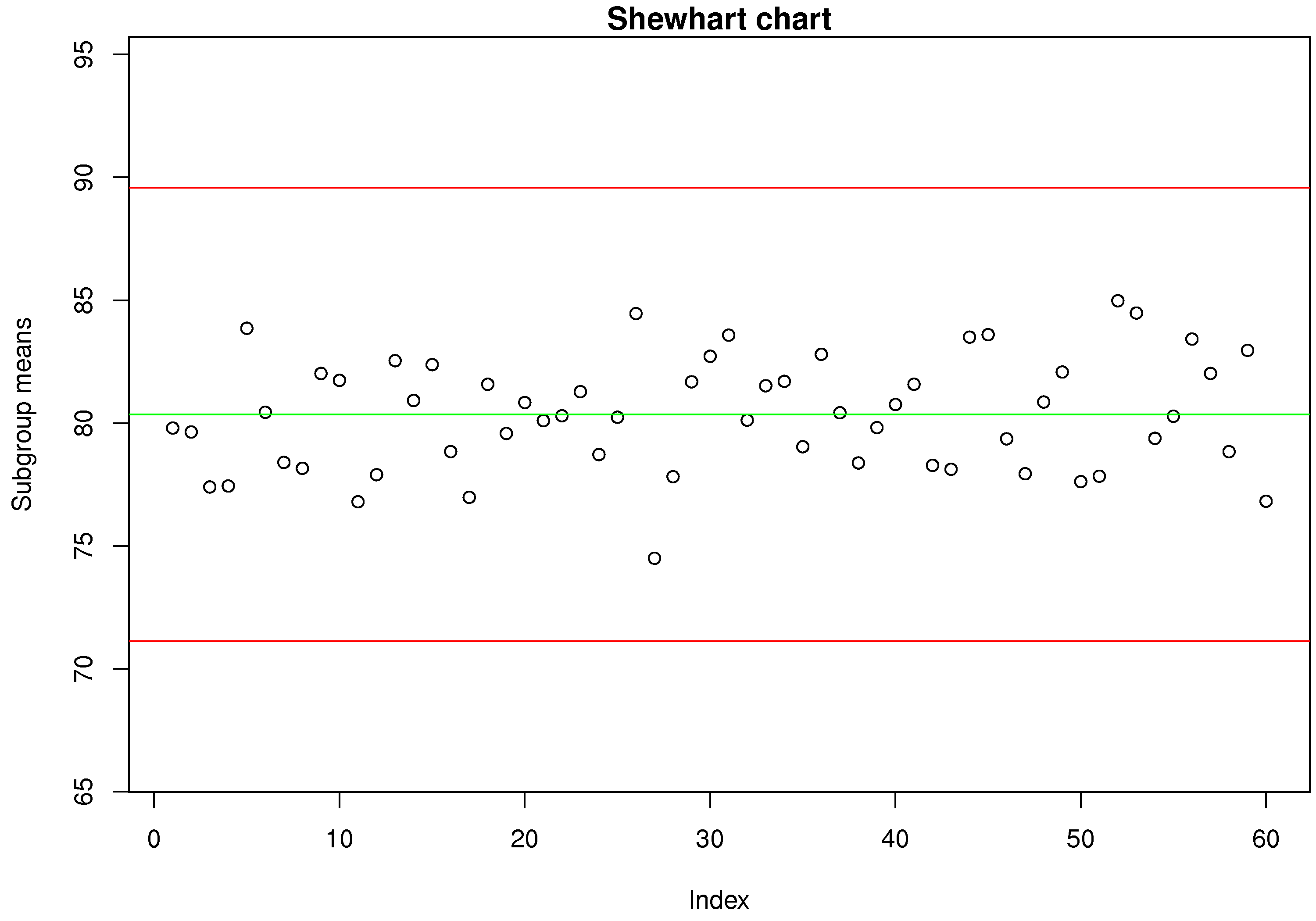
Use the batch yields data and construct a monitoring chart using the 300 yield values. Use a subgroup of size 5. Report your target value, lower control limit and upper control limit, showing the calculations you made. I recommend that you write your code so that you can reuse it for other questions.

Solution

Please see the code below. The Shewhart chart’s parameters are as below, with plots generated from the R code.

• Target = 80.4

• Lower control limit at 3 standard deviations = 71.1

• Upper control limit at 3 standard deviations = 89.6

Try it yourself:

Python, 58 lines

import numpy as np
import pandas as pd
from scipy.special import gamma

pd.options.plotting.backend = "plotly"

data_file = "https://openmv.net/file/batch-yields.csv"
batch = pd.read_csv(data_file)

# Make sure we have the expected data.
batch.describe()
Yield = batch["Yield"].to_numpy()

# To get a feel for the data; looks pretty
# good, no unusual outliers.
pd.Series(Yield).plot.line().show()

N = len(Yield)
N_sub = 5  # subgroup size
# Reshape so each column is one subgroup.
subgroup = Yield.reshape(N // N_sub, N_sub).T
N_groups = subgroup.shape[1]
subgroup.shape  # (5, 60)

subgroup_sd = subgroup.std(axis=0, ddof=1)
subgroup_xbar = subgroup.mean(axis=0)

# Take a look at what these numbers mean.
pd.Series(subgroup_xbar).plot.line().update_layout(
    yaxis_title_text="Subgroup average").show()
pd.Series(subgroup_sd).plot.line().update_layout(
    yaxis_title_text="Subgroup spread").show()

# Report your target value, lower control
# limit and upper control limit, showing
# the calculations you made.
target = subgroup_xbar.mean()
Sbar = subgroup_sd.mean()

# a_n value is from the table when
# subgroup size = 5
an_num = np.sqrt(2) * gamma(N_sub / 2)
an_den = np.sqrt(N_sub - 1) * gamma(N_sub / 2 - 0.5)
an = an_num / an_den
sigma_estimate = Sbar / an
LCL = target - 3 * sigma_estimate / np.sqrt(N_sub)
UCL = target + 3 * sigma_estimate / np.sqrt(N_sub)
(LCL, target, UCL)

fig = pd.Series(subgroup_xbar).plot.line(
    title="Shewhart chart")
fig.update_layout(
    yaxis=dict(range=[LCL - 5, UCL + 5],
               title_text="Subgroup means"))
fig.add_hline(y=target, line_color="green")
fig.add_hline(y=UCL, line_color="red")
fig.add_hline(y=LCL, line_color="red")
fig.show()

R, 51 lines

data_file <- 'https://openmv.net/file/batch-yields.csv'
batch <- read.csv(data_file)

# make sure we have the expected data
summary(batch)
attach(batch)

# To get a feel for the data;
# looks pretty good; no unusual outliers
plot(Yield)

N = length(Yield)
N.sub = 5       # subgroup size
subgroup <- matrix(Yield, N.sub, N/N.sub)
N.groups <- ncol(subgroup)
dim(subgroup)   # 5 by 60 matrix

subgroup.sd <- apply(subgroup, 2, sd)
subgroup.xbar <- apply(subgroup, 2, mean)

# Take a look at what these numbers mean
plot(subgroup.xbar,
     type="b",
     ylab="Subgroup average")
plot(subgroup.sd,
     type="b",
     ylab="Subgroup spread")

# Report your target value, lower control
# limit and upper control limit, showing
# the calculations you made.
target <- mean(subgroup.xbar)
Sbar <- mean(subgroup.sd)

# a_n value is from the table when
# subgroup size = 5
an <- 0.94
an.num <- sqrt(2)*gamma(N.sub/2)
an.den <- sqrt(N.sub-1)*gamma(N.sub/2-0.5)
an <- an.num/an.den
sigma.estimate <- Sbar / an
LCL <- target - 3 * sigma.estimate/sqrt(N.sub)
UCL <- target + 3 * sigma.estimate/sqrt(N.sub)
c(LCL, target, UCL)
plot(subgroup.xbar,
     ylim=c(LCL-5, UCL+5),
     ylab="Subgroup means",
     main="Shewhart chart")
abline(h=target, col="green")
abline(h=UCL, col="red")
abline(h=LCL, col="red")

Question

The boards data on the website are from a line which cuts spruce, pine and fir (SPF) to produce general quality lumber that you could purchase at Rona, Home Depot, etc. The price that a saw mill receives for its lumber is strongly dependent on how accurate the cut is made. Use the data for the 2 by 6 boards (each row is one board) and develop a monitoring system using these steps.

1. Plot all the data.

2. Now assume that boards 1 to 500 are the phase 1 data; identify any boards in this subset that appear to be unusual (where the board thickness is not consistent with most of the other operation)

3. Remove those unusual boards from the phase 1 data. Calculate the Shewhart monitoring limits and show the phase 1 data with these limits. Note: choose a subgroup size of 7 boards.

4. Test the Shewhart chart on boards 501 to 2000, the phase 2 data. Show the plot and calculate the type I error rate (\(\alpha\)) from the phase 2 data; assuming, of course, that all the phase 2 data are from in-control operation.

5. Calculate the ARL and look at the chart to see if the number looks about right. Use the time information in the raw data and your ARL value to calculate how many minutes between a false alarm. Will the operators be happy with this?

6. Describe how you might calculate the consumer’s risk (\(\beta\)).

7. How would you monitor if the saws are slowly going out of alignment?

Solution

This questions answers are derived in the source code (at the end).

1. A plot of the raw data:

   

2. A plot of just the phase 1 data shows no particular outliers. Most people found a few outliers, that’s OK - remember it is a subjective test, and if this were a process you were responsible for, then you would know more clearly what an outlier was. For me though, I didn’t think any of these points were particularly unusual.

   

3. Each board carries six thickness measurements across its width; we use the median of those six values as the single thickness for that board. The initial Shewhart parameters found were:

   • UCL = 1699

   • Target = 1677

   • LCL = 1655

   When plotting these limits on the phase 1 data, there was only one subgroup that was found outside the limits (the first subgroup). This subgroup is removed and the limits recalculated. (For this case there was only one, very moderate, subgroup outside the limits - the new limits are basically the same). The new limits

   • UCL = 1698

   • Target = 1676

   • LCL = 1654

   A Shewhart chart of all the phase 1 data (including outliers, to highlight them) is shown here. The limits were the final limits, after iteratively removing the first unusual subgroup. The code contains all the calculation steps.

   

4. Using these parameters on the phase 2 data generates the following plot:

   

   Assuming the subgroups in phase 2 are all in control, the \(\alpha\) value is sum of the points outside the limits, divided by the total number of subgroups in phase 2 = 6/214 = 2.8%. This is much greater than the theoretically expected \(\alpha\) of 0.27%.

   Notice though there is a group of points all on one side of the target line. According to the Western Electric rules, a group of more than 8 points on one side of the target line is highly improbable and an alarm should be raised. This indicates that these phase 2 testing data are likely not from in-control operation.

5. The ARL = \(1/\alpha = 1/0.028\) = 35.7; i.e. 1 subgroup in every 36 will lie outside the control limits, even if that subgroup is from in-control operation. That number looks about right from the above phase 2 chart, although, most of the outliers seem to occur in the last half of the chart (see answer to part 4). The time stamps in the raw data show that boards 1 to 2000 span about 5 hours and 24 minutes (324 minutes) of operation; during this time there were 285 subgroups that would have been shown on a real Shewhart chart. With an ARL of 36 subgroups, there would be about 8 (285/36) false alarms over these 324 minutes. In other words a false alarm about once every 41 minutes. This is still too high for practical use. Either the limits must be made wider, or this data really is not from in-control operation.

6. To calculate the consumer’s risk (\(\beta\)) we require a period of data where we know the blades have shifted, so that the board thickness has been increased or decreased to a new level (mean operating point). Using that out of control, or unstable data, we calculate Shewhart subgroups as usual, and count the number of data points falling within the current LCL and UCL. A count of those in control subgroups divided by the total number of these out of control subgroups would be an estimate of \(\beta\).

7. As the blades go out of alignment, the variability in the thickness values increases. Two ways to monitor this are

   • To plot the subgroup standard deviation over time. I have added the nonparametric regression lines against time on the plot to highlight how the variability increases over time. This indicates to me that this data probably was not from in control operation. This is the reality in most processes: we are never sure that the data are from in-control operation; it is always trial and error.

   • Use a CUSUM chart.

   • A more sensitive monitoring chart for this would be the exponentially weighted moving variance: MacGregor, J.F. and Harris, T.J., “The Exponentially Weighted Moving Variance”, Journal of Quality Technology, 25, p 106-118, 1993.

   

The calculation steps, in Python:

Python, 55 lines

import numpy as np
import pandas as pd
from scipy.special import gamma

pd.options.plotting.backend = "plotly"

file = "https://openmv.net/file/six-point-board-thickness.csv"
boards = pd.read_csv(file)

# One thickness per board: the median of the six positions.
positions = ["Pos1", "Pos2", "Pos3", "Pos4", "Pos5", "Pos6"]
thickness = boards[positions].median(axis=1).to_numpy()

N_sub = 7                    # subgroup size (7 boards)
phase1_end = 500 // N_sub    # boards 1-500  -> 71 subgroups
phase2_end = 2000 // N_sub   # boards 1-2000 -> 285 subgroups

def an(n):
    return (np.sqrt(2) * gamma(n / 2)
            / (np.sqrt(n - 1) * gamma((n - 1) / 2)))

# Subgroup means and standard deviations (7 consecutive boards).
g = thickness[: (len(thickness) // N_sub) * N_sub].reshape(-1, N_sub).T
xbar, S = g.mean(axis=0), g.std(axis=0, ddof=1)

def limits(mask):
    xdb, sbar = xbar[mask].mean(), S[mask].mean()
    half = 3 * sbar / (an(N_sub) * np.sqrt(N_sub))
    return xdb - half, xdb, xdb + half

# Round 1: all phase-1 subgroups.
phase1 = np.arange(phase1_end)
LCL, target, UCL = limits(phase1)
print(f"Round 1: LCL={LCL:.0f}, target={target:.0f}, UCL={UCL:.0f}")
# Round 1: LCL=1655, target=1677, UCL=1699

# Round 2: drop the phase-1 subgroups outside, then recompute.
inside = phase1[(xbar[phase1] >= LCL) & (xbar[phase1] <= UCL)]
LCL, target, UCL = limits(inside)
print(f"Round 2: LCL={LCL:.0f}, target={target:.0f}, UCL={UCL:.0f}")
# Round 2: LCL=1654, target=1676, UCL=1698

# Phase 2: subgroups 72 to 285 (boards ~501 to 2000).
x2 = xbar[phase1_end:phase2_end]
outside = int((x2 < LCL).sum() + (x2 > UCL).sum())
alpha = outside / len(x2)
print(f"Phase 2: {outside} of {len(x2)} outside, "
      f"alpha={100 * alpha:.1f}%, ARL={1 / alpha:.1f}")
# Phase 2: 6 of 214 outside, alpha=2.8%, ARL=35.7

# Part g: subgroup standard deviation rises over time, a sign the
# saw blades are slowly going out of alignment.
pd.Series(S[:phase2_end]).plot.line().update_layout(
    xaxis_title_text="Subgroup number",
    yaxis_title_text="Subgroup standard deviation").show()

Question

Your process with Cpk of 2.0 experiences a drift of \(1.5\sigma\) away from the current process operating point towards the closest specification limit. What is the new Cpk value; how many defects per million items did you have before the drift? And after the drift?

Solution

The new Cpk value is 1.5. The number of defects per million items at Cpk = 2.0 is 0.00099 (essentially no defects), while at Cpk = 1.5 it is 3.4 defects per million items. You only have to consider one-side of the distribution, since Cpk is by definition for an uncentered process, and deals with the side closest to the specification limits.

Python, 8 lines

from scipy.stats import norm

Cpk = 1.5
n_sigma_distance = 3 * Cpk
dpm = norm.cdf(-n_sigma_distance,
               loc=0,
               scale=1) * 1e6
print(f"Defects per million = {round(dpm, 3)}")

R, 6 lines

Cpk <- 1.5
n.sigma.distance <- 3 * Cpk
dpm <- pnorm(-n.sigma.distance,
             mean=0,
             sd=1) * 1E6
paste0('Defects per million = ', round(dpm,3))

Question

Which type of monitoring chart would be appropriate to detect unusual spikes (outliers) in your production process?

Solution

A Shewhart chart has no memory, and is suited to detecting unusual spikes in your production. CUSUM and EWMA charts have memory, and while they would pick up this spike, they would also create a long duration of false alarms after that. So those charts are much less appropriate.

Question

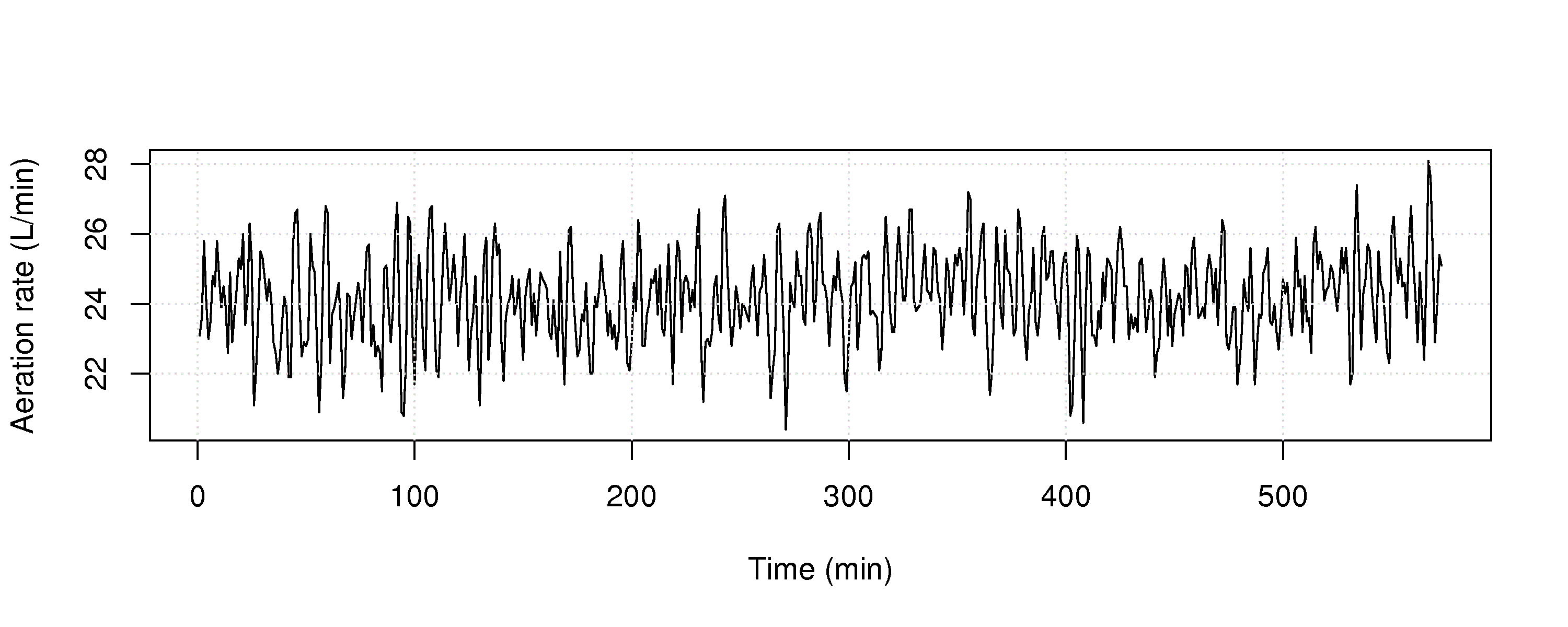
A tank uses small air bubbles to keep solid particles in suspension. If too much air is blown into the tank, then excessive foaming and loss of valuable solid product occurs; if too little air is blown into the tank the particles sink and drop out of suspension.

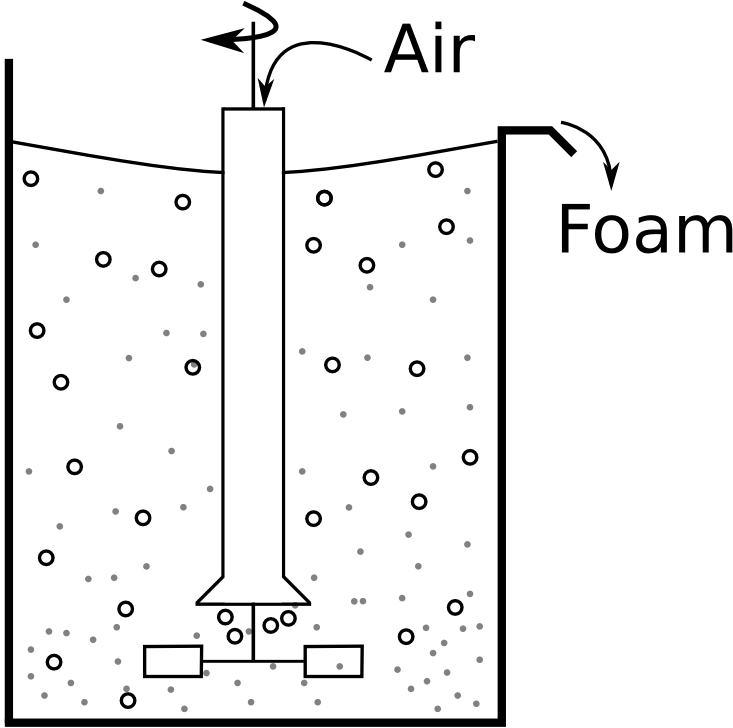
1. Which monitoring chart would you use to ensure the airflow is always near target?

2. Use the aeration rate dataset from the website and plot the raw data (total litres of air added in a 1 minute period). Are you able to detect any problems?

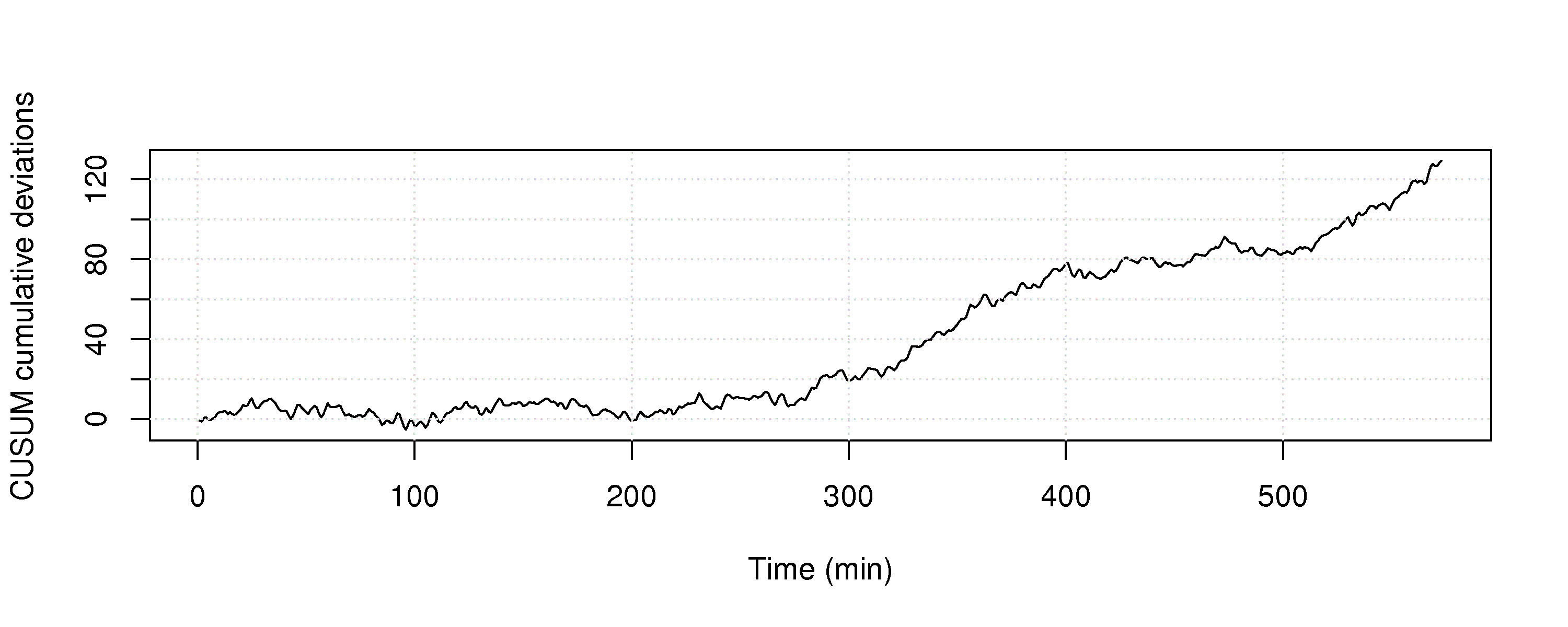
3. Construct the chart you described in part 1, and show it’s performance on all the data. Make any necessary assumptions to construct the chart.

4. At what point in time are you able to detect the problem, using this chart?

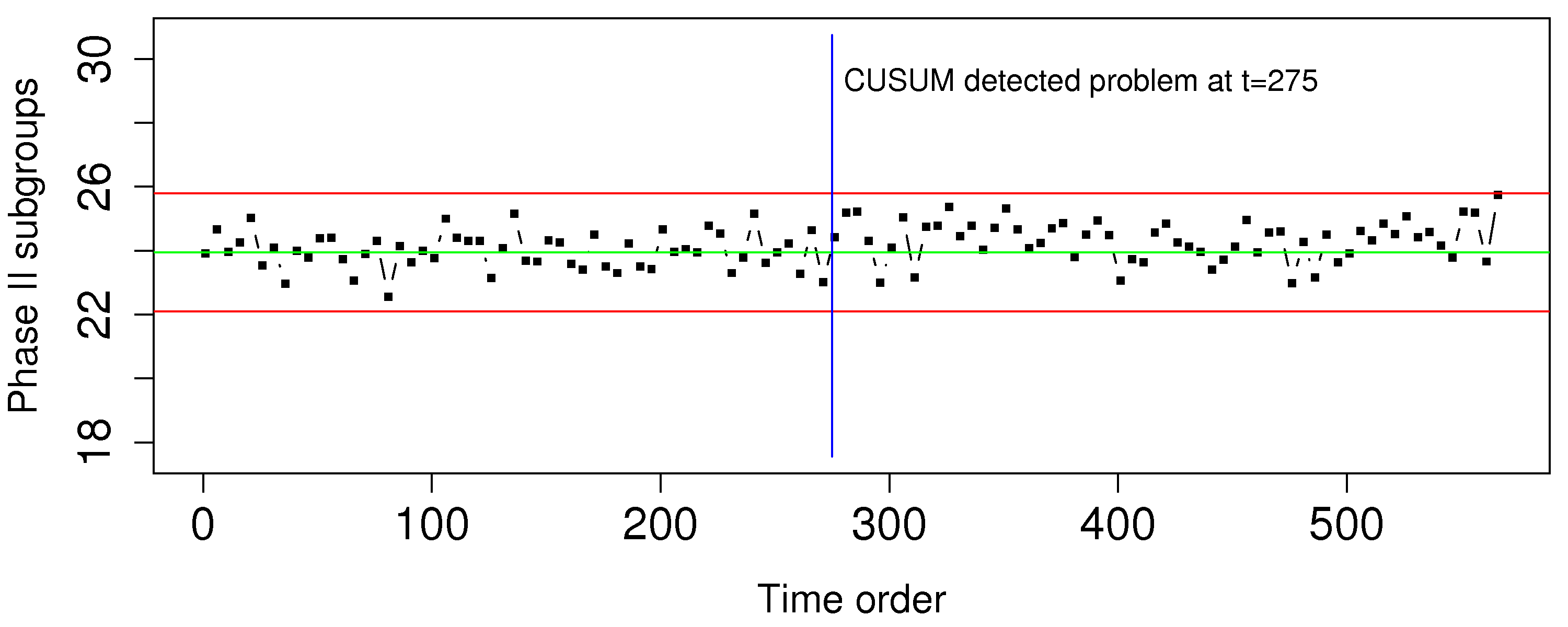
5. Construct a Shewhart chart, choosing appropriate data for phase 1, and calculate the Shewhart limits. Then use the entire dataset as if it were phase 2 data.

   • Show this phase 2 Shewhart chart.

   • Compare the Shewhart chart’s performance to the chart in part 3 of this question.

Solution

Solution based on work by Ryan and Stuart (2011 class)

1. A CUSUM chart would be a suitable chart to monitor that the airflow is near target. While a Shewhart chart is also intended to monitor the location of a variable, it has a much larger run length for detecting small shifts. An EWMA chart with small \(\lambda\) (long memory) would approximate a CUSUM chart, and so would also be suitable

2. The aeration rate dataset is depicted below:

   

   It is very difficult to assess problems from the raw data plot. There might be a slight upward shift around 300 and 500 minutes.

3. Assumptions for the CUSUM chart:

   • We will plot the CUSUM chart on raw data, though you could use subgroups if you wanted to.

   • The target value can be the mean (24.17) of all the data, or more robustly, use the median (24.1), especially if we expect problems with the raw data (true of almost every real data set).

4. The CUSUM chart, using the median as target value showed a problem starting to occur around \(t=300\). So we recalculated the median, using only data from 0 to \(t=200\), to avoid biasing the target value. Using this median instead, 23.95, we get the following CUSUM chart:

   

5. The revised CUSUM chart suggests that the error occurs around 275 min, as evidenced by the steep positive slope thereafter. It should be noted that the CUSUM chart begins to bear a positive slope around 200 min, but this initial increase in the cumulative error would likely not be diagnosable (i.e. using a V-mask).

   S, 59 lines

   # Code by Ryan and Stuart (2011 class)
   
   CUSUM <- function(x, target){
       N <- length(x)
       S <- numeric(N)
       S[1] = x[1] - target
       for (t in 2:N){        
           S[t] = S[t-1] + (x[t] - target)
       }
   return(S)
   }
   
   # Import data and remove missing values (NA)
   aeration.data <- read.csv('http://openmv.net/file/aeration-rate.csv')
   aeration <- na.omit(aeration.data$Aeration)
   
   # Plot raw data
   bitmap('aeration-rate-raw-data.png', type="png256", 
           width=10, height=4, res=300, pointsize=14)
   plot(aeration, type="l", xlab="Time (min)", ylab="Aeration rate (L/min)")
   grid()
   dev.off()
   
   # Plot CUSUM Chart
   target <- median(aeration[1:200])
   bitmap('aeration-CUSUM.png', type="png256", 
           width=10, height=4, res=300, pointsize=14)
   plot(CUSUM(aeration, target), type="l", xlab="Time (min)", 
        ylab="CUSUM cumulative deviations")
   grid()
   dev.off()
   
   # Plot the Shewhart chart: see code from the other question to 
   # calculate the control limits
   LCL <- 22.1
   UCL <- 25.8
   N <- 5
   subgroups <- matrix(aeration, N, length(aeration)/N)
   x.mean <- numeric(length(aeration)/N)
   x.sd <- numeric(length(aeration)/N)
   
   # Calculate mean and sd of subgroups (see R-tutorial)
   x.mean <- apply(subgroups, 2, mean)
   x.sd <- apply(subgroups, 2, sd)
   ylim <- range(x.mean) + c(-5, +5)
   xdb <- target  # use the same CUSUM target !
   
   bitmap('aeration-Shewhart-chart.png',
          type="png256", width=10, height=4, res=300, pointsize=14)
   par(mar=c(4.2, 4.2, 0.5, 0.5)) 
   par(cex.lab=1.3, cex.main=1.5, cex.sub=1.5, cex.axis=1.5)
   plot(seq(1,length(x.mean)*N, N), x.mean, type="b", pch=".", cex=5, main="", 
        ylab="Phase II subgroups", xlab="Time order", ylim=ylim)
   abline(h=UCL, col="red")
   abline(h=LCL, col="red")
   abline(h=xdb, col="green")
   lines(c(275, 275), ylim, col="blue")
   text(280, 29, "CUSUM detected problem at t=275",adj = c(0,0))
   dev.off()
   

6. Using the iterative Shewhart code from the previous question, we used

   • Phase I was taken far enough away from the suspected error: 0 - 200 min

   • Subgroup size of \(n=5\)

   • \(\bar{\bar{x}} = 23.9\)

   • \(\bar{S} = 1.28\)

   • \(a_n = 0.940\)

   • LCL = \(23.9 - 3\cdot\frac{1.28}{0.940\sqrt{5}}= 22.1\)

   • UCL = \(23.9 + 3\cdot\frac{1.28}{0.940\sqrt{5}}= 25.8\)

The Shewhart chart applied to the entire dataset is shown below. In contrast to the CUSUM chart, the Shewhart chart is unable to detect the problem in the aeration rate. Unlike the CUSUM chart, which has infinite memory, the Shewhart chart has no memory and cannot adequately assess the location of the monitored variable in relation to its specified target. Instead, the Shewhart chart merely monitors aeration rate with respect to the control limits for the process. Since the aeration rate does not exceed the control limits for the process (i.e. process remains in control), the Shewhart chart does not detect any abnormalities.

If you used the Western Electric rules, in addition to the Shewhart chart limits, you would have picked up a consecutive sequence of 8 points on one side of the target around \(t=350\).

The full solution in Python (the original R is in the literalinclude above):

Python, 36 lines

import numpy as np
import pandas as pd
from scipy.special import gamma

pd.options.plotting.backend = "plotly"

file = "https://openmv.net/file/aeration-rate.csv"
aeration = pd.read_csv(file)["Aeration"].to_numpy()

# Part 2: plot the raw data.
pd.Series(aeration).plot.line().update_layout(
    xaxis_title_text="Time [minutes]",
    yaxis_title_text="Aeration rate").show()

# Parts 3 and 4: CUSUM chart, using the median of the first
# 200 points (before the suspected problem) as a robust target.
target = np.median(aeration[:200])       # 23.95
S = np.cumsum(aeration - target)
print(f"mean={aeration.mean():.2f}, median={np.median(aeration):.2f}, "
      f"CUSUM target={target:.2f}")
pd.Series(S).plot.line(title="CUSUM chart").update_layout(
    xaxis_title_text="Time [minutes]",
    yaxis_title_text="Cumulative sum, S(t)").show()

# Part 5: Shewhart chart, phase 1 = first 200 points, subgroup n=5.
N_sub = 5
p1 = aeration[:200]
g = p1[: (len(p1) // N_sub) * N_sub].reshape(-1, N_sub).T
an = (np.sqrt(2) * gamma(N_sub / 2)
      / (np.sqrt(N_sub - 1) * gamma((N_sub - 1) / 2)))
xdb = g.mean(axis=0).mean()
sbar = g.std(axis=0, ddof=1).mean()
half = 3 * sbar / (an * np.sqrt(N_sub))
print(f"Shewhart phase 1: xbar={xdb:.1f}, Sbar={sbar:.2f}, "
      f"LCL={xdb - half:.1f}, UCL={xdb + half:.1f}")
# xbar=23.9, Sbar=1.28, LCL=22.1, UCL=25.8

Question

Do you think a Shewhart chart would be suitable for monitoring the closing price of a stock on the stock market? Please explain your answer if you agree, or describe an alternative if you disagree.

Solution

No, a Shewhart chart is not suitable for monitoring stock prices. Stock prices are volatile variables (not stable), so there is no sense in monitoring their location. Hopefully the stock is moving up, which it should on average, but the point is that stock prices are not stable. Nor are stock prices independent day-to-day.

So what aspect of a stock price is stable? The difference between the opening and closing price of a stock is remarkably stationary. Monitoring the day-to-day change in a stock price would work. Since you aren’t expected to know this fact, any reasonable answer that attempts to monitor a stable substitute for the price will be accepted. E.g. another alternative is to remove the linear up or down trend from a stock price and monitor the residuals.

There are many alternatives; if this sort of thing interests you, you might find the area called technical analysis worth investigating. An EWMA chart is widely used in this sort of analysis.

Question

Describe how a monitoring chart could be used to prevent over-control of a batch-to-batch process. (A batch-to-batch process is one where a batch of materials is processed, followed by another batch, and so on).

Solution

Over-control of any process takes place when too much corrective action is applied. Using the language of feedback control, your gain is the right sign, but the magnitude is too large. Batch processes are often subject to this phenomenon: e.g. the operator reduces the set-point temperature for the next batch, because the current batch produced product with a viscosity that was too high. But then the next batch has a viscosity that is too low, so the operator increases the temperature set-point for the following batch. This constant switching is known as over-control (the operator is the feedback controller and his/her gain is too high, i.e. they are over-reacting).

A monitoring chart such as a Shewhart chart would help the operator: if the previous batch was within the limits, then s/he should not take any corrective action. Only take action when the viscosity value is outside the limits. An EWMA chart would additionally provide a one-step ahead prediction, which is an advantage.

Question

You need to construct a Shewhart chart. You go to your company’s database and extract data from 10 periods of time lasting 6 hours each. Each time period is taken approximately 1 month apart so that you get a representative data set that covers roughly 1 year of process operation. You choose these time periods so that you are confident each one was from in control operation. Putting these 10 periods of data together, you get one long vector that now represents your phase 1 data.

• There are 8900 samples of data in this phase 1 data vector.

• You form subgroups: there are 4 samples per subgroup and 2225 subgroups.

• You calculate the mean within each subgroup (i.e. 2225 means). The mean of those 2225 means is 714.

• The standard deviation within each subgroup is calculated; the mean of those 2225 standard deviations is 98.

1. Give an unbiased estimate of the process standard deviation?

2. Calculate lower and upper control limits for operation at \(\pm 3\) of these standard deviations from target. These are called the action limits.

3. Operators like warning limits on their charts, so they don’t have to wait until an action limit alarm occurs. Discussions with the operators indicate that lines at 590 and 820 might be good warning limits. What percentage of in control operation will lie inside the proposed warning limit region?

Solution

1. An unbiased estimate of the process standard deviation is \(\hat{\sigma} = \frac{\overline{S}}{a_n} = \frac{98}{0.921} = \mathrm{106.4}\), since the subgroup size is \(n=4\).

2. Using the data provided in the question:

   \[\begin{split}\text{UCL} &= \overline{\overline{x}} + 3 \frac{\overline{S}}{a_n \sqrt{n}} = 714 + 3 \times \frac{98}{0.921 \times 2 } = \mathrm{874} \\ \text{LCL} &= \overline{\overline{x}} - 3 \frac{\overline{S}}{a_n \sqrt{n}} = 714 - 3 \times \frac{98}{0.921 \times 2 } = \mathrm{554}\end{split}\]

3. Since Shewhart charts assume a normal distribution in their derivation, we can use the same principle to calculate a \(z\)-value, and the fraction of the area under the distribution. But you have to be careful here: which standard deviation do you use to calculate the \(z\)-value? You should use the subgroup’s standard deviation, not the process standard deviation. The Shewhart chart shows the subgroup averages, so the values of 590 and 820 refer to the subgroup values.

If that explanation doesn’t make sense, think of the central limit theorem: the mean of a group of samples, \(\overline{x} \sim \mathcal{N}\left(\mu, \sigma^2/n\right)\), where \(\sigma^2\) is the process variance, and \(\sigma^2/n\) is the subgroup variance of \(\overline{x}\).

\[\begin{split}z_{\text{low}} &= \frac{x_\text{low} - \overline{\overline{x}}}{\hat{\sigma}/\sqrt{n}} = \frac{590 - 714}{106.4/\sqrt{4}} = -2.33 \\ z_{\text{high}} &= \frac{x_\text{high} - \overline{\overline{x}}}{\hat{\sigma}/\sqrt{n}} =\frac{820 - 714}{106.4/\sqrt{4}} = +2.00\end{split}\]

The area below -2.33 is pnorm(-2.33) = 0.009903076, though I will accept any value around 1%, eyeballed from the printed tables. The area below +2.00 is 97.73%, which was on the tables already. So the total amount of normal operation within the warning limits is 97.73-1.00 = 96.7%.

The asymmetry in their chosen warning limits might be because a violation of the lower bound is more serious than the upper bound.

Question

If an exponentially weighted moving average (EWMA) chart can be made to approximate either a CUSUM or a Shewhart chart by adjusting the value of \(\lambda\), what is an advantage of the EWMA chart over the other two? Describe a specific situation where you can benefit from this.

Solution

The EWMA chart not only provides control limits for monitoring a process, it also provides a one-step-ahead prediction of the variable being monitored. This is particularly beneficial as the EWMA chart’s prediction can be used to adjust process conditions, should the prediction show the process heading towards, or outside, the control limits. This means that changes to the process are only made if they are required. This is extremely important on slow-moving processes, which are prone to overly aggressive control.

Question

The most recent estimate of the process capability ratio for a key quality variable was 1.30, and the average quality value was 64.0. Your process operates closer to the lower specification limit of 56.0. The upper specification limit is 93.0.

What are the two parameters of the system you could adjust, and by how much, to achieve a capability ratio of 1.67, required by recent safety regulations. Assume you can adjust these parameters independently.

Solution

The process capability ratio for an uncentered process, \(\text{PCR}_\text{k}\), is given by:

\[\text{PCR}_\text{k} = \min \left( \frac{\text{Upper specification limit} - \overline{\overline{x}}}{3\sigma}; \frac{\overline{\overline{x}} - \text{Lower specification limit}}{3\sigma} \right)\]

The two adjustable parameters are \(\overline{\overline{x}}\), the process target (operating point) and \(\sigma\), the process standard deviation. The current process standard deviation is:

\[\begin{split}1.30 &= \frac{64.0 - 56.0}{3\sigma} \\ \sigma &= \frac{64.0 - 56.0}{3 \times 1.30} = 2.05\end{split}\]

• Adjusting the operating point (we would expect to move the operating point away from the LSL):

  \[\begin{split}1.67 &= \frac{\overline{\overline{x}} - 56.0}{3 \times 2.05}\\ \overline{\overline{x}} &= 56.0 + 1.67 \times 3 \times 2.05 = 66.3\end{split}\]

  So the operating point increases from 64.0 to 66.3 to obtain a higher capability ratio.

• Adjusting the process standard deviation (we would have to assume we can decrease the standard deviation, keeping the operating point fixed):

  \[\begin{split}1.67 &= \frac{64.0 - 56.0}{3 \times \sigma}\\ \sigma &= \frac{64.0 - 56.0}{3 \times 1.67} = 1.60\end{split}\]

  Decrease the process standard deviation from 2.05 to 1.60.

Question

A bagging system fills bags with a target weight of 37.4 grams and the lower specification limit is 35.0 grams. Assume the bagging system fills the bags with a standard deviation of 0.8 grams:

1. What is the current Cpk of the process?

2. To what target weight would you have to set the bagging system to obtain Cpk=1.3?

3. How can you adjust the Cpk to 1.3 without adjusting the target weight (i.e. keep the target weight at 37.4 grams)?

Solution

1. Recall the Cpk is defined relative to the closest specification limit. So in this case it must be due to the lower limit. Cpk = \(\frac{\overline{\overline{x}} - LSL}{3\sigma} = \frac{37.4 - 35.0}{3 \times 0.8} = \mathrm{1.0}\)

2. To obtain Cpk = 1.3 we solve the above equation for \(\overline{\overline{x}} = 1.3 \times 3 \times 0.8 + 35.0 = \mathrm{38.12}\) grams.

3. Changing the lower specification limit is not an option to raise Cpk, because the bags are sold as containing 35.0 grams of snackfood. Changing the specification limit is in general an artificial way of changing Cpk. The only practical way to improve Cpk is to decrease the process variance (e.g. using better equipment with tighter control). The new \(\sigma = \frac{37.4 - 35.0}{3 \times 1.3} = \mathrm{0.615}\) grams.

Question

Plastic sheets are manufactured on your blown film line. The Cp value is 1.7. You sell the plastic sheets to your customers with specification of 2 mm \(\pm\) 0.4 mm.

1. List three important assumptions you must make to interpret the Cp value.

2. What is the theoretical process standard deviation, \(\sigma\)?

3. What would be the Shewhart chart limits for this system using subgroups of size \(n=4\)?

4. Illustrate your answer from part 2 and 3 of this question on a diagram of the normal distribution.

Solution

1. The notes show that Cp values require us to assume that (a) the process values follow a normal distribution, the process was centered when the data were collected, and (c) that the process was stable (use a monitoring chart to verify this last assumption).

2. The range from the lower to the upper specification limit is 0.8 mm, which spans 6 standard deviations. Given the Cp value of 1.7, the process standard deviation must have been \(\sigma = \frac{0.8}{1.7 \times 6} = \mathrm{0.0784}\) mm.

3. This time we have the process standard deviation, so there is no need to estimate it from historical phase 1 data (remember the assumption that Cp and Cpk value are calculated from stable process operation?). The Shewhart control limits would be: \(\overline{\overline{x}} \pm 3 \times \frac{\sigma}{\sqrt{n}} = 2 \pm 3 \times 0.0784 / 2\). The LCL = 1.88 mm and the UCL = 2.12 mm.

4. An illustration is shown here with the USL, LSL, LCL and UCL, and target values. This question merely required you to show the LCL and UCL within the LSL and USL, on any normal distribution curve. However, for illustration, I have added to the diagram the distribution for the Shewhart chart (thicker line) and distribution for the raw process data (thinner line).

The numbers in parts 2 and 3, in Python:

Python, 13 lines

import numpy as np

# Cp relates the specification width to 6 standard deviations.
Cp = 1.7
USL, LSL = 2.0 + 0.4, 2.0 - 0.4
sigma = (USL - LSL) / (Cp * 6)
print(f"Process standard deviation = {sigma:.4f} mm")   # 0.0784

# Shewhart limits for subgroups of size n = 4, at the target.
n, target = 4, 2.0
LCL = target - 3 * sigma / np.sqrt(n)
UCL = target + 3 * sigma / np.sqrt(n)
print(f"LCL = {LCL:.2f} mm, UCL = {UCL:.2f} mm")   # 1.88, 2.12

The R code used to generate the figure:

S, 41 lines

n = 4                   # subgroup size
Cp = 1.7
x.range = 0.8
x.sd = x.range/Cp/6     # process std.dev.
x.bar = 2               # process target
LSL = x.bar - 0.4
USL = x.bar + 0.4
LCL = x.bar - 3 * x.sd / sqrt(n)
UCL = x.bar + 3 * x.sd / sqrt(n)

# A vector of 500 equally spaced points, with 10% offset on either side
x <- seq(LSL-0.1*x.range, USL+0.1*x.range, x.range/500)  
px <- dnorm(x, mean=x.bar, sd=x.sd)
p.shewhart <- dnorm(x, mean=x.bar, sd=x.sd/sqrt(n))

plot(x, p.shewhart, type="l", xlab=(expression(""*x)), ylab="", frame.plot=FALSE, 
                    main=(expression(""*mu*"=2.0")), xlim=c(LSL, USL), cex.lab=1.8, 
                    cex.main=1.8, lwd=3, cex.sub=1.8, cex.axis=1.8, yaxt="n")
lines(x, px, type="l", col="gray50")
abline(v=x.bar)

upper.limit = max(p.shewhart)*0.8
segments(x0=LSL,y0=0, x1=LSL, y1=upper.limit, col="gray30")
segments(x0=USL,y0=0, x1=USL, y1=upper.limit, col="gray30")
segments(x0=LCL,y0=0, x1=LCL, y1=upper.limit, col="red")
segments(x0=UCL,y0=0, x1=UCL, y1=upper.limit, col="red")
text(LSL, upper.limit, "LSL", cex=1.3, pos=3)
text(USL, upper.limit, "USL", cex=1.3, pos=3)
text(LCL, upper.limit, "LCL", cex=1.3, pos=3)
text(UCL, upper.limit, "UCL", cex=1.3, pos=3)

# Sigma for the process
y <- dnorm(x.bar+x.sd, mean=x.bar, sd=x.sd)
arrows(x0=x.bar, y0=y, x1=x.bar+x.sd, y1=y, code=3, angle=15, length=0.1) 
text(x.bar + x.sd, y+0.2, (expression(""*sigma)), cex=1.8, pos=4)

# Sigma for the Shewhart chart
y <- dnorm(x.bar+x.sd/sqrt(n), mean=x.bar, sd=x.sd/sqrt(n))
arrows(x0=x.bar, y0=y, x1=x.bar+x.sd/sqrt(n), y1=y, code=3, angle=15, length=0.1) 
text(x.bar+x.sd/sqrt(n), y+0.2, (expression(""*sigma/sqrt(n))), cex=1.8, pos=4)

Question

The following charts show the weight of feed entering your reactor. The variation in product quality leaving the reactor was unacceptably high during this period of time.

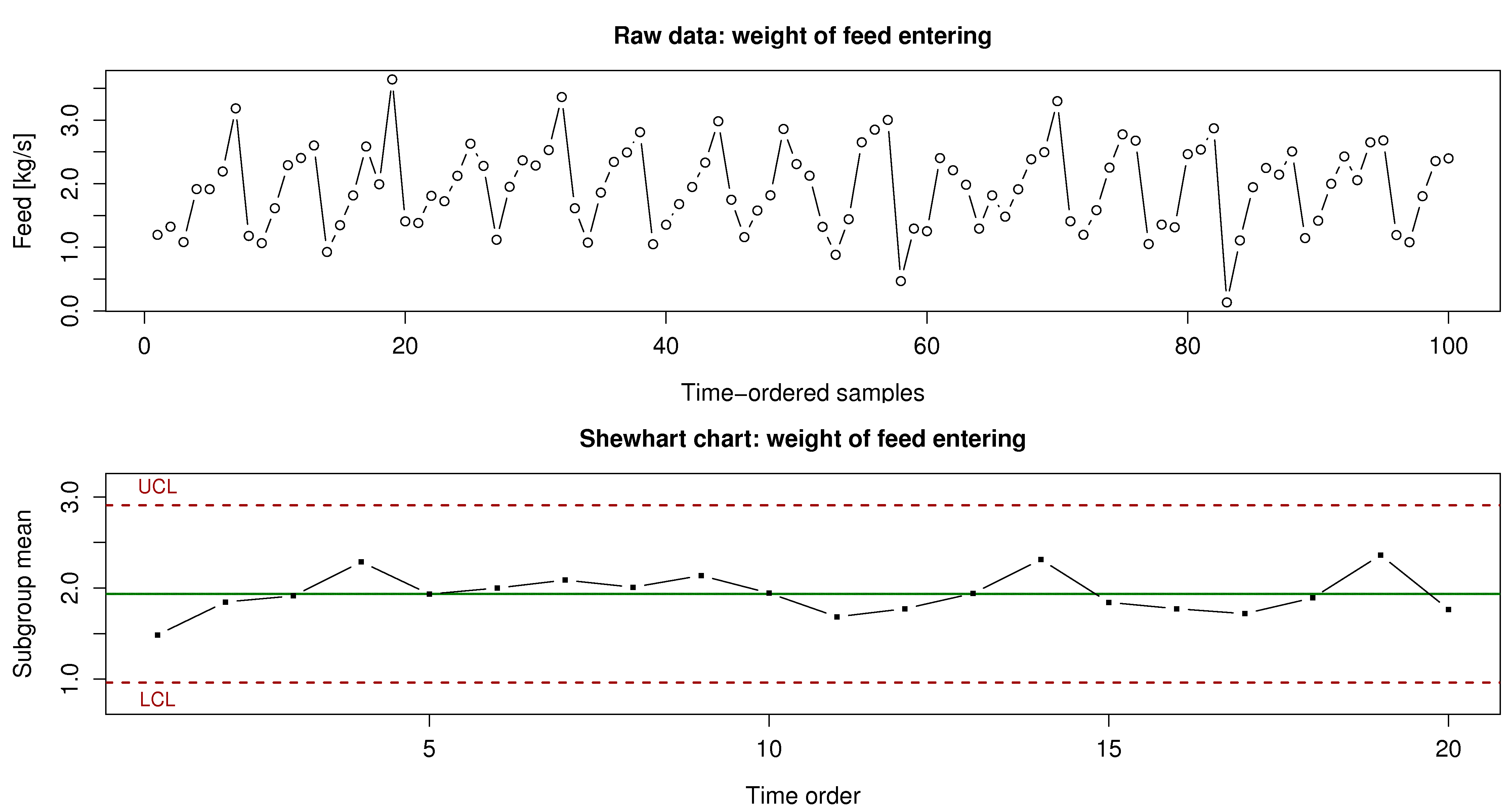
1. What can your group of process engineers learn about the problem, using the time-series plot (100 consecutive measurements, taken 1 minute apart).

2. Why is this variability not seen in the Shewhart chart?

3. Using concepts described elsewhere in this book, why might this sort of input to the reactor have an effect on the quality of the product leaving the reactor?

Solution

1. The time-series plot shows a cyclical, almost saw-tooth, pattern in the weight of feed entering. I would investigate the feeding equipment to see what is leading to these fluctuations in the feed weight. Perhaps some rotary device is responsible for the periodic variation.

2. The variability is not seen in the Shewhart monitoring chart. The Shewhart chart used subgroups of size 5 (20 Shewhart samples for 100 time-series samples). These fluctuations obviously cancel out when calculating the Shewhart subgroups (a limitation of the Shewhart chart).

3. As engineers we are aiming for stability in our processes; stability in the raw material characteristics, stability in how we operate the process over time and minimizing as many disturbances as possible. If we can do this, it will lead to greatly improved consistency in our products (low output variability). Having this sort of input to the reactor means we have to provide apply (feedback) control to counteract it. In this case the feedback control may not have been effective to eliminate the feed variation, or the feedback control itself caused other disruptions to the process quality.

Question

You will come across these terms in the workplace. Investigate one of these topics, using the Wikipedia link below to kick-start your research. Write a paragraph that (a) describes what your topic is and (b) how it can be used when you start working in a company after you graduate, or how you can use it now if you are currently working.

• Lean manufacturing

• Six sigma and the DMAIC cycle. See the list of companies that use six sigma tools.

• Kaizen (a component of The Toyota Way)

• Genchi Genbutsu (also a component of The Toyota Way)

In early 2010 Toyota experienced some of its worst press coverage on this very topic. Here is an article in case you missed it.

Question

The Kappa number is a widely used measurement in the pulp and paper industry. It can be measured on-line, and indicates the severity of chemical treatment that must be applied to a wood pulp to obtain a given level of whiteness (i.e. the pulp’s bleachability). Data on the website contain the Kappa values from a pulp mill. Use the first 2000 data points to construct a Shewhart monitoring chart for the Kappa number. You may use any subgroup size you like. Then use the remaining data as your phase 2 (testing) data. Does the chart perform as expected?

Solution

The intention of this question is for you to experience the process of iteratively calculating limits from phase 1 data and applying them to phase 2 data.

The raw data for the entire data set looks as follows. There are already regions in the phase 2 data that we expect to not be from normal operation (around 2500 and 2900)

I used subgroups of size 6 for the figures in this answer, however, the code below is very general, and you can regenerate the plots if you chose a different subgroup size. Just change one of the lines near the top.

The upper and lower control limits are calculated, and with a subgroup size of \(n=6\), there are 333 subgroups and the limits are: LCL = 18.26, target = 21.73, and UCL = 25.21. This is illustrated on the phase 1 data here:

Next we remove the subgroups which lie outside the limits. Please try using the code to see how to do it automatically. The new limits, after removing the subgroups beyond the limits from the first round are: LCL = 18.24, target = 21.71 and UCL = 25.19. They barely changed. But the updated plot with subgroups removed is now shown below. There is no need to perform another round of pruning. Only if you used a subgroup size of 4 would you need to do a third round. You could also have just shifted the limits to a different level, for example, to \(\pm 4\) standard deviations. We can do this if we have enough process knowledge to understand the implication of it, in terms of profit.

Now apply these control limits to the phase 2 data. The plot is shown below:

The limits identify 2 prolonged periods of unusual operation at sequence point 80 and 140. If we apply the Western Electric rules, we see a third unusual region around sequence step 220. A few other alarms are scattered in the phase 2 data. About 7% of the subgroups lie outside these control limits, so these phase 2 data are definitely not from in-control operation; which we expected from the raw data plot at the start of this question.

The code for all the calculation steps is provided here in Python, followed by the original R:

Python, 44 lines

import numpy as np
import pandas as pd
from scipy.special import gamma

pd.options.plotting.backend = "plotly"

file = "https://openmv.net/file/kappa-number.csv"
kappa = pd.read_csv(file)["Kappa"].to_numpy()

N_sub = 6              # subgroup size; try other sizes too
phase1 = kappa[:2000]  # the first 2000 points are phase 1

def an(n):
    return (np.sqrt(2) * gamma(n / 2)
            / (np.sqrt(n - 1) * gamma((n - 1) / 2)))

def shewhart_limits(x):
    """Subgroup ``x`` into columns of N_sub and return the subgroup
    means together with the (LCL, target, UCL) Shewhart limits."""
    g = x[: (len(x) // N_sub) * N_sub].reshape(-1, N_sub).T
    xbar, S = g.mean(axis=0), g.std(axis=0, ddof=1)
    xdb, sbar = xbar.mean(), S.mean()
    half = 3 * sbar / (an(N_sub) * np.sqrt(N_sub))
    return xbar, xdb - half, xdb, xdb + half

# Round 1: all phase-1 subgroups.
xbar, LCL, target, UCL = shewhart_limits(phase1)
print(f"Round 1: LCL={LCL:.2f}, target={target:.2f}, UCL={UCL:.2f}")
# Round 1: LCL=18.26, target=21.73, UCL=25.21

# Round 2: drop the subgroups that fell outside, then recompute.
keep = (xbar >= LCL) & (xbar <= UCL)
kept = phase1[: len(xbar) * N_sub].reshape(-1, N_sub)[keep].ravel()
_, LCL, target, UCL = shewhart_limits(kept)
print(f"Round 2: LCL={LCL:.2f}, target={target:.2f}, UCL={UCL:.2f}")
# Round 2: LCL=18.24, target=21.71, UCL=25.19

# Phase 2: everything after the first 2000 points.
phase2 = kappa[2000:]
g2 = phase2[: (len(phase2) // N_sub) * N_sub].reshape(-1, N_sub).T
x2 = g2.mean(axis=0)
frac = ((x2 < LCL) | (x2 > UCL)).mean()
print(f"Phase 2 fraction outside limits = {100 * frac:.1f}%")
# Phase 2 fraction outside limits = 7.1%

S, 131 lines

kappa <- read.csv('http://openmv.net/file/kappa-number.csv')
summary(kappa)
attach(kappa)    # gives access to the variable "Kappa"

N.all <- length(Kappa)
N.phase1 <- 2000
N.phase2 <- N.all - N.phase1
N.subgroup <- 5

phase1.start <- 1
phase1.end <- floor(N.phase1/N.subgroup)
phase2.start <- phase1.end + 1
phase2.end <- floor(N.all/N.subgroup)

# Plot all the data
plot(Kappa, type="p", pch=".", cex=2, main="", ylab="Kappa number: raw data", 
     xlab="Sequence order")
abline(v=N.phase1, col="gray50")
text(N.phase1/2, 10, "Phase I data", col="blue")
text(N.phase1 + N.phase2/2, 10, "Phase II data", col="blue")

# We won't check the phase I raw data for outliers; we will use the phase I 
# subgroups to check for outliers.

# Create the subgroups on ALL the raw data.  Form a matrix with `N.subgroup` rows
# placing the vector of data down each row, then going across to form the columns.

# Calculate the mean and standard deviation within each subgroup (columns of the matrix)
reshaped.data <- matrix(Kappa, N.subgroup, N.all/N.subgroup)
subgroup.x.bar <- apply(reshaped.data, 2, mean)
subgroup.S <- apply(reshaped.data, 2, sd)

phase1.xbar <- subgroup.x.bar[phase1.start:phase1.end]
phase1.S <- subgroup.S[phase1.start:phase1.end]
phase2.xbar <- subgroup.x.bar[phase2.start:phase2.end]
phase2.S <- subgroup.S[phase2.start:phase2.end]

# We are going to repeatedly have to calculate the phase 1 limits.  Create a function.
shewhart_limits <- function(xbar, S, subgroup.size, N.stdev=3){
    # Give the xbar and S vector containing the subgroup means and standard deviations.
    # Also give the subgroup size used.  Returns the lower and upper control limits
    # for the Shewhart chart (UCL and LCL) which are N.stdev away from the target.
    
    x.double.bar <- mean(xbar)     
    s.bar <- mean(S)
    an = c(NA, 0.793, 0.886, 0.921, 0.940, 0.952, 0.959, 0.965)
    LCL <- x.double.bar - 3*s.bar/an[subgroup.size]/sqrt(subgroup.size)
    UCL <- x.double.bar + 3*s.bar/an[subgroup.size]/sqrt(subgroup.size)
    c(LCL, UCL)
    
return(list(LCL, x.double.bar, UCL))
}
limits <- shewhart_limits(phase1.xbar, phase1.S, N.subgroup)
LCL <- limits[1]
xdb <- limits[2]
UCL <- limits[3]
c(LCL, xdb, UCL)

# Any points outside these limits?  Yup, quite a few.
plot(phase1.xbar, type="b", pch=".", cex=5, main="", ylab="Phase I subgroups: round 1", 
     xlab="Sequence order")
abline(h=UCL, col="red")
abline(h=LCL, col="red")
abline(h=xdb, col="green")
lines(phase1.xbar, type="b", pch=".", cex=5)

# Find the indices of the point outside the limits.  You could use the identify function,
# or you can find them programatically, using boolean (logical) vectors.  Take a look 
# at what the variables "outside" and "inside" look like to understand what they do.
outside <- (phase1.xbar > UCL) + (phase1.xbar < LCL)
outside <- as.logical(outside)
inside <- !outside     

# Now use only the data inside the existing limits to recalculate the phase I limits.
phase1.xbar <- phase1.xbar[inside]
phase1.S <- phase1.S[inside]
limits <- shewhart_limits(phase1.xbar, phase1.S, N.subgroup)
LCL <- limits[1]
xdb <- limits[2]
UCL <- limits[3]
c(LCL, xdb, UCL)

# Replot the data: everything is inside the limits this time
plot(phase1.xbar, type="b", pch=".", cex=5, main="", ylab="Phase I subgroups: round 2", 
     xlab="Sequence order")
abline(h=UCL, col="red")
abline(h=LCL, col="red")
abline(h=xdb, col="green")
lines(phase1.xbar, type="b", pch=".", cex=5)

outside <- (phase1.xbar > UCL) + (phase1.xbar < LCL)
sum(outside)  # yay, it is zero!

# Using subgroups of size 4 or smaller will require an additional
# round of pruning subgroups  
outside <- as.logical(outside)
inside <- !outside
phase1.xbar <- phase1.xbar[inside]
phase1.S <- phase1.S[inside]
limits <- shewhart_limits(phase1.xbar, phase1.S, N.subgroup)
LCL <- limits[1]
xdb <- limits[2]
UCL <- limits[3]
c(LCL, xdb, UCL)

# Replot the data: everything is inside the limits after the second
# or third round of pruning.
plot(phase1.xbar, type="b", pch=".", cex=5, main="", ylab="Phase I subgroups: round 3", 
    xlab="Sequence order")
abline(h=UCL, col="red")
abline(h=LCL, col="red")
abline(h=xdb, col="green")
lines(phase1.xbar, type="b", pch=".", cex=5)

outside <- (phase1.xbar > UCL) + (phase1.xbar < LCL)
sum(outside)  # yeah, it is zero!

# Now test the Shewhart limits on the phase II data
plot(phase2.xbar, type="b", pch=".", cex=5, main="", ylab="Phase II subgroups: testing", 
     xlab="Sequence order")
abline(h=UCL, col="red")
abline(h=LCL, col="red")
abline(h=xdb, col="green")
lines(phase2.xbar, type="b", pch=".", cex=5)
outside.phase2 <- (phase2.xbar > UCL) + (phase2.xbar < LCL)
alpha <- sum(outside.phase2) / length(phase2.xbar)
alpha  

# Alpha = 7.9% for this phase 2 data, much higher than the 0.27% expected for 
# 3 sigma limits to be expected, because there are process problems on at 
# least 3 occasions in this phase 2 data.

Question

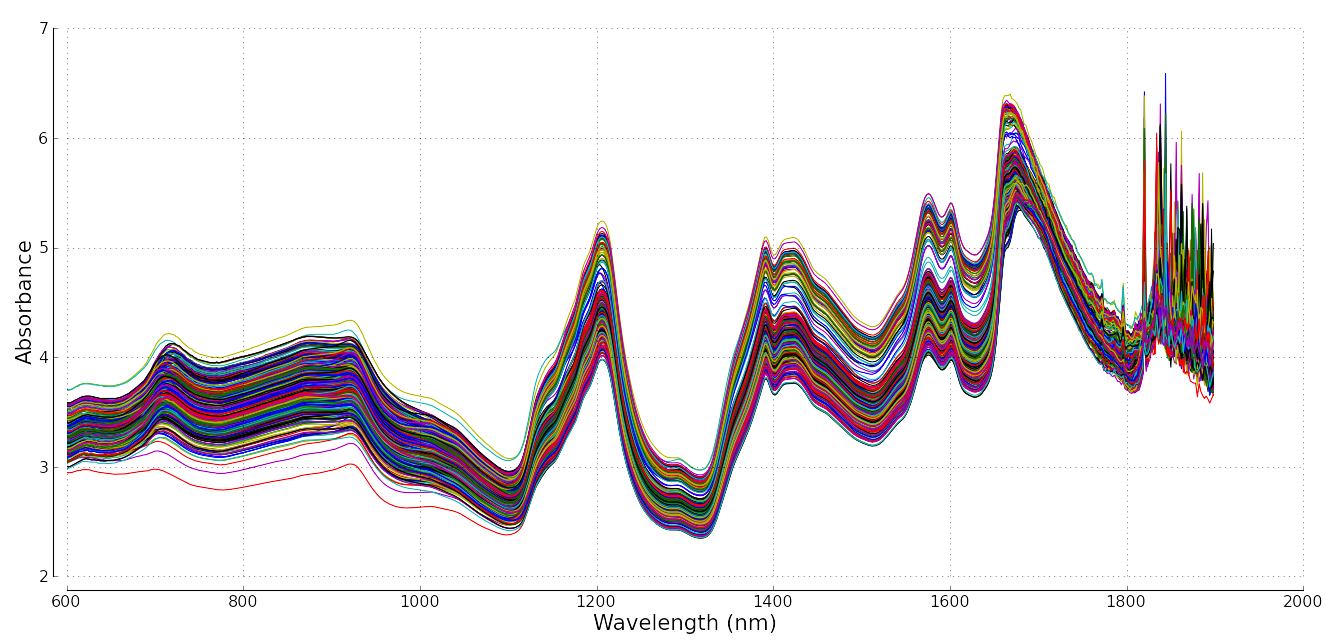
In this section we showed how one can monitor any variable in a process. Modern instrumentation though capture a wider variety of data. It is common to measure point values, e.g. temperature, pressure, concentration and other hard-to-measure values. But it is increasingly common to measure spectral data. These spectral data are a vector of numbers instead of a single number.

Below is an example from a pharmaceutical process: a complete spectrum can be acquired many times per minute, and it gives a complete chemical fingerprint or signature of the system. There are 460 spectra in figure below; they could have come, for example, from a process where they are measured 5 seconds apart. It is common to find fibre optic probes embedded into pipelines and reactors to monitor the progress of a reaction or mixing.

Write a few bullet points how you might monitor a process where a spectrum (a vector) is your data source, and not a “traditional” single point measurement, like a temperature value.

Solution

A complete spectrum (vector) of values is obtained with every observation. To monitor a process using one of the charts learned about so far (Shewhart, CUSUM, or EWMA chart) we have to reduce this vector down to a single number. Any of these methods will do:

• Use a single point at a particular wavelength in the spectrum (e.g. the peak at 1200 nm or 1675 nm).

• Use a weighted sum of a region of the spectrum, or the integrated area under a region in the spectrum (these 2 approaches are similar/equivalent)

• Use the spectrum to predict a certain property of interest, and then monitor that property instead. For example: use the spectrum to predict the colour of cookies (i.e. how well baked they are) and monitor the “well-bakedness” characteristic.

Later on we will learn about multivariate monitoring methods.

Question

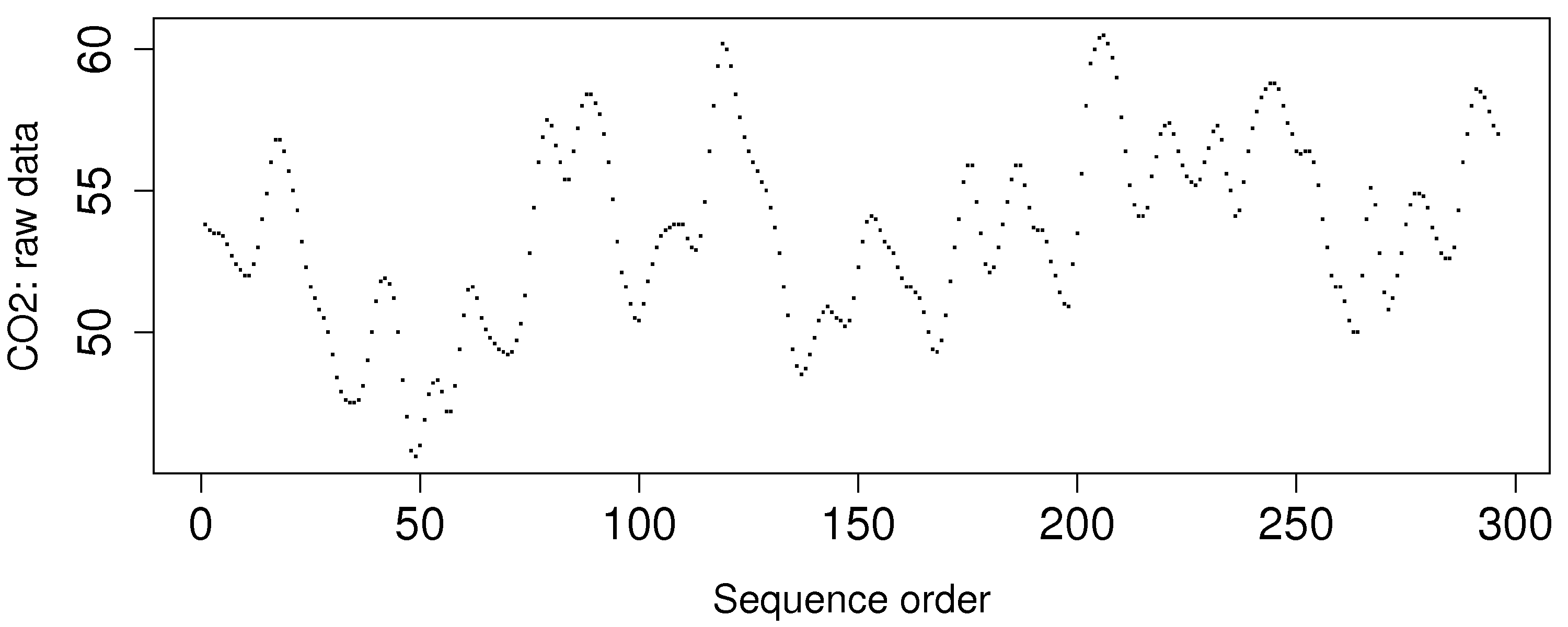
The carbon dioxide measurement is available from a gas-fired furnace. These data are from phase 1 operation.

1. Calculate the Shewhart chart upper and lower control limits that you would use during phase 2 with a subgroup size of \(n=6\).

2. Is this a useful monitoring chart? What is going in this data?

3. How can you fix the problem?

Solution

Solution based on work by Ryan and Stuart (2011 class)

First a plot of the raw data will be useful:

1. Assuming that the CO₂ data set is from phase 1 operation, the control limits were calculated as follows:

   • Assume subgroups are independent

   • \(\bar{\bar{x}} =\frac{1}{K}\sum\limits_{k=1}^K\bar{x}_k= 53.5\)

   • \(\bar{S} =\frac{1}{K}\sum\limits_{k=1}^K s_k= 1.10\)

   • \(a_n =0.952\)

   • LCL = \(53.5 -3 \cdot\frac{1.10}{0.952\sqrt{6}} = 52.08\)

   • UCL = \(53.5 +3 \cdot\frac{1.10}{0.952\sqrt{6}} = 54.92\)

2. The Shewhart chart using a subgroup of size 6 is not a useful monitoring chart. There are too many false alarms, which will cause the operators to just ignore the chart. The problem is that the first assumption of independence is not correct and has a detrimental effect, as shown in a previous question.

   

3. One approach to fixing the problem is to subsample the data, i.e. only use every \(k^\text{th}\) data point as the raw data, e.g. \(k=10\), and then form subgroups from that sampled data.

   Another is to use a larger subgroup size. Use the autocorrelation function, and the corresponding acf(...) function in R to verify the degree of relationship. Using this function we can see the raw data are unrelated after the 17th lag, so we could use subgroups of that size. However, even then we see the Shewhart chart showing frequent violation, though fewer than before.

   Yet another alternative is to use an EWMA chart, which takes the autocorrelation into account. However, the EWMA chart limits are found from the assumption that the subgroup means (or raw data, if subgroup size is 1), are independent.

   So we are finally left with the conclusion that perhaps there data really are not from in control operation, or, if they are, we must manually adjust the limits to be wider.

Python, 73 lines

import numpy as np
import pandas as pd
from scipy.special import gamma
from statsmodels.graphics.tsaplots import plot_acf

pd.options.plotting.backend = "plotly"

file = "https://openmv.net/file/gas-furnace.csv"
data = pd.read_csv(file)
CO2 = data["CO2"].to_numpy()
N_raw = len(CO2)
N_sub = 6

# Change N_sub to 10, 15, 20, etc.
# At N_sub = 17 we see the
# autocorrelation disappear.

# Plot all the data.
raw = pd.DataFrame({"Sequence order": np.arange(N_raw), "CO2": CO2})
raw.plot.scatter(x="Sequence order", y="CO2").update_layout(
    yaxis_title_text="CO2: raw data").show()

# Create the subgroups on ALL the raw data.
# Drop the last few samples so the count is a
# multiple of N_sub, then reshape into N_sub rows
# by N_raw/N_sub columns; each column is one
# subgroup. Calculate the mean and standard
# deviation within each subgroup.
N_groups = N_raw // N_sub
subgroups = CO2[: N_groups * N_sub].reshape(N_groups, N_sub).T
subgroups_S = subgroups.std(axis=0, ddof=1)
subgroups_xbar = subgroups.mean(axis=0)
ylim = (subgroups_xbar.min() - 3,
        subgroups_xbar.max() + 3)

# Keep adjusting N_sub until you don't see
# any autocorrelation between subgroups.
plot_acf(subgroups_xbar)

# Create a function to calculate Shewhart
# chart limits.
def shewhart_limits(xbar, S, sub_n,
                    N_stdev=3):
    """Return (LCL, xdb, UCL) which are
    N_stdev away from the target, given the
    subgroup means xbar, subgroup standard
    deviations S, and subgroup size sub_n."""
    xdb = xbar.mean()  # x-double-bar
    s_bar = S.mean()
    num_an = np.sqrt(2) * gamma(sub_n / 2)
    den_an = np.sqrt(sub_n - 1) * gamma(
        (sub_n - 1) / 2)
    an = num_an / den_an
    LCL = xdb - N_stdev * s_bar / (
        an * np.sqrt(sub_n))
    UCL = xdb + N_stdev * s_bar / (
        an * np.sqrt(sub_n))
    return LCL, xdb, UCL

LCL, xdb, UCL = shewhart_limits(
    subgroups_xbar, subgroups_S, N_sub)
(LCL, xdb, UCL)

# Any points outside these limits?
fig = pd.Series(subgroups_xbar).plot.line(
    title="Phase I subgroups: round 1")
fig.update_layout(
    xaxis_title_text="Sequence order",
    yaxis=dict(range=ylim))
fig.add_hline(y=UCL, line_color="red")
fig.add_hline(y=LCL, line_color="red")
fig.add_hline(y=xdb, line_color="green")
fig.show()

R, 77 lines

file <- 'https://openmv.net/file/gas-furnace.csv'
data <- read.csv(file)
CO2 <- data$CO2
N.raw <- length(CO2)
N.sub <- 6

# Change ``N.sub`` to 10, 15, 20, etc
# At N.sub <- 17 we see the
# autocorrelation disappear

# Plot all the data
par(mar=c(4.2, 4.2, 0.5, 0.5))
par(cex.lab=1.3, cex.main=1.5,
    cex.sub=1.5, cex.axis=1.5)
plot(CO2, type="p", pch=".", cex=2,
     main="", ylab="CO2: raw data",
     xlab="Sequence order")

# Create the subgroups on ALL the raw data.
# Form a matrix with `N.subgroup` rows by
# placing the vector of data down each row,
# then going across to form the columns.
# Calculate the mean and standard deviation
# within each subgroup (columns of the matrix)

subgroups <- matrix(CO2, N.sub, N.raw/N.sub)
subgroups.S <- apply(subgroups, 2, sd)
subgroups.xbar <- apply(subgroups, 2, mean)
ylim <- range(subgroups.xbar) + c(-3, +3)

# Keep adjusting N.sub until you don't see
# any autocorrelation between subgroups
acf(subgroups.xbar)

# Create a function to calculate
# Shewhart chart limits
shewhart_limits <- function(xbar, S,
                        sub.n, N.stdev=3){
  # Give the xbar and S vector containing
  # the subgroup means and standard
  # deviations.  Also give the subgroup
  # size used. Returns the lower and upper
  # control limits for the Shewhart chart
  # (UCL and LCL) which are N.stdev away
  # from the target.

  # xdb = x.double.bar = mean of means
  xdb <- mean(xbar)
  s.bar <- mean(S)
  num.an <- sqrt(2)*gamma(sub.n/2)
  den.an <- sqrt(sub.n-1)*gamma((sub.n-1)/2)
  an <- num.an / den.an
  LCL <- xdb - 3*s.bar/(an*sqrt(sub.n))
  UCL <- xdb + 3*s.bar/(an*sqrt(sub.n))
  return(list(LCL, xdb, UCL))
}

limits <- shewhart_limits(subgroups.xbar,
                     subgroups.S, N.sub)
LCL <- limits[1]
xdb <- limits[2]
UCL <- limits[3]
c(LCL, xdb, UCL)

# Any points outside these limits?
par(mar=c(4.2, 4.2, 0.5, 0.5))
par(cex.lab=1.3, cex.main=1.5,
    cex.sub=1.5, cex.axis=1.5)
plot(subgroups.xbar, type="b", pch=".",
     cex=5, main="", ylim=ylim,
     ylab="Phase I subgroups: round 1",
     xlab="Sequence order")
abline(h=UCL, col="red")
abline(h=LCL, col="red")
abline(h=xdb, col="green")
lines(subgroups.xbar, type="b", pch=".",
      cex=5)

Question

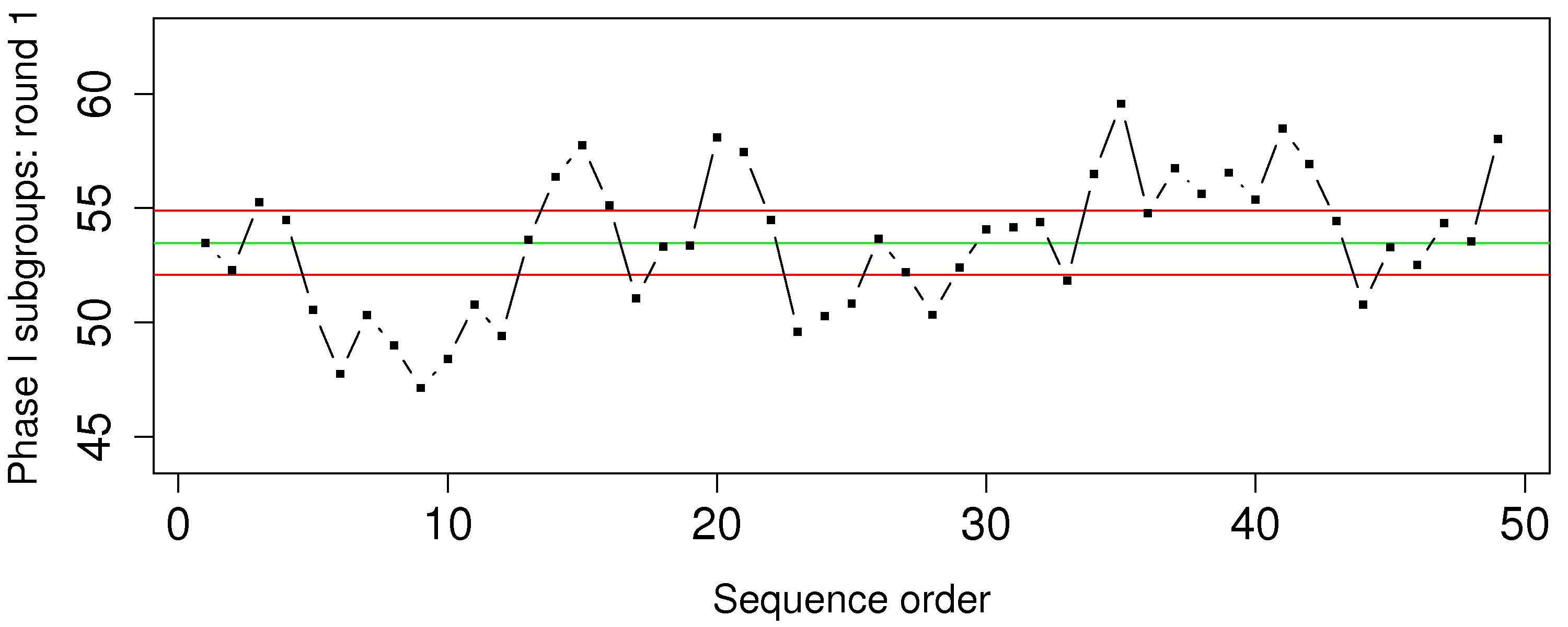
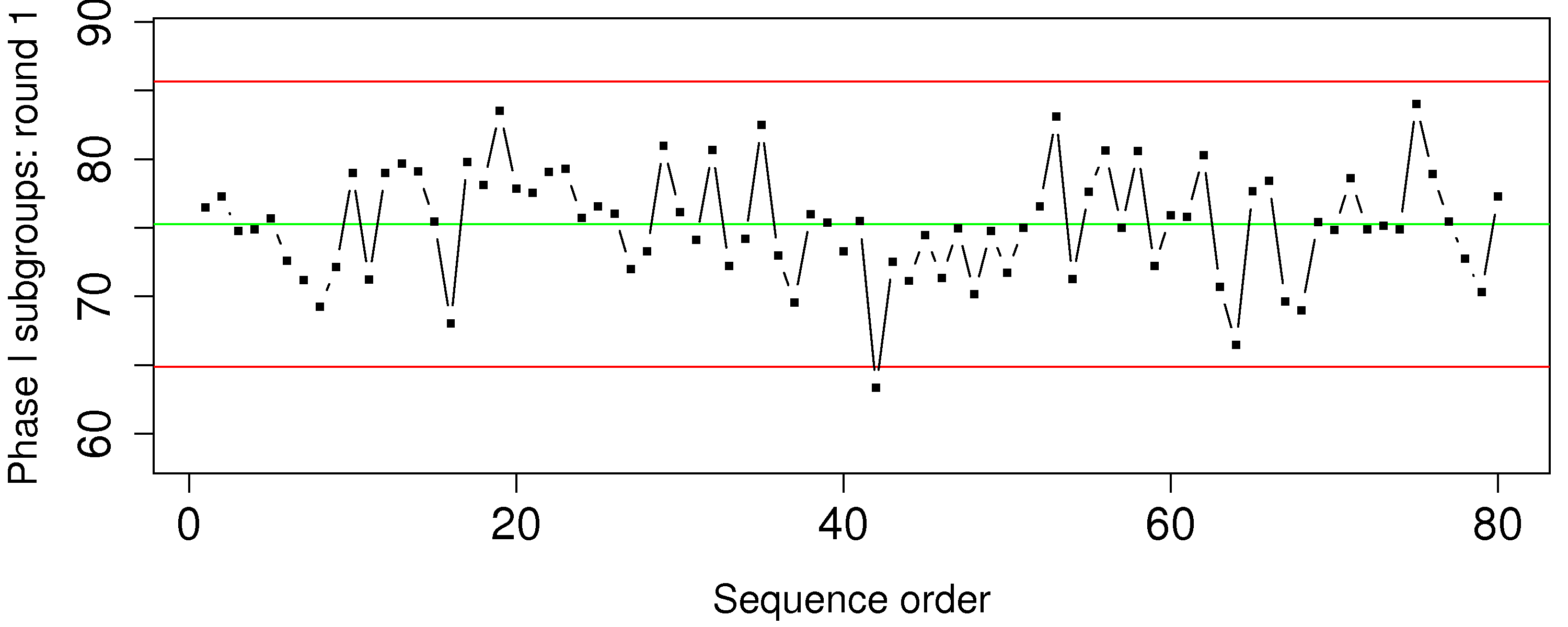
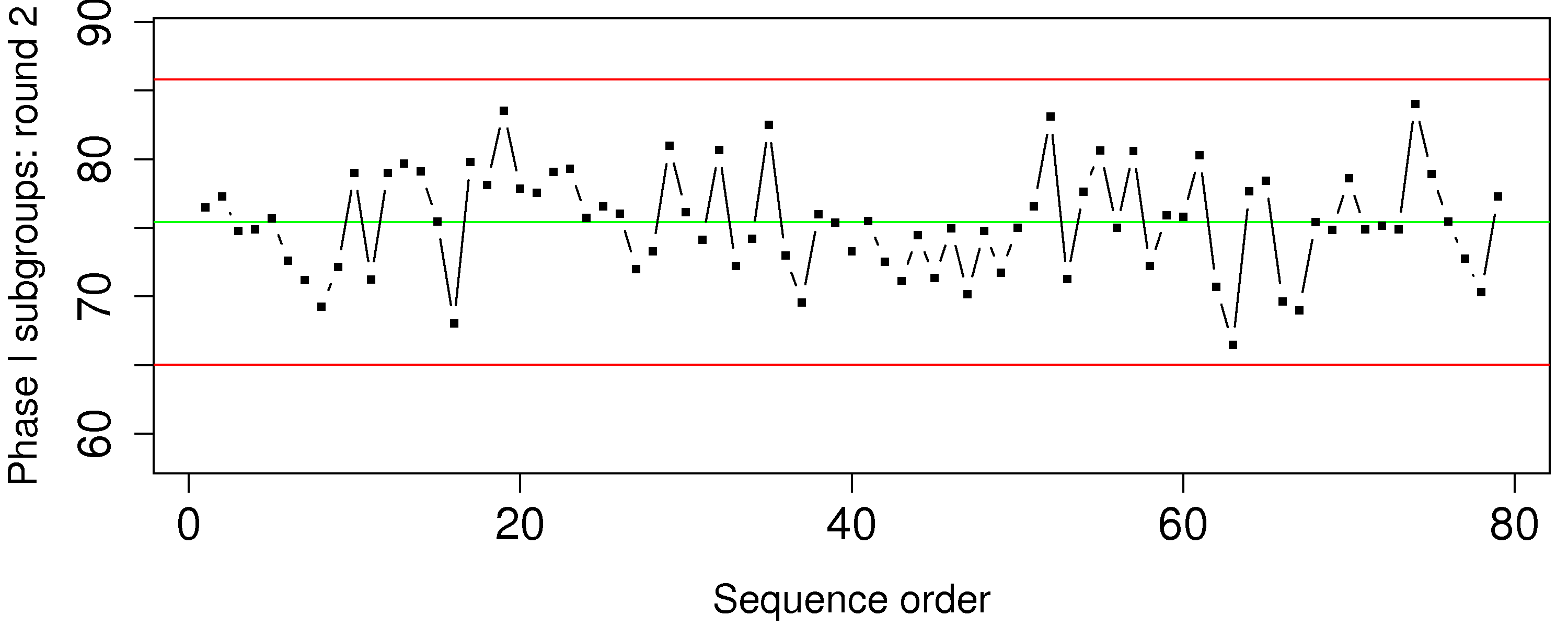
The percentage yield from a batch reactor, and the purity of the feedstock are available as the Batch yield and purity data set. Assume these data are from phase 1 operation and calculate the Shewhart chart upper and lower control limits that you would use during phase 2. Use a subgroup size of \(n=3\).

1. What is phase 1?

2. What is phase 2?

3. Show your calculations for the upper and lower control limits for the Shewhart chart on the yield value.

4. Show a plot of the Shewhart chart on these phase 1 data.

Solution

Solution based on work by Ryan McBride, Stuart Young, and Mudassir Rashid (2011 class)

1. Phase 1 is the period from which historical data is taken that is known to be “in control”. From this data, upper and lower control limits can be established for the monitored variable that contain a specified percent of all in control data.

2. Phase 2 is the period during which new, unseen data is collected by process monitoring in real-time. This data can be compared with the limits calculated from the “in control” data.

3. Assuming the dataset was derived from phase 1 operation, the batch yield data was grouped into subgroups of size 3. However, since the total number of data points (N=241) is not a multiple of three, the data set was truncated to the closest multiple of 3, i.e. \(N_{new} = 240\), by removing the last data point. Subsequently, the mean and standard deviation were calculated for each of the 80 subgroups. From this data, the lower and upper control limits were calculated as follows:

   \[\begin{split}\overline{\overline{x}} &= \frac{1}{80}\sum\limits_{k=1}^{80}\overline{x}_k = \bf{75.3}\\ \overline{S} &= \frac{1}{80}\sum\limits_{k=1}^{80}s_k = \bf{5.32}\\ \text{LCL} &= \overline{\overline{x}} - 3\cdot\frac{\overline{S}}{a_n\sqrt{n}} = \bf{64.9}\\ \text{UCL} &= \overline{\overline{x}} + 3\cdot\frac{\overline{S}}{a_n\sqrt{n}} = \bf{85.7}\\ \text{using}\,\,a_n &= 0.886\qquad \text{for a subgroup size of 3}\\ \text{and}\,\,\overline{\overline{x}} &= 75.3\end{split}\]

   Noticing that the mean for subgroup 42, \(\overline{x}_{42}=63.3\), falls below this LCL, the control limits were recalculated excluding this subgroup from phase 1 data (see R-code). Following this adjustment, the new control limits were calculated to be:

   • LCL = 65.0

   • UCL = 85.8

4. Shewhart charts for both rounds of the yield data (before and after removing the outlier):

   

Python, 61 lines

import numpy as np
import pandas as pd
from scipy.special import gamma

pd.options.plotting.backend = "plotly"

# Recursively calculate the Shewhart limits,
# trimming subgroups outside the limits each
# round, until no more points are excluded.
file = ("https://openmv.net/file/"
        "batch-yield-and-purity.csv")
data = pd.read_csv(file)
y = data["yield"].to_numpy()
variable = "Yield"
N = 3

# No further changes required. The code
# below will work for any new data set.
# Truncate to the closest multiple of N
# so the reshape works.
y = y[: (len(y) // N) * N]
subgroups = y.reshape(len(y) // N, N).T
x_mean = subgroups.mean(axis=0)
x_sd = subgroups.std(axis=0, ddof=1)
ylim = (x_mean.min() - 5, x_mean.max() + 5)

num_an = np.sqrt(2) * gamma(N / 2)
den_an = np.sqrt(N - 1) * gamma((N - 1) / 2)
an = num_an / den_an

k = 1
doloop = True
# Prevent infinite loops.
while doloop and k < 5:
    S = x_sd.mean()
    xdb = x_mean.mean()  # x-double-bar
    LCL = xdb - (3 * S / (an * np.sqrt(N)))
    UCL = xdb + (3 * S / (an * np.sqrt(N)))
    print((LCL, UCL))

    fig = pd.Series(x_mean).plot.line(
        title=f"Phase I subgroups: round {k}")
    fig.update_layout(
        xaxis_title_text="Sequence order",
        yaxis=dict(range=ylim))
    fig.add_hline(y=UCL, line_color="red")
    fig.add_hline(y=LCL, line_color="red")
    fig.add_hline(y=xdb, line_color="green")
    fig.show()

    if not ((x_mean < LCL).any()
            or (x_mean > UCL).any()):
        # Finally! No more points to exclude.
        doloop = False
    k += 1

    # Keep only subgroups whose mean falls
    # inside the current control limits.
    keep = (x_mean >= LCL) & (x_mean <= UCL)
    x_sd = x_sd[keep]
    x_mean = x_mean[keep]

R, 64 lines

# Thanks to Mudassir for his source code to
# recursively calculate the limits. Some
# updates were made.

file <- 'https://openmv.net/file/batch-yield-and-purity.csv'
data <- read.csv(file)
y <- data$yield
variable <- "Yield"
N <- 3

# No further changes required. The code
# below will work for any new data set
subgroups <- matrix(y, N, length(y)/N)
x.mean <- numeric(length(y)/N)
x.sd <- numeric(length(y)/N)

# Calculate mean and sd of subgroups
# (see R-tutorial)
x.mean <- apply(subgroups, 2, mean)
x.sd <- apply(subgroups, 2, sd)
ylim <- range(x.mean) + c(-5, +5)
k <- 1
doloop <- TRUE

# Prevent infinite loops
while (doloop & k < 5){

  num.an <- sqrt(2)*gamma(N/2)
  den.an <- sqrt(N-1)*gamma((N-1)/2)
  an <- num.an / den.an

  S <- mean(x.sd)
  xdb <- mean(x.mean) # x-double bar
  LCL <- xdb - (3*S/(an*sqrt(N)))
  UCL <- xdb + (3*S/(an*sqrt(N)))
  print(c(LCL, UCL))

  # Create a figure on every loop
  par(mar=c(4.2, 4.2, 0.5, 0.5))
  par(cex.lab=1.3, cex.main=1.5,
      cex.sub=1.5, cex.axis=1.5)
  plot(x.mean, type="b", pch=".",
       cex=5, main="",
  ylab=paste("Phase I subgroups: round", k),
       xlab="Sequence order", ylim=ylim)
  abline(h=UCL, col="red")
  abline(h=LCL, col="red")
  abline(h=xdb, col="green")
  lines(x.mean, type="b", pch=".", cex=5)

  if (!(any(x.mean < LCL) | any(x.mean > UCL))){
    # Finally!  No more points to exclude
    doloop <- FALSE
  }
  k <- k + 1

  # Retain in x.sd and x.mean only those
  # entries that are within the control
  # limits
  x.sd <- x.sd[x.mean>=LCL]
  x.mean <- x.mean[x.mean>=LCL]
  x.sd <- x.sd[x.mean<=UCL]
  x.mean <- x.mean[x.mean<=UCL]
} # end: while doloop

Question

You will hear about 6-sigma processes frequently in your career. What does it mean exactly that a process is “6-sigma capable”? Draw a diagram to help illustrate your answer.