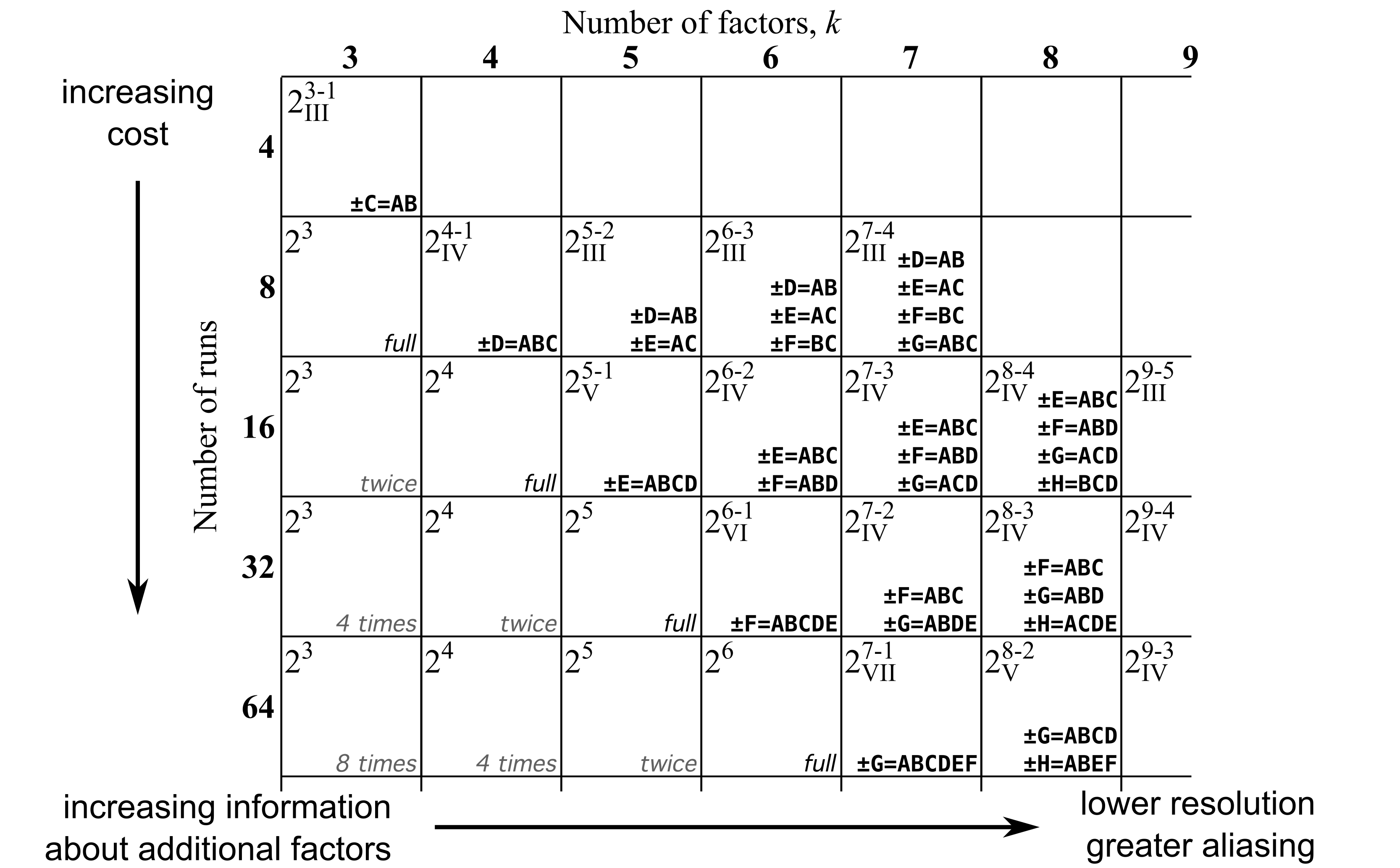
5.9.7. Design resolution

The resolution of a design is given by the length of the shortest word in the defining relation. We normally write the resolution as a subscript to the factorial design using Roman numerals. Some examples:

1. The \(2^{7-4}\) example 1 in the previous section had the shortest word of 3 characters, so this would be called a \(2^{7-4}_\text{III}\) design. Main effects were confounded with 2-factor interactions in that example.

2. The \(2^{8-4}\) example 2 had as the shortest word length of 4 characters, so this would be a \(2^{8-4}_\text{IV}\) design. Main effects were confounded with 3-factor interactions.

3. Finally, imagine the case of \(2^{5-1}\), in other words a half-fraction design. The first four factors are written in the standard factorial way, but the fifth factor is generated from E = ABCD. So its defining relation is I = ABCDE, where the shortest word, not counting the intercept, is 5 characters - it is a \(2^{5-1}_{\text{V}}\) design. You can verify for yourself that main effects will be confounded with 4-factor interactions in this design.

You can consider the resolution of a design to be an indication of how clearly the effects can be separated in a design. The higher the resolution, the lower the degree of confounding: this is desirable. Within reason, always aim for a higher resolution design given your experimental budget, but also accept a lower resolution, at least initially, in order to test for more factors. We will discuss this further in the section on screening designs.

You can interpret the resolution index as follows: let main effects = 1, two-factor interactions = 2, three-factor interactions = 3, etc. Then subtract this number from the resolution index to show how that effect is aliased. Consider a resolution IV design, since \(4-1=3\), it indicates that main effects are aliased with 3fi, but not with two-factor interactions; and \(4-2 = 2\) indicates that 2fi are aliased with each other. Here is a summary:

Resolution III designs: are good for screening

• Are excellent for initial screening: to separate out the important factors from the many potential factors. To identify important variables that can be studied in the next experiments.

• Main effects are not confounded with each other.

• Main effects are aliased with two-factor interactions (\(3 - 1 = 2\)).

• Two-factor interactions are aliased with main effects (\(3 - 2 = 1\)).

Resolution IV designs: are good for characterizing

• Most useful for characterizing (learning about and understanding) a system, both the main effects and the interactions, since:

• Interactions are very interesting in many systems, since they go beyond just the main effects and can improve your process even more (or sometimes take away from it too!).

• Main effects are not confounded with each other.

• Main effects are not aliased with two-factor interactions either (\(4-1=3\)).

• Main effects are aliased with three-factor interactions though (\(4-1=3\)).

• Two-factor interactions are still aliased with each other though (\(4-2=2\)).

Resolution V designs: are good for optimizing

• For optimizing a process, learning about complex effects, and developing high-accuracy predictive models, since:

• Main effects are not confounded with each other.

• Main effects are not aliased with two-factor interactions.

• Two-factor interactions are not aliased with each other either.

• But two-factor interactions are aliased with three-factor interactions (\(5-2=3\)).

The above guidance about using resolution IV and V designs for characterization and optimization is fairly general - there are many cases where a satisfactory optimization can be performed with a resolution IV experiment.

In this text currently, for resolution III, IV and V designs we look at factorial designs. However, there are a number of other design types which can also be used. If you are interested, please research Plackett-Burman designs, Box-Behnken designs, central composite designs, and definitive screening designs.

You can use the following table to visualize the trade-off between design resolution, the number of factors (\(k\)), the number of runs required, and the aliasing pattern. The table is adapted from the text by Box, Hunter and Hunter (2nd edition, p 272), and (1st edition, p 410).

5.9.7.1. Generating the trade-off table

The table is also computed, rather than read off the page, by process_improve. The generators in each cell are found by an exhaustive minimum-aberration search: for every candidate set of generators the defining relation is worked out, the lengths of its words are counted, and the set that has the fewest short words is kept. Nothing is looked up from a catalogue, and the cells agree with the printed table.

Python, 4 lines

from process_improve.experiments import get_trade_off_table_entry, trade_off_table

trade_off_table()                                       # the whole table
get_trade_off_table_entry(n_runs=16, n_factors=7)       # one cell, with its alias chains

Run in browser

Two things follow from having the table as code rather than as an image. The first is that it can be widened past the edge of a printed page: trade_off_table(runs=(8, 16, 32), factors=range(3, 12)) carries it out to eleven factors. The second is that a single cell can be asked for its details, which the image can only summarise as a resolution:

Output, 14 lines

With 16 experiments, and 7 factors:
  Design: 2^(7-3) IV
  Resolution: IV
  Generators:
      E=ABC
      F=ABD
      G=ACD
      (each generator may be used with a + or a - sign)
  Aliasing (main effects and 2-factor interactions only):
      Main effects are not aliased with 2-factor interactions.
      A = BCE + BDF + CDG + EFG + ABCFG + ABDEG + ACDEF
      ...
      AB = CE + DF + ACFG + ADEG + BCDG + BEFG + ABCDEF
      ...

Read those two alias chains against the resolution. This is a \(2^{7-3}_\text{IV}\) design, so \(4 - 1 = 3\) says the main effect A is aliased with three-factor interactions and not with any two-factor interaction, which is what the report prints; and \(4 - 2 = 2\) says the two-factor interactions are aliased with each other, which is why the chain for AB opens with CE and DF. Passing display=False returns the same information as an object whose fields (label, resolution, generators, defining_relation, aliases) can be read in code.