6.5.18. Latent variable contribution plots¶
We have previously seen how contribution plots are constructed for a score value, for the SPE and for
There are
The contribution to
For SPE =
The SPE contributions are usually shown as the square of the values in brackets, accounting for the sign, as in
The other point to mention here is that contributions are calculated from one point to another point. Most often, the from point is the model center or the model plane. So for SPE, the contributions are from the model plane to the
But sometimes we would like to know, as in the figure below, what are the contribution from one point to another. And these start and end points need not be an actual point; for a group of points we can use a suitable average of the points in the cluster. So there are point-to-point, point-to-group, group-to-point, and group-to-group contributions in the scores.
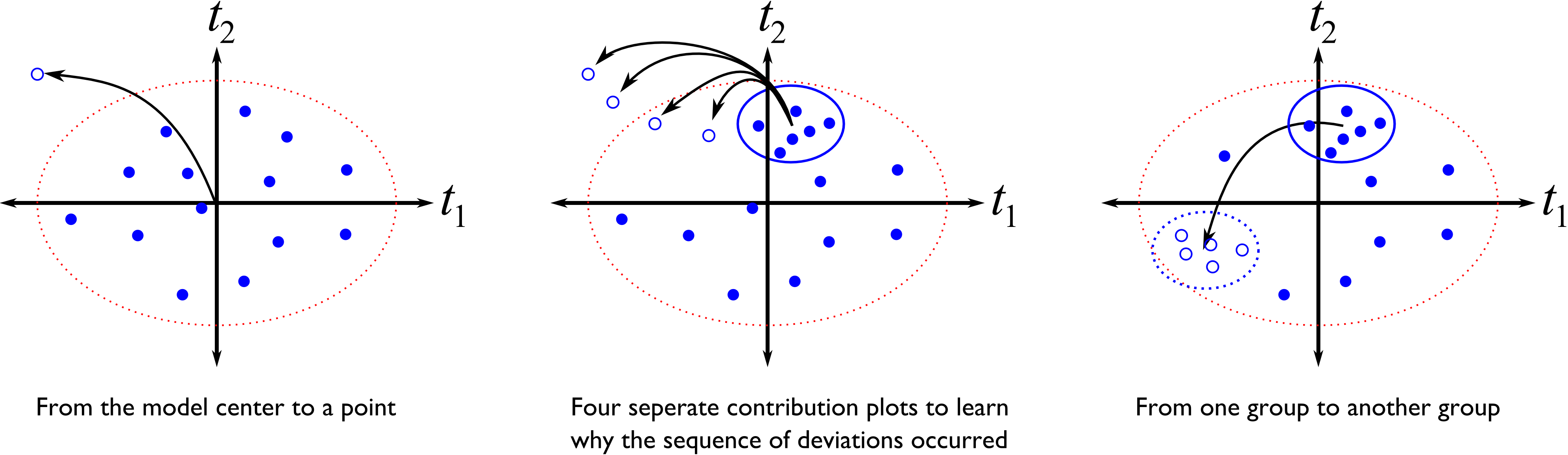
The calculation procedure is actually the same in all cases: for a group of points, collapse it down to the center point in the group, then calculate the point-to-point contribution. If the starting point is not specified, then the contribution will be from the model center, i.e.