3.4. Shewhart charts

A Shewhart chart, named after Walter Shewhart from Bell Telephone and Western Electric, monitors that a process variable remains on target and within given upper and lower limits. It is a monitoring chart for location. It answers the question whether the variable’s location is stable over time. It does not track anything else about the measurement, such as its standard deviation. Looking ahead: we show later that a pure Shewhart chart needs extra rules to help monitor the location of a variable effectively.

The defining characteristics of a Shewhart chart are: a target, upper and lower control limits (UCL and LCL). These action limits are defined so that no action is required as long as the variable plotted remains within the limits. In other words a special cause is not likely present if the points remain within the UCL and LCL.

3.4.1. Derivation using theoretical parameters

Define the variable of interest as \(x\), and assume that we have samples of \(x\) available in sequence order. No assumption is made regarding the distribution of \(x\). The average of \(n\) of these \(x\)-values is defined as \(\overline{x}\), which from the Central limit theorem we know will be more normally distributed with unknown population mean \(\mu\) and unknown population variance \(\sigma^2/n\), where \(\mu\) and \(\sigma\) refer to the distribution that samples of \(x\) came from. The figure here shows the case for \(n=5\). This normal approximation for \(\overline{x}\) improves as \(n\) grows; for small subgroups drawn from a strongly skewed distribution it is weaker, and the nominal false-alarm rate derived below should then be read as approximate.

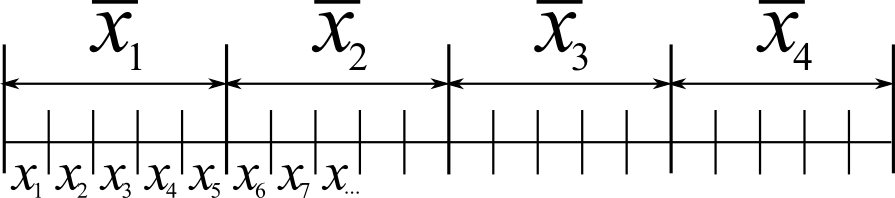
So by taking subgroups of size \(n\) values, we now have for each subgroup a newly calculated variable, \(\overline{x}\) and we will define a shorthand symbol for its standard deviation: \(\sigma_{\overline{X}} = \sigma/\sqrt{n}\). Writing a \(z\)-value for \(\overline{x}\), and its associated confidence interval for \(\mu\) is now easy after studying the section on confidence intervals:

\[z = \frac{\displaystyle \overline{x} - \mu}{\displaystyle \sigma_{\overline{X}}}\]

Assuming we know \(\sigma_{\overline{X}}\), which we usually do not in practice, we can invoke the normal distribution and calculate the probability of finding a value of \(z\) between \(c_n = -3\) to \(c_n = +3\):

(1)\[\begin{split}\begin{array}{rcccl} - c_n &\leq& \dfrac{\overline{x} - \mu}{\sigma_{\overline{X}}} &\leq& +c_n\\ \\ \overline{x} - c_n\sigma_{\overline{X}} &\leq& \mu &\leq& \overline{x} + c_n\sigma_{\overline{X}} \\ \\ \text{LCL} &\leq& \mu &\leq& \text{UCL} \end{array}\end{split}\]

The reason for \(c_n = \pm 3\) is that the total area between that lower and upper bound spans 99.73% of the area (in R: pnorm(+3) - pnorm(-3) gives 0.9973). So it is highly unlikely, a chance of 1 in 370, that a data point, \(\overline{x}\), calculated from a subgroup of \(n\) raw \(x\)-values, will lie outside these bounds.

The algebra above is written as an interval that brackets \(\mu\), but in operation the centre line is held fixed (at the target, or at \(\overline{\overline{x}}\) once it is estimated) and these same limits are used to bracket each newly plotted \(\overline{x}\). The two views give the identical LCL and UCL because the interval is symmetric about the centre.

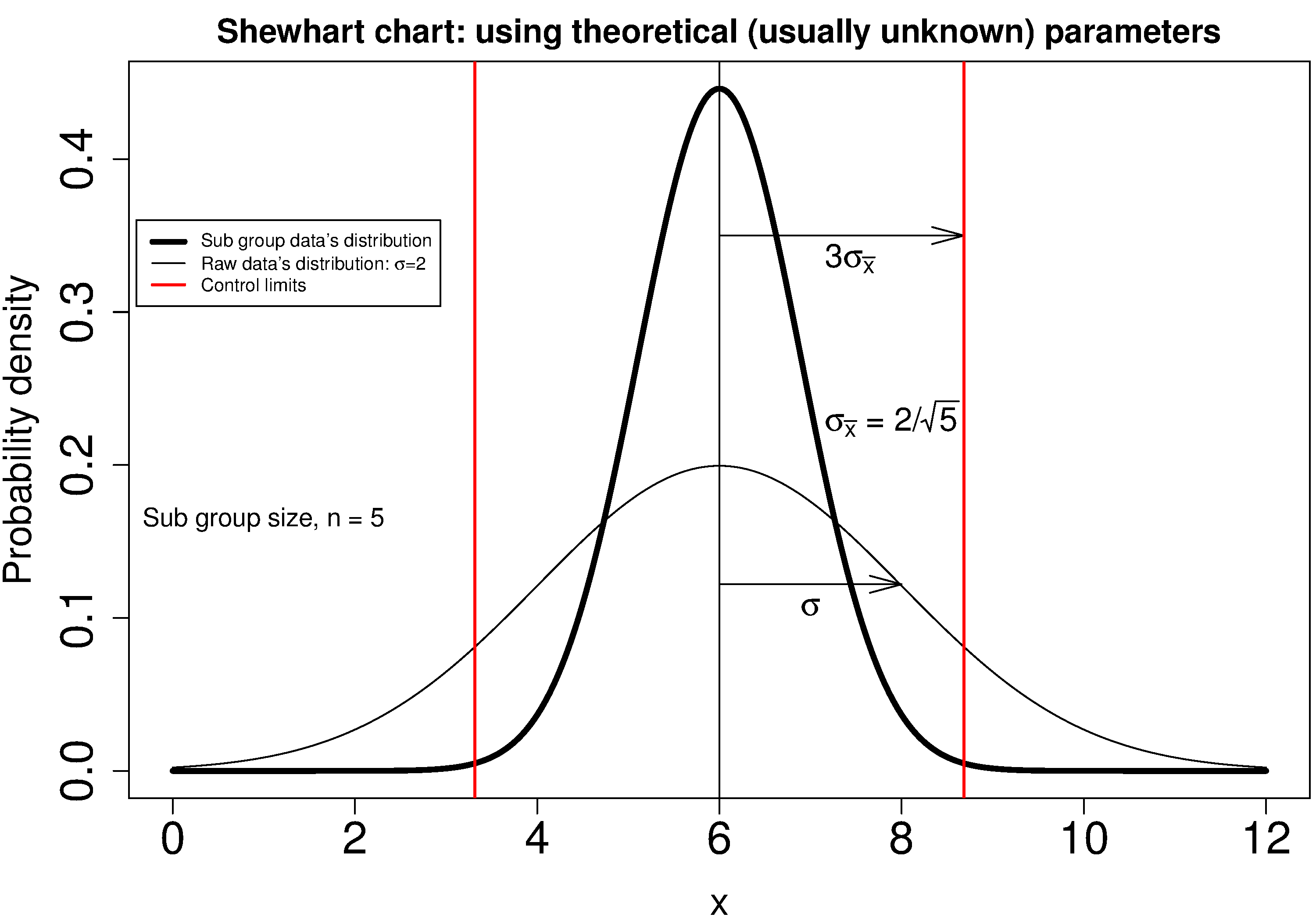
The following illustration should help connect the concepts: the raw data’s distribution happens to have a mean of 6 and standard deviation of 2, while it is clear the distribution of the subgroups of 5 samples (thicker line) is much narrower.

Python, 17 lines

import numpy as np
import plotly.graph_objects as go
from scipy.stats import norm

# The raw data distribution, and the distribution of
# subgroup averages (n = 5), which is narrower by sqrt(n).
raw_mean, raw_sd, n = 6, 2, 5
sub_sd = raw_sd / np.sqrt(n)
x = np.linspace(raw_mean - 4 * raw_sd, raw_mean + 4 * raw_sd, 500)

fig = go.Figure()
fig.add_trace(go.Scatter(x=x, y=norm.pdf(x, raw_mean, raw_sd),
                         name="raw data, x"))
fig.add_trace(go.Scatter(x=x, y=norm.pdf(x, raw_mean, sub_sd),
                         name="subgroup average (n=5)"))
fig.update_layout(xaxis_title="x", yaxis_title="Probability density")
fig.show()

3.4.2. Using estimated parameters instead

The derivation in equation (1) requires knowing the population standard deviation, \(\sigma\), and assuming that our target for \(x\) is \(\mu\). The latter assumption is reasonable, but we will estimate a value for \(\sigma\) instead, using the data.

Let’s take a look at phase 1, the step where we are building the monitoring chart’s limits from historical data. Create a new variable \(\overline{\overline{x}}\) \(= \displaystyle \frac{1}{K} \sum_{k=1}^{K}{ \overline{x}_k}\), where \(K\) is the number of \(\overline{x}\) samples we have available to build the monitoring chart, called the phase 1 data. Note that \(\overline{\overline{x}}\) is sometimes called the grand mean. Alternatively, just set \(\overline{\overline{x}}\) to the desired target value for \(x\) or use a long portion of stable data to estimate a suitable target

The next hurdle is \(\sigma\). Define \(s_k\) to be the standard deviation of the \(n\) values in the \(k^\text{th}\) subgroup. We do not show it here, but for a subgroup of \(n\) samples, an unbiased estimator of \(\sigma\) is given by \(\displaystyle \frac{\overline{S}}{a_n}\), where \(\overline{S} = \displaystyle \frac{1}{K} \displaystyle \sum_{k=1}^{K}{s_k}\) is simply the average standard deviation calculated from \(K\) subgroups. Values for \(a_n\) are looked up from a table, or using the formula below, and depend on the number of samples we use within each subgroup.

\(n\)	2	3	4	5	6	7	8	10	15
\(a_n\)	0.7979	0.8862	0.9213	0.9400	0.9515	0.9594	0.9650	0.9727	0.9823

More generally, using the \(\Gamma(...)\) function, for example gamma(...) in R or MATLAB, or math.gamma(...) in Python, you can reproduce the above \(a_n\) values.

\[a_n = \frac{\sqrt{2}\,\,\Gamma(n/2)}{\sqrt{n-1}\,\,\Gamma(n/2 - 0.5)}\]

Notice how the \(a_n\) values tend to 1.0 the larger the subgroup size, indicating we need less of a correction to make the standard deviation less biased. Once we have this unbiased estimator for the standard deviation from these \(K\) subgroups, we can write down suitable lower and upper control limits for the Shewhart chart:

(2)\[\begin{array}{rcccl} \text{LCL} = \overline{\overline{x}} - 3 \cdot \frac{\displaystyle \overline{S}}{\displaystyle a_n\sqrt{n}} && && \text{UCL} = \overline{\overline{x}} + 3 \cdot \frac{\displaystyle \overline{S}}{\displaystyle a_n\sqrt{n}} \end{array}\]

It is highly unlikely that all the data chosen to calculate the phase 1 limits actually lie within these calculated LCL and UCLs. Those portions of data not from stable operation, which are outside the limits, should not have been used to calculate these limits. Those unstable data bias the limits to be wider than required.

Exclude these outlier data points and recompute the LCL and UCLs. Usually this process is repeated 2 to 3 times. It is wise to investigate the data being excluded to ensure they truly are from unstable operation. If they are from stable operation, then they should not be excluded. These data may be violating the assumption of independence. One may consider using wider limits, or use an EWMA control chart.

Example

Bales of rubber are being produced, with every 10th bale automatically removed from the line for testing. Measurements of colour intensity are made on 5 sides of that bale, using calibrated digital cameras under controlled lighting conditions. The rubber compound is used for medical devices, so it needs to have the correct colour, as measured on a scale from 0 to 255. The average of the 5 colour measurements is to be plotted on a Shewhart chart. So we have a new data point appearing on the monitoring chart after every 10th bale.

In the above example the raw data are the bale’s colour. There are \(n = 5\) values in each subgroup. Collect say \(K=20\) samples of good production bales considered to be from stable operation. No special process events occurred while these bales were manufactured.

The data below represent the average of the \(n=5\) samples from each bale, there are \(K=20\) of these subgroups.

\[\overline{x} = [245, 239, 239, 241, 241, 241, 238, 238, 236, 248, 233, 236, 246, 253, 227, 231, 237, 228, 239, 240]\]

The overall average is \(\overline{\overline{x}} = 238.8\) and \(\overline{S} = 9.28\). The raw data are available on this website and you can verify the values of \(\overline{\overline{x}}\) and \(\overline{S}\) were correctly calculated.

• Calculate the lower and upper control limits for this Shewhart chart.

• Were there any points in the phase 1 data (training phase) that exceeded these limits?

  • LCL = \(\overline{\overline{x}} - 3 \cdot \frac{\displaystyle \overline{S}}{\displaystyle a_n\sqrt{n}} = 238.8 - 3 \cdot \displaystyle \frac{9.28}{(0.94)(\sqrt{5})} = 225.6\)

  • UCL = \(\overline{\overline{x}} + 3 \cdot \frac{\displaystyle \overline{S}}{\displaystyle a_n\sqrt{n}} = 238.8 + 3 \cdot \displaystyle \frac{9.28}{(0.94)(\sqrt{5})} = 252.0\)

  • The group with \(\overline{x}\) = 253 exceeds the calculated upper control limit.

  • That \(\overline{x}\) point should be excluded and the limits recomputed. You can show the new \(\overline{\overline{x}} = 238.0\) and \(\overline{S} = 9.68\) and the new LCL = 224 and UCL = 252.

In source code:

Python, 51 lines

import numpy as np
from scipy.special import gamma

# Given information (but calculate yourself
# from https://openmv.net/info/rubber-colour)
xbar = np.array([245, 239, 239, 241, 241, 241, 238,
                 238, 236, 248, 233, 236, 246, 253,
                 227, 231, 237, 228, 239, 240],
                dtype=float)

# Number of measurements per subgroup
N_sub = 5

# Average of the 20 standard deviations
# of the 20 subgroups
S = 9.28

# xdb = x double bar = overall mean =
#       mean of the means
xdb = xbar.mean()

num_an = np.sqrt(2) * gamma(N_sub / 2)
den_an = np.sqrt(N_sub - 1) * gamma((N_sub - 1) / 2)
an = num_an / den_an

LCL = xdb - (3 * S / (an * np.sqrt(N_sub)))
UCL = xdb + (3 * S / (an * np.sqrt(N_sub)))
print(f"Control limits: [{round(LCL, 2)}; "
      f"{round(UCL, 2)}]")

print(f"Number > UCL: {(xbar > UCL).sum()}")
print(f"Number < LCL: {(xbar < LCL).sum()}")

# Exclude the one subgroup above the UCL.
# Do this by setting it to NaN (missing).
xbar[xbar > UCL] = np.nan

# Calculate the mean, ignoring NaN.
xdb = np.nanmean(xbar)

# 'S' will change also. If you download the
# raw data (link above), you can prove
# that the new 'S' will be:
S = 9.68

# 'an' and N_sub will not change.

LCL = xdb - (3 * S / (an * np.sqrt(N_sub)))
UCL = xdb + (3 * S / (an * np.sqrt(N_sub)))
print(f"Control limits: [{round(LCL)}; "
      f"{round(UCL)}]")

R, 48 lines

# Given information (but calculate yourself
# from https://openmv.net/info/rubber-colour)
xbar = c(245, 239, 239, 241, 241, 241, 238,
         238, 236, 248, 233, 236, 246, 253,
         227, 231, 237, 228, 239, 240)

# Number of measurements per subgroup
N.sub = 5

# Average of the 20 standard deviations
# of the 20 subgroups
S = 9.28

# xdb = x double bar = overall mean =
#       mean of the means
xdb = mean(xbar)

num.an = sqrt(2) * gamma(N.sub/2)
den.an = sqrt(N.sub-1) * gamma((N.sub-1)/2)
an = num.an / den.an

LCL = xdb - (3 * S/(an * sqrt(N.sub)))
UCL = xdb + (3 * S/(an * sqrt(N.sub)))
paste0('Control limits: [', round(LCL, 2),
       '; ', round(UCL,2), ']')

paste0('Number > UCL: ', sum(xbar > UCL))
paste0('Number < LCL: ', sum(xbar < LCL))

# Exclude the one subgroup above the UCL.
# Do this by setting it to 'NA' (missing)
xbar[xbar > UCL] = NA

# Calculate the mean, removing missing
# values (ignore it).
xdb = mean(xbar, na.rm=TRUE)

# 'S' will change also. If you download the
# raw data (link above), you can prove
# that the new 'S' will be:
S = 9.68

# The 'an' and 'N.sub' will not change.

LCL = xdb - (3 * S/(an * sqrt(N.sub)))
UCL = xdb + (3 * S/(an * sqrt(N.sub)))
paste0('Control limits: [', round(LCL, 0),
       '; ', round(UCL,0), ']')

3.4.3. Phase 1 versus phase 2 in this example

The rubber-bale calculation above is entirely phase 1: we used a batch of historical subgroups to estimate where the chart’s limits should sit. The steps were:

1. collect \(K=20\) subgroups believed to be from stable operation;

2. compute the grand mean \(\overline{\overline{x}}\) and the average subgroup standard deviation \(\overline{S}\), giving a first set of limits, [225.6, 252.0];

3. notice the subgroup with \(\overline{x}=253\) lies above the UCL, exclude it, and recompute, arriving at the final limits, [224, 252].

Nothing has been monitored yet. Phase 1 answers only the question “where should the limits sit?”.

Phase 2 begins once those limits are frozen. Each new subgroup average, as its bale is tested, is plotted against the fixed centre line and the fixed [224, 252] limits; no limit is recomputed. A point outside the limits raises a signal. Suppose the next six bales give subgroup averages of 242, 236, 248, 254, 240, and 233. Only the fourth, \(\overline{x}=254\), lies above the UCL of 252, so the chart signals on that bale and the operator investigates.

Python, 10 lines

# Phase 1 produced these frozen limits:
LCL, UCL = 224.0, 252.0

# Phase 2: plot each new subgroup average against
# the frozen limits and flag any that fall outside.
new_xbar = np.array([242, 236, 248, 254, 240, 233])
signals = (new_xbar > UCL) | (new_xbar < LCL)
for k, (value, flag) in enumerate(zip(new_xbar, signals), start=1):
    state = "SIGNAL" if flag else "in control"
    print(f"Bale {k}: xbar={value} -> {state}")

The limits are calculated once, in phase 1, and then held fixed throughout phase 2. Re-estimating them from the phase 2 data as it arrives would let a slow drift quietly widen the limits and hide the very problem you are trying to detect.

3.4.4. Judging the chart’s performance

There are 2 ways to judge performance of a monitoring chart. In particular here we discuss the Shewhart chart:

1. Error probability.

We define two types of errors, Type I and Type II, which are a function of the lower and upper control limits (LCL and UCL).

You make a type I error when your sample is typical of normal operation, yet, it falls outside the UCL or LCL limits. We showed in the theoretical derivation that the area covered by the upper and lower control limits is 99.73%. The probability of making a type I error, usually denoted as \(\alpha\) is then \(100 - 99.73 = 0.27\%\).

Synonyms for a type I error: false alarm, false positive (used mainly for testing of diseases), producer’s risk (used for acceptance sampling, because here as the producer you will be rejecting an acceptable sample), false rejection rate, or alpha.

You make a type II error when your sample really is abnormal, but falls within the UCL and LCL limits and is therefore not detected. This error rate is denoted by \(\beta\), and it is a function of the degree of abnormality, which we derive next.

Synonyms for a type II error: false negative (used mainly for testing of diseases), consumer’s risk (used for acceptance sampling, because your consumer will be receiving available product which is defective), false acceptance rate, or beta.

To quantify the probability \(\beta\), recall that a Shewhart chart is for monitoring location, so we make an assumption that the new, abnormal sample comes from a distribution which has shifted its location from \(\mu\) to \(\mu + \Delta\sigma\) (e.g. \(\Delta\) can be positive or negative). Now, what is the probability this new sample, which come from the shifted distribution, will fall within the existing LCL and UCL? This figure shows the probability is \(\beta = (1 - \text{the shaded area})\).

\[\begin{split}\alpha &= Pr\left(\overline{x}\,\,\text{is in control, but lies outside the limits}\right) = \text{type I error rate}\\ \beta &= Pr\left(\overline{x}\,\,\text{is not in control, but lies inside the limits}\right) = \text{type II error rate}\end{split}\]

Python, 21 lines

# Type II error: the probability a shifted subgroup mean still
# lands inside the limits. Working in units of the raw sigma,
# with n = 4 and a shift of delta = 1 sigma.
n, delta = 4, 1.0
se = 1 / np.sqrt(n)              # standard error of xbar, in sigma units
LCL, UCL = -3 * se, 3 * se       # limits around the in-control mean of 0
beta = norm.cdf(UCL, delta, se) - norm.cdf(LCL, delta, se)
print(f"beta = {beta:.4f} for a {delta} sigma shift, n = {n}")

x = np.linspace(-4 * se, delta + 4 * se, 600)
fig = go.Figure()
fig.add_trace(go.Scatter(x=x, y=norm.pdf(x, 0, se), name="in control"))
fig.add_trace(go.Scatter(x=x, y=norm.pdf(x, delta, se), name="shifted"))
# Shade the beta region: the shifted curve between the limits.
mask = (x >= LCL) & (x <= UCL)
fig.add_trace(go.Scatter(x=x[mask], y=norm.pdf(x[mask], delta, se),
                         fill="tozeroy", mode="none",
                         fillcolor="rgba(0,0,200,0.3)", name="beta"))
for limit in (LCL, UCL):
    fig.add_vline(x=limit, line_dash="dash")
fig.show()

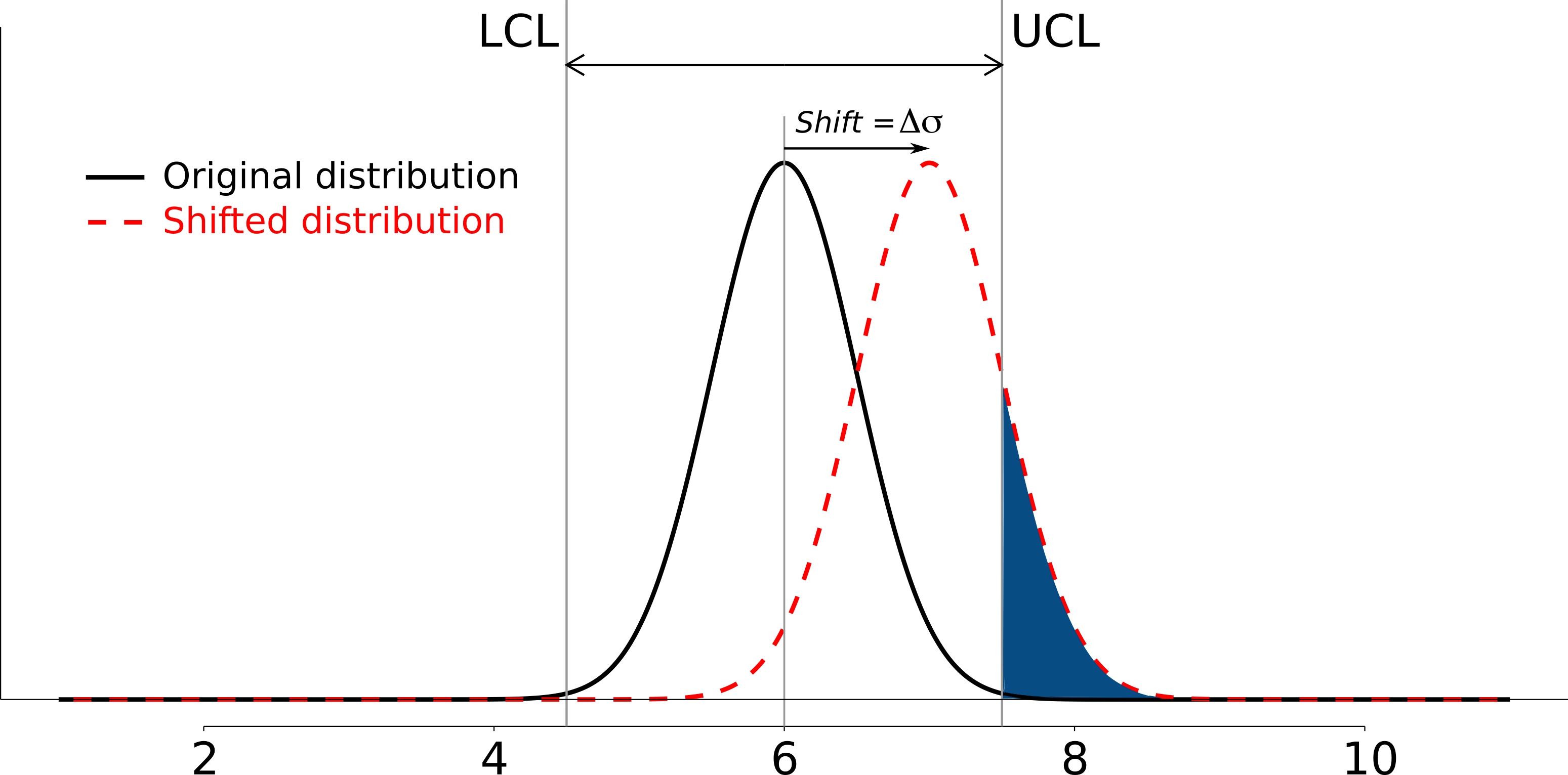
The table highlights that \(\beta\) is a function of the amount by which the process shifts = \(\Delta\), where \(\Delta=1\) implies the process has shifted up by \(1\sigma\). The table was calculated for \(n=4\) and used critical limits of \(\pm 3 \sigma_{\overline{X}}\). You can calculate your own values of \(\beta\) using this line of R code: beta <- pnorm(3 - delta*sqrt(n)) - pnorm(-3 - delta*sqrt(n))

\(\Delta\)	0.25	0.50	0.75	1.00	1.50	2.00
\(\beta\) when \(n=4\)	0.9936	0.9772	0.9332	0.8413	0.5000	0.1587

Python, 10 lines

import numpy as np
from scipy.stats import norm

delta = 1
n = 4
beta = (norm.cdf(+3 - delta * np.sqrt(n))
        - norm.cdf(-3 - delta * np.sqrt(n)))

print(f"When delta={delta} and n={n} "
      f"then beta = {round(beta, 4)}")

R, 7 lines

delta <- 1
n <- 4
beta <- pnorm(+3 - delta*sqrt(n)) -
        pnorm(-3 - delta*sqrt(n))

paste0('When delta=', delta, ' and n=', n,
       ' then beta = ', round(beta, 4))

The key point you should note from the table is that a Shewhart chart is not good (it is slow) at detecting a change in the location (level) of a variable. This is surprising given the intention of the plot is to monitor the variable’s location. Even a moderate shift of \(0.75\sigma\) units \((\Delta=0.75)\) will only be detected around 6.7% of the time (\(100-93.3\%\)) when \(n=4\). That 6.7% is the chance of detecting the shift on any single subgroup; because each new subgroup is another independent opportunity, the shift is caught after about 15 subgroups on average. The chart is slow, not blind, as the average run length below makes precise. We will discuss CUSUM charts and the Western Electric rules, next, as a way to speed up detection.

It is straightforward to see how the type I, \(\alpha\), error rate can be adjusted - simply move the LCL and UCL up and down, as required, to achieve your desired error rates. There is nothing wrong in arbitrarily shifting these limits - more on this later in the section on adjusting limits.

However what happens to the type II error rate as the LCL and UCL bounds are shifted away from the target? Imagine the case where you want to have \(\alpha \rightarrow 0\). As you make the UCL higher and higher, the value for \(\alpha\) drops, but the value for \(\beta\) will also increase, since the control limits have become wider! You cannot simultaneously have low type I and type II error, or as said more colloquially, “there is no free lunch”.

2. Using the average run length (ARL)

The average run length (ARL) is defined as the average number of sequential samples we expect before seeing an out-of-bounds, or out-of-control signal. When the process is on target, this is given by the inverse of \(\alpha\), as \(\text{ARL}_0 = \frac{1}{\alpha}\). Recall for the theoretical distribution we had \(\alpha = 0.0027\), so \(\text{ARL}_0 = 370\). Thus we expect a run of 370 samples between false alarms; this is the in-control ARL, written \(\text{ARL}_0\).

The complementary quantity is the out-of-control ARL, \(\text{ARL}_1 = \frac{1}{1-\beta}\), the average number of subgroups needed to detect a shift that is genuinely present. For the \(0.75\sigma\) shift discussed above (\(n=4\), \(\beta = 0.9332\)), \(\text{ARL}_1 = 1/(1-0.9332) \approx 15\) subgroups; for a \(1\sigma\) shift it is \(1/(1-0.8413) \approx 6\). So the single-subgroup \(\beta\) overstates how blind the chart is: each new subgroup is another chance to detect, and detection compounds over successive samples. A good chart has a large \(\text{ARL}_0\) (rare false alarms) and a small \(\text{ARL}_1\) (fast detection); the two are traded off against each other.

3.4.5. Extensions to the basic Shewhart chart to help monitor stability of the location

The Western Electric rules: we saw above how sluggish the Shewhart chart is in detecting a small shift in the process mean, from \(\mu\) to \(\mu + \Delta\sigma\). The Western Electric rules are an attempt to more rapidly detect a process shift, by raising an alarm when these improbable events occur. The basic chart already implements the primary rule, a single point beyond \(3\sigma\); the three supplementary run rules are added on top of it:

1. Two out of 3 points lie beyond \(2\sigma\) on the same side of the centre line

2. Four out of 5 points lie beyond \(1\sigma\) on the same side of the centre line

3. Eight successive points lie on the same side of the center line

However, an alternative chart, the CUSUM chart is more effective at detecting a shift in the mean. Notice also that each extra rule is another way to signal, so the rules raise sensitivity but shorten the in-control ARL: the four rules together give \(\text{ARL}_0 \approx 92\) rather than 370, meaning more frequent false alarms. Adding still more rules continues this trade-off.

Adding robustness: the phase I derivation of a monitoring chart is iterative. If you find a point that violates the LCL and UCL limits, then the approach is to remove that point, and recompute the LCL and UCL values. That is because the LCL and UCL limits would have been biased up or down by these unusual points \(\overline{x}_k\) points.

This iterative approach can be tiresome with data that has spikes, missing values, outliers, and other problems typical of data pulled from a process database (historian). Robust monitoring charts are procedures to calculate the limits so the LCL and UCL are resistant to the effect of outliers. For example, a robust procedure might use the medians and MAD instead of the mean and standard deviation. An examination of various robust procedures, especially that of the interquartile range, is given in the paper by D. M. Rocke, Robust Control Charts, Technometrics, 31 (2), p 173 - 184, 1989.

Note: do not use robust methods to calculate the values plotted on the charts during phase 2, only use robust methods to calculate the chart limits in phase 1!

Warning limits: it is common to see warning limits on a monitoring chart at \(\pm 2 \sigma\), while the \(\pm 3\sigma\) limits are called the action limits. Real-time computer systems usually use a colour scheme to distinguish between the warning state and the action state. For example, the chart background changes from green, to orange to red as the deviations from target become more severe.

Adjusting the limits: The \(\pm 3\sigma\) limits are not set in stone. Depending on the degree to which the source data obey the assumptions, and the frequency with which spikes and outliers contaminate your data, you may need to adjust your limits, usually wider, to avoid frequent false alarms. Nothing makes a monitoring chart more useless to operators than frequent false alarms (”crying wolf”). However, recall that there is no free lunch: you cannot simultaneously have low type I and type II error.

Changing the subgroup size: It is perhaps a counterintuitive result that increasing the subgroup size, \(n\), leads to a more sensitive detection system for shifts in the mean, because the control limits are pulled in tighter. However, the larger \(n\) also means that it will take longer to see the detection signal as the subgroup mean is averaged over more raw data points. So there is a trade-off between subgroup size and the run length (time to detection of a signal).

3.4.6. Mistakes to avoid

1. Imagine you are monitoring an aspect of the final product’s quality, e.g. viscosity, and you have a product specification that requires that viscosity to be within, say 40 to 60 cP. It is a mistake to place those specification limits on the monitoring chart as a guide when to take action. It is also a mistake to use the required specification limits instead of the LCL and UCL. The monitoring chart is to detect abnormal variation in the process and gives a signal on when to take action, not to inspect for quality specifications. You can certainly have another chart for that, but the process monitoring chart’s limits are intended to monitor process stability, and these Shewhart stability limits are calculated differently. Ideally the specification limits lie beyond the LCL and UCL action limits.

2. Shewhart chart limits were calculated with the assumption of independent subgroups (e.g. subgroup \(i\) has no effect on subgroup \(i+1\)). For a process with mild autocorrelation, averaging \(n\) samples into each subgroup reduces, though does not remove, the relationship between successive subgroup means. However processes with heavy autocorrelation (slow moving processes sampled at a high rate, for example), will have LCL and UCL calculated from equation (2) that will raise false alarms too frequently. In these cases you can widen the limits, or remove the autocorrelation from the signal. More on this in the later section on exponentially weighted moving average (EWMA) charts.

3. Using Shewhart charts on two or more highly correlated quality variables, usually on your final product measurement, can increase your type II (consumer’s risk) dramatically. We will come back to this very important topic in the section on latent variable models, where we will counterintuitively prove that even having individual charts each within their respective limits can result where it is outside the joint limits.